| |
|
[组图]中考数学全真模拟试卷6
|
| 查询数中考复习的详细结果
|
|
1. 8×86=688,这个算式,把乘数的个位数6放在被乘数之首,十位数8放在被乘数之尾,
得688即乘积,还有没有这样的算式?若有,请写出它们。
2.有一些合数分解成质数的积,等式两边的数码的和相等,如:6036=2×2×3×503,6+
0+3+6=2+2+3+5+0+3。数学爱好者史密斯发现493 777 5=3×5×5×65 837,4+9+3+7+7+7+5=3+5+5+6+5+8+3+7,493 777 5恰为史密斯家的电话号码,这个数又是已知的具有上述性质的最大的数。
在10000以内的合数有360个具有这样的性质,请你尽可能多地写出它们。
3.现有四个有理数3,4,-6,10。将这四个数(每个数用且只用一次)进行加、减、乘、
除四则运算,使其结果等于24,其三种本质不同的运算式如下:
(1)__________(2)___________(3)_________
另有四个数3,-5,7,-13,可通过运算式(4)_____________使其结果等于24。
4.某位老师在讲“实数”时,画了一个图(如图),即“以数轴上的单位长线段作一个正方
形,然后以原点O为圆心,正方形的对角线长为半径画弧交 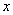 轴于点A”,作这样的图是用来说明_______。
轴于点A”,作这样的图是用来说明_______。
5.用实际例子说明绝对值的几何意义。
6.定义一种运算“ 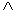 ”,对任何两个正数
”,对任何两个正数 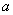 和
和 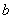 有
有 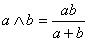 。验证运算“
。验证运算“ 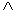 ”是否具有
”是否具有
交换律、结合律、对加法的分配律?即
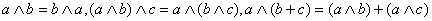 是否成立?请你给出另一种新的运算定义,使其具有交换律、结合律或者对他运算的分配律。
是否成立?请你给出另一种新的运算定义,使其具有交换律、结合律或者对他运算的分配律。
7.已知1, 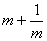 ,2三个数,请你添上一个数,写出一个比例式:__________。
,2三个数,请你添上一个数,写出一个比例式:__________。
8.写出一个只含有字母X的代数式(要求:(1)要使此代数式有意义,字母X必须取全体
正数;(2)此代数式的值恒为负数):______________________。
9.写出两个  的有理化因式。
的有理化因式。
10.在下列括号内填上适当的多项式 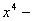 ( )=(
( )=( 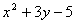 )( )
)( )
11.设Δ是以整数 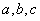 为系数的一元二次方程
为系数的一元二次方程 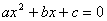 的判别式,能适当地选择
的判别式,能适当地选择
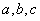 使Δ等于整数1,2,3…,19,20吗?若能,请写出满足题意的
使Δ等于整数1,2,3…,19,20吗?若能,请写出满足题意的 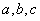 的值。
的值。
12.已知 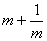 =3,求
=3,求 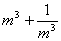 的值。
的值。
13.请你写出一个多项式,使它在实数范围内因式分解,要求所用的方法是“分组分解法”,
且至少有两种不同的分组的方法。请你将分组分解的过程及结果也写下来。
14.举出不是方程的例子。
15.比较方程 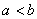 和
和 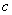 的异同。
的异同。
16.阅读问题与解答,然后回答问题:关于X的方程 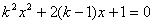 有实数根。(1)求
有实数根。(1)求 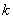 的取值范围;(2)假如这个方程的两个实数根的倒数和的平方等于8,求
的取值范围;(2)假如这个方程的两个实数根的倒数和的平方等于8,求 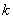 的值。
的值。
17.关于方程的表格: |
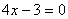
|
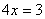
|
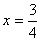
|
|
| |
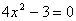
|
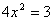
|
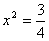
|
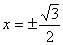
|
| |
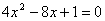
|
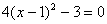
|
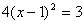
|
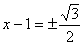
|
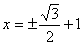
| |
从上面的表格,你可以得到哪些信息或结论?
18.举出可用换元法求解的方程的例子。
19.具体给出整数 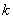 使关于
使关于 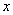 的方程
的方程 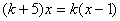 在整数范围内有解。
在整数范围内有解。
20.求作一个关于 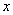 的方程使其一个解
的方程使其一个解 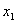 在1与2之间(即1<
在1与2之间(即1< 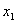 <2
<2
21.方程 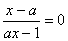 与
与 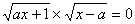 的解有区别,请你指出这些区别并给出两个类
的解有区别,请你指出这些区别并给出两个类
似的方程。
22.某初一学生在做作业时,不慎将墨水打翻,使一道作业题只看到如下字样:“甲、乙两
地相距40千米,摩托车的速度为45千米/小时,运货车的速度为35千米/时,______________?”(横线部分表示被墨水覆盖的若干文字)。请将这道作业题补充完整,并列方程解答。
23.某商场计划拨款9万元从厂家购进50台电视机。已知该厂家生产三种不同型号的电视
机,出厂价分别为:甲种每台1500元,乙种每台2100元,丙种每台2500元。(1)若商场同时购进其中两种不同型号电视机50台,用去9万元,请您研究一下商场的进货方案;(2)若商场销售一台甲种电视机可获利150元,销售一台乙种电视机可获利200元,销售一台丙种电视机可获利250元,在同时购进两种不同型号的方案中,为使销售时获利最多,你选择哪种进货方案;(3)若商场预备用9万元同时购进三种不同型号的电视机50台,请你设计进货方案。
24.已知 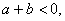 不加任何其他条件,根据不等式的基本性质,你能推出一些什么样的不等式?
不加任何其他条件,根据不等式的基本性质,你能推出一些什么样的不等式?
25.已知 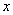 <0,试给实数
<0,试给实数 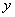 附加限制条件,使不等式
附加限制条件,使不等式 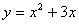 成立。
成立。
26.对于问题“求 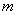 为何值时,不等式
为何值时,不等式 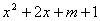 的值恒大于零?”,在不改变题意的前提下,用各种不同的方式叙述该题。
的值恒大于零?”,在不改变题意的前提下,用各种不同的方式叙述该题。
27.写出两个一元一次不等式组,使它的解中含有且只能含有实数-4,0,1,3中的某一个。
28.已知关于 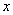 的不等式
的不等式 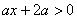 ,下面给出四种说法:
,下面给出四种说法:
(1)该不等式的解为 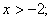 (2)该不等式的解为
(2)该不等式的解为  (3)该不等式无解;
(3)该不等式无解;
(4)该不等式的正确解法是:当 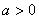 时,
时, 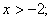 当
当 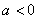 时,
时, 
其中一个错误说法的序号是_______,因为当 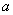 =_________时,该说法的结论不成立。
=_________时,该说法的结论不成立。
29.轻易证实: 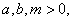 且
且 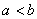 ,则
,则 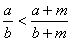
请你给出一个具有实际背景的应用题,验证上述不等式。
30. 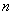 为正整数,请你确定
为正整数,请你确定 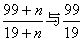 之间的正整数的个数,并使其所对应的正整数
之间的正整数的个数,并使其所对应的正整数 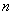 的
的
取值范围之和不小于2008。
31.写出右图相类似的函数解析式,它的图象一段外形如图所示,它通过两个点(1,11),
(2,8)。
32.比较函数  ,
, 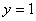 ,
, 
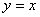 ,
, 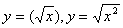 的异同。
的异同。
33.已知一次函数 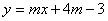 的图象经过第一象限,请给出尽可能多的
的图象经过第一象限,请给出尽可能多的 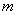 的值并写出
的值并写出
一次函数的表达式。
34.写出两个二次函数,使得它们的和是一次函数。
35.写出一个函数的解析式,并求它的图象和 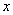 轴所围成图形的面积。
轴所围成图形的面积。
36.记两个函数的解析式分别为 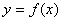 和
和 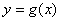 ,A与B为不同时为0且A+B≠0的
,A与B为不同时为0且A+B≠0的
两个实数, 称函数 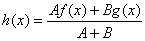 为由函数
为由函数  与函数
与函数  生成的函数。请举例说明由函数
生成的函数。请举例说明由函数  与函数
与函数  生成的函数
生成的函数 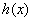 与涵数
与涵数  与函数
与函数  之间一个关系。
之间一个关系。
37.已知二次函数 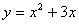 ,请画出其图象并写出你得出的关于图象的结论。
,请画出其图象并写出你得出的关于图象的结论。
38.在等腰三角形ABC中,底边长 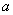 ,底边上的高为变量
,底边上的高为变量 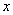 ,请写出关于
,请写出关于 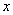 的函数关系。
的函数关系。
39.已知点A(1,2)和B(-2,5),试写出两个二次函数,使它们的图象都经过A、B两
点。
40.已知二次函数 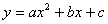 的图象经过点A(
的图象经过点A( 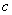 ,0),且关于直线
,0),且关于直线 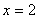 对称,则这
对称,则这
个二次函数的解析式可能是___________(只要求写出一个可能的解析式)。
41.阅读下面文字后,解答问题。有这样一道题目:“已知:二次函数 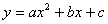 的图象经过点A(0,
的图象经过点A(0, 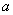 ),B(1,-2)____,求证:这个二次函数图象对称轴是直线
),B(1,-2)____,求证:这个二次函数图象对称轴是直线 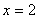 。”题目中的横线部分是一段被墨水污了无法辨认的文字。(1)略(2)请你根据已有的登记处,在原题中的横线上,填加一个适当的条件,把原题补充完整。
。”题目中的横线部分是一段被墨水污了无法辨认的文字。(1)略(2)请你根据已有的登记处,在原题中的横线上,填加一个适当的条件,把原题补充完整。
42.已知抛物线 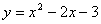 。(1)略。(2)若这条抛物线与
。(1)略。(2)若这条抛物线与 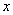 轴的交点从左到右依次为
轴的交点从左到右依次为
A、B,其对称轴与 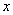 轴相交于点C。设⊙D的直径为BC,⊙A的半径为R,现要使⊙A与⊙D相交,请你写出能符合上述要求的R的任意两个数值,并说明理由。
轴相交于点C。设⊙D的直径为BC,⊙A的半径为R,现要使⊙A与⊙D相交,请你写出能符合上述要求的R的任意两个数值,并说明理由。
43.老师给出一个函数 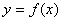 ,甲、乙、丙、丁四位同学各指出这个函数的一个性质:
,甲、乙、丙、丁四位同学各指出这个函数的一个性质:
甲:函数图像不经过第三象限; 乙:函数图像经过第一象限;丙:当 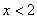 时,
时, 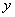 随
随 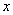 的增大而减小;丁:当
的增大而减小;丁:当 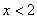 时,
时, 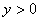 。已知这四个同学叙述都正确,请构造出满足上述所有性质的一个函数:______。
。已知这四个同学叙述都正确,请构造出满足上述所有性质的一个函数:______。
44.已知:如图ΔABC中,AB=AC=10,BC=12,F为BG的中点,D是FC上的一点,过点D
作BC的垂线交AC于点G,交BA的延长线于点E,假如设DC= 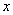 ,则
,则
(1)图中哪些线段(如线段BD可以看成 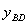 )可以看成是
)可以看成是 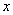 的函数【如
的函数【如 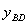 =12-
=12- 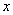 (
( 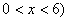 )。请写出其中的四个函数关系式:
)。请写出其中的四个函数关系式:
①________②_______③________④________
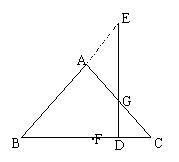 (2)图中哪些图形的面积(如ΔCDG的面积可记作SΔCDG)可以看成是 (2)图中哪些图形的面积(如ΔCDG的面积可记作SΔCDG)可以看成是 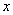 的函数【如SΔCDG=
的函数【如SΔCDG= 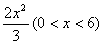 】。请写出另两个函数的解析式。
】。请写出另两个函数的解析式。
|
 (2)图中哪些图形的面积(如ΔCDG的面积可记作SΔCDG)可以看成是
(2)图中哪些图形的面积(如ΔCDG的面积可记作SΔCDG)可以看成是