| 中文域名: 古今中外.com
英文域名:www.1-123.com 丰富实用的教育教学资料 |
| |
| |
| |
|
|
二、填空题: 13. x(xy 2)(xy -2) 14. 1/5 15. 16. 17. 三 18.(2,5)或(4,4) 三、解答题: 19、去分母,得
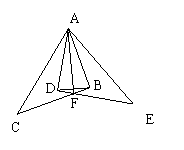
20. 说明:本题共有四个命题,其中命题二、命题三是真命题,命题一、命题四是假命题. 命题一:在△ABC和△DEF中,B、E、C、F在同一直线上, AB=DE,AC = DF,∠ABC=∠DEF。求证:BE=CF 命题二:在△ABC和△DEF中,B、E、C、F在同一直线上,AB=DE,AC = DF,BE=CF。求证:∠ABC=∠DEF 命题三:在△ABC和△DEF中,B、E、C、F在同一直线上,AB=DE,∠ABC=∠DEF, BE=CF。求证: AC = DF 命题四:在△ABC和△DEF中,B、E、C、F在同一直线上,AC = DF,∠ABC=∠DEF,BE=CF。求证: AB=DE 21.解:(1)设P1、P4、P8顺次为3个班考评分的平均数; W1、W4、W8顺次为3个班考评分的中位数; Z1、Z4、Z8顺次为3个班考评分的众数. 则:P1= P4= P8= W1=10(分),W4=8(分),W8=9(分). (Z1=10(分),Z4=8(分),Z8=9(分)). ∴平均数不能反映这3个班的考评结果的差异,而用中位数(或众数)能反映差异, 且W1>W8>W4(Z1>Z8>Z4). (2)(给出一种参考答案)选定: 行为规范:学习成绩:校运动会:艺术获奖:劳动卫生=3:2:3:1:1 设K1、K4、K8顺次为3个班的考评分,则: K1=0.3×10 0.2×10 0.3×6 0.1×10 0.1×7=8.5, K4=0.3×10 0.2×8 0.3×8 0.1×9 0.1×8=8.7, K8=0.3×9 0.2×10 0.3×9 0.1×6 0.1×9=8.9. ∵K8>K4<K1,∴推荐初三(8)班为市级先进班集体的候选班. 22.解:(1)由图象知,当t由0增大到4时,点P由B→C,∴ (2) (3)同理,由图象知CD= ∴图1中图形面积为4×8 2×14=60(cm2) (4)图1中多边形的周长为(14 6)×2= 23. (1)∠EDP=∠EPD或ED=EP或△EDP为等腰三角形 连接OD ∵ED为⊙O切线 ∴∠EDP ∠ODA=90° ∵OA⊥OB ∴∠OPA ∠A=90° ∵OD=OA ∴∠A=∠ODA ∴∠EDP=∠OPA 又∵∠OPA=∠EPD ∴∠EDP=∠EPD ∴EP=ED (2)第⑴题中发现的规律仍然存在,证实思路类似第(1)题. 24.解:(1)连结AC、EF∵太阳光线是平行线∴AC∥EF∴∠ACB=∠EFD ∵∠ABC=∠EDF=90°∴△ABC∽△EDF ∴
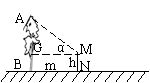
(2)(方法一) 如图MG=BN=m AG=m tanα ∴AB=(m tanα+h)米 (方法二)
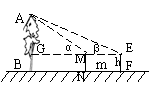 ∴ AG = ∴ AG = 或AB=
25. ∵甲乘上等车的概率为1/3,而乙乘上等车的概率为1/2,∴乙的方案乘上等车的可能性大. 26.解:(1)由对称性易得抛物线顶点坐标为(3,4),用顶点式求得抛物线解析式为y=-(x-3)2 4,即y=-x2 6x-5 (2)因为抛物线对称轴直线x=3垂直平分弦AB,根据垂径定理及其推论易得直线x=3也垂直平分弦DE,易得DE=6,易得△COA≌△BOD,所以OD=OA=1,所以E点坐标为(6,-1),易得直线CE解析式为y= (3)符合条件的点F存在,F1(7.5,0),F2(-7.5,0),F3( CF1、CF2、CF3分别与⊙O’相交,CF4与⊙O’相切。
2006年中考全真模拟试卷(四)参考答案 一、选择题
二、填空题 13、2005 14、1<d<5 15、乙 16、2 17、(-4,3) 18、4 三、解答题 19、解:设梨的单价为x元/千克,苹果的单价为1.5x元千克 30/x - 30/(1.5x)=2.5 解得:x=4 经检验:x=4是原方程的解 ∴x=4,1.5x=6 答:梨和苹果的单价分别为4元/kg和6元/kg。 20、解:设小宝体重为xkg,则妈妈体重为2xkg,爸爸体重为(150-3x)kg x 2x<150-3x x 2x 10>150-3x 解得:231/3 < x < 25
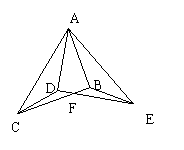 答:小宝的体重范围为大于231/ 答:小宝的体重范围为大于231/21、第一种:连结CD、BE,得:CD=BE ∵△ABC≌△ADE,∴AD=AB,AC=AE ∠CAB=∠EAD ∴∠CAD=∠EAB ∴△ABE≌△ADC
 ∴CD=BE ∴CD=BE
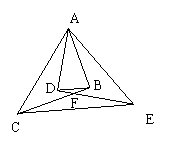
第二种:连结DB、CE得:DB∥CE ∵△ABC≌△ADE,∴AD=AB,∠ABC=∠ADE ∴∠ADB=∠ABD,∴∠BDF=∠FBD 同理:∠FCE=∠FEC ∴∠FCE=∠DBF
 ∴DB∥CE ∴DB∥CE
第三种:连结DB、AF;得AF⊥B D ∵△ABC≌△ADE,∴AD=AB,∠ABC=∠ADE=90° 又AF=AF,∴△ADF≌△ABF ∴∠DAF=∠BAF ∴AF⊥BD
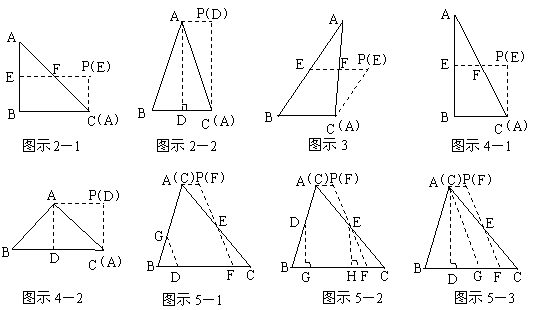
第四种:连结CE、AF;得AF⊥CE ∵△ABC≌△ADE,∴AD=AB,AC=AE ∠ABC=∠ADE=90° 又AF=AF,∴△ADF≌△ABF ∴∠DAF=∠BAF ,∴∠CAF=∠EAF ∴AF⊥BD 22、(1)∵白球的个数为50-1-2-10=37 ∴摸不到奖的概率是: (2)获得10元的奖品只有一种可能即同时摸出两个黄球 ∴获得10元奖品的概率是: 23、⑴ 长方形的长为 24、解:⑴ 方法一:∠B=90°,中位线EF,如图示2-1. 方法二:AB=AC,中线(或高)AD,如图示2-2. ⑵ AB=2BC(或者∠C=90°,∠A=30°),中位线EF,如图示3. ⑶ 方法一:∠B=90°且AB=2BC,中位线EF,如图示4-1. 方法二:AB=AC且∠BAC=90°,中线(或高)AD,如图示4-2. ⑷ 方法一:不妨设∠B>∠C,在BC边上取一点D,作∠GDB=∠B交AB于G,过AC的中点E作EF∥GD交BC于F,则EF为剪切线.如图示5-1. 方法二:不妨设∠B>∠C,分别取AB、AC的中点D、E,过D、E作BC的垂线,G、H为垂足,在HC上截取HF=GB,连结EF,则EF为剪切线.如图示5-2. 方法三:不妨设∠B>∠C,作高AD,在DC上截取DG=DB,连结AG,过AC的中点E作EF∥AG交BC于F,则EF为剪切线.如图示5-2. SHAPE \* MERGEFORMAT
25、解:⑴y=2 0.2x ⑵w=(200-x)(2 0.2x)=-0.2x2 38x 400 ⑶利润Q=w-20x-400 =-0.2x2 38x 400-20x-400 =-0.2x2 18x ∵-b/( ( ∴项点坐标为(45,405) 又∵a=-0.2<0 ∴当存放天数为45天时,可获得最大利润为405元。 26、(1)连结OM,作ON⊥CD于N
∵四边形ABCD是正方形 ∴AC平分∠BCD ∴OM=ON ∴CD与⊙O相切 (2)∵四边形ABCD是正方形 ∴AD=CD=1,∠D=90°,∠ACD=45° ∴AC= ∴NC=OC=OA ∴OC= ∵AC=AO OC= (3)ME=FN,AE=AF 证实:作OG⊥AD,OH⊥AB ∵AC平分∠BAD ∴OG=OH ∴AE=AF ∵AD=AB ∴DF=BE ∵CD、CB与⊙O相切 ∴CM=CN ∵BC=DC ∴BM=DN 又∵∠B=∠D=90° ∴△EBM≌△FDN ∴EM=FN 2006年中考全真模拟试卷(五)参考答案 一、选择题 :
| 题号
| 1
| 2
| 3
| 4
| 5
| 6
| 7
| 8
| 9
| 10
| 11
| 12
| 答案
| B
| A
| C
| C
| C
| D
| C
| B
| D
| C
| A
| A |
二、填空题:
13、x≤ ![]()
14、 ![]()
15、AE=AD或∠B=∠C或∠AEB=∠ADC;
16、-2;
17、65°或115°
18、3n 1
三、解答题
19、解 :设捐款2元的有 ![]()
![]()
![]()
![]()
答:捐款2元的有 15名同学,捐款3元的有12 名同学,
20、(1)平均数=20.5, 众数=18, 中位数=18
(2)合格标准的次数应定为18次较为合适,因为18既为众数也为中位数,且大部份的初中毕业女生都能达到.
(3)0.5-9.5组的频率=(50-26-17-6)/50=0.02
(4)合格人数=30000×41/50=24600
21、(1)略解:∠由矩形的性质可知:Rt△ABC ≌Rt△DEF,AC⊥BD,EF⊥BD。
∵∠A=∠D ,∠ANP=∠DNC
又∵∠D ∠DNC=90O
∴∠A ∠ANP=90O
∴AB⊥ED。
(2)如:△APN ≌△DCN
理由:∵Rt△ABC ≌Rt△DEF
∴AB=BD
又∵PB=BC
∴AP=DC
∴在△APN和△DCN中,
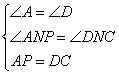
∴ △APN ≌△DCN
22、(1)用列表法来表示所得到的数字之积。
乙
甲
1
2
3
4
5
6
1
1×1=1
2×1=2
3×1=3
4×1=4
5×1=5
6×1=6
2
1×2=2
2×2=4
3×2=6
4×2=8
5×2=10
6×2=12
3
1×3=3
2×3=6
3×3=9
4×3=12
5×3=15
6×3=18
4
1×4=4
2×4=8
3×4=12
4×4=16
5×4=20
6×4=24
(2)由上表可知,两数之积的情况有24种,所以P(数字之积为奇数)= ![]()
23、解法一:过点B作BM⊥AH于M,∴BM∥AF.∴∠ABM=∠BAF=30°.
在△BAM中,AM= ![]() AB=5,BM=5
AB=5,BM=5 ![]() .
.
 过点C作CN⊥AH于N,交BD于K.
过点C作CN⊥AH于N,交BD于K.
在Rt△BCK中,∠CBK=90°-60°=30°
设CK=x,则BK= ![]() x.
x.
在Rt△ACN中,∵∠CAN=90°-45°=45°,
∴AN=NC.∴AM MN=CK KN.
又NM=BK,BM=KN.
∴x 5 ![]() =5
=5 ![]() x.解得x=5.
x.解得x=5.
∵
答:这艘渔船没有进入养殖场危险.
解法二:过点C作CE⊥BD,垂足为E,∴CE∥GB∥FA.
∴∠BCE=∠GBC=60°.∠ACE=∠FAC=45°.
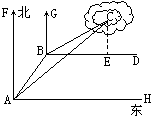 ∴∠BCA=∠BCE-∠ACE=60°-45°=15°.
∴∠BCA=∠BCE-∠ACE=60°-45°=15°.
又∠BAC=∠FAC-∠FAB=45°-30°=15°,
∴∠BCA=∠BAC.∴BC=AB=10.
在Rt△BCE中,CE=BC·cos∠BCE=BC·cos60°=10× ![]() =5(海里).
=5(海里).
∵
答:这艘渔船没有进入养殖场的危险.
24、解:(1)设y1 与x 函数关系式为y1=kx,
把(1,2000)代入上式得k=2000,
所以y1 与x 函数关系式为y1=2000x,
(2)①y与x的函数关系式为 ![]()
②当y=70000时,70000= ![]()
整理得: ![]()
解得: ![]()
25、解(1)重叠部分面积等于 ![]()
(2)等边三角形的边长a至少应为
(3)等边三角形的边长为 ![]()
26、(1)解法一:∵一次函数 ![]()
∴点A的坐标为(4,0)
∵抛物线 ![]()
![]()
![]()
解法二:∵一次函数 ![]()
∴点A的坐标为(4,0)
∵抛物线 ![]()
∴抛物线的对称轴为直线 ![]()
![]()
![]()
(2)解:由抛物线的对称性可知,DO=DA
∴点O在⊙D上,且∠DOA=∠DAO
又由(1)知抛物线的解析式为 ![]()
∴点D的坐标为( ![]()
①当 ![]()
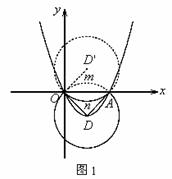
如图1,设⊙D被x轴分得的劣弧为 ![]()
![]()
![]()
∴点D'与点D也关于x轴对称
∵点O在⊙D'上,且⊙D与⊙D'相切
∴点O为切点
∴D'O⊥OD
∴∠DOA=∠D'OA=45°
∴△ADO为等腰直角三角形
![]()
∴点D的纵坐标为 ![]()
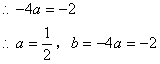
∴抛物线的解析式为 ![]()
②当 ![]()
同理可得: ![]()
抛物线的解析式为 ![]()
综上,⊙D半径的长为 ![]()
![]()
![]()
(3)解答:抛物线在x轴上方的部分上存在点P,使得 ![]()
设点P的坐标为(x,y),且y>0
①当点P在抛物线 ![]()
∵点B是⊙D的优弧上的一点
![]()
![]()
过点P作PE⊥x轴于点E
由 
∴点P的坐标为 ![]()
②当点P在抛物线 ![]()
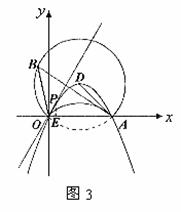
同理可得, ![]()
由 
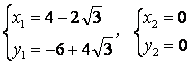
∴点P的坐标为 ![]()
综上,存在满足条件的点P,点P的坐标为
![]()
![]()
2006年中考全真模拟试卷(六)参考答案
一、选择题 :
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
C
B
D
B
D
C
A
C
A
C
B
二、填空题:
13、3 ;
14、3 ;
15、2π ;
16、4 ;
17、 ![]()
18、 ![]()
三、解答题
19、、解:原式 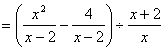
![]()
![]()
![]()
![]()
20、如:(1)连结AF,
(2)猜想AF=AE
(3)证法一:
连结AC,交BD于O
![]()
![]()
![]()
![]()
![]()
证法二: ![]()
![]()
![]()
![]()
在 ![]()
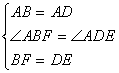
![]()
![]()
21、解:(1)①仅画小明已先抽到黑桃4(不放回)时的树状图 ②小华抽出的牌的牌面数字比4大的概率是 ![]()
(2)这个游戏不公平。小明胜的情况共有5种,即(4,2),(5,2),(5,2),(5,4),(5,4),故小明获胜的概率为 ![]()
![]()
![]()
22、(1)
平均数
众数
方差
甲
6
乙
7
8
(2)如:选甲运动员参赛理由:
i从平均数看两人平均成绩一样;
ii从方差看,甲的方差小于乙的方差,甲的成绩比乙稳定.
故选择甲运动员参赛.
或者选乙运动员参赛,理由:
i从众数看,乙比甲的成绩好;
ii从发展趋势看,乙比甲潜能更大.
故选择乙运动员参赛.
23、解:(1) 
(2)如图1-1或如图1-2或如图1-3或如图1-4等,图形正确。
 |
24、解:(1)设安排甲种货车x辆,则安排乙种货车(10-x)辆,依题意,得
![]()
解这个不等式组,得 ![]()
![]()
![]() 是整数,
是整数, ![]() x可取5、6、7,
x可取5、6、7,
既安排甲、乙两种货车有三种方案:
甲种货车5辆,乙种货车5辆;
甲种货车6辆,乙种货车4辆;
甲种货车7辆,乙种货车3辆;
(2)方法一:由于甲种货车的运费高于乙种货车的运费,两种货车共10辆,
所以当甲种货车的数量越少时,总运费就越少,故该果农应
选择① 运费最少,最少运费是16500元;
方法二:方案①需要运费
2000×5 1300×5=16500(元)
方案②需要运费
2000×6 1300×4=17200(元)
方案③需要运费
2000×7 1300×3=17900(元)
![]() 该果农应选择① 运费最少,最少运费是16500元;
该果农应选择① 运费最少,最少运费是16500元;
25、(1)在上述旋转过程中,BH=CK,四边形CHGK的面积不变.
证实:连结CG
∵△ABC为等腰直角三角形,O(G)为其斜边中点
∴CG=BG,CG⊥AB.
∴∠ACG=∠B=45°.
∵∠BGH与∠CGK均为旋转角,
∴∠BGH=∠CGK.
∴△BGH≌△CGK.
∴BH=CK,S△BGH=S△CGK.
∴S四边形CHGK=S△CHG S△CGK=S△CHG S△BGH= ![]()
![]()
![]()
即:S四边形CHGK的面积为4,是一个定值,在旋转过程中没有变化.
(2)∵AC=BC=4,BH= ![]()
∴CH=4- ![]()
![]()
|
H |
|
A |
|
G(O) |
|
E |
|
C |
|
B |
|
F |
|
α |
|
K |
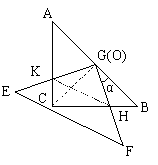 由S△GHK=S四边形CHGK-S△CHK,
由S△GHK=S四边形CHGK-S△CHK,
得 ![]()
![]()
∴ ![]()
∵0°<α<90°,
∴0< ![]()
(3)存在.
根据题意,得 ![]()
解这个方程,得 ![]()
即:当 ![]()
![]()
![]()
26、⑴依题意得有 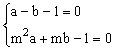
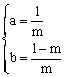
∴抛物线的解析式为: ![]()
⑵∵ ![]()
![]()
![]()
∵ ![]()
![]()
![]()
又∵ ![]()
![]()
|
M |
|
B |
|
C |
|
A |
|
O |
|
x |
|
y |
|
P |
|
D |
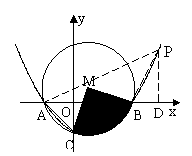 ⑶如图,由抛物线的对称性可知,若抛物线上存在点P, 使得以A、B、P为顶点的三角形与△ABC相似,则P关于对称轴的对称点P’也符合题惫,即P、P’对应的m值相同.下面以点P在对称轴右侧进行分析:
⑶如图,由抛物线的对称性可知,若抛物线上存在点P, 使得以A、B、P为顶点的三角形与△ABC相似,则P关于对称轴的对称点P’也符合题惫,即P、P’对应的m值相同.下面以点P在对称轴右侧进行分析:
情形一:如图,ΔABC∽△APB
则 ![]()
![]()
过点P作 ![]()
![]()
若点P在抛物线上,
则有 ![]()
即 ![]()
![]()
![]()
∴ ![]()
![]()
![]()
此时 ![]()
又由 ![]()
![]()
由①、②有 ![]()
整理得: ![]()
![]()
2006年中考全真模拟试卷(七)参考答案
一、选择题 :
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
D
B
B
D
D
B
C
B
A
A
A
二、填空题:
13、1 ;
14、后面、上面、左面 ;
15、1375元 ;
16、5/2 ;
17、< ;
18、75O或15O
三、解答题
19、解:原式=
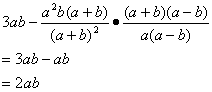
当 ![]()
原式= ![]()
20、 (1) 不公平,因为小明获胜的概率为1/3,小于小刚获胜的概率2/3。(利用树状图说明) (2) 修改方案不唯一,符合要求即可.
21、解:(1)提示: 充分利用格点画图 ;
(2)A2(5,2);B1(-4,-5).
22、(1)获得圆珠笔的概率为: ![]()
![]()
在一个不透明的箱子里放进360个除标号不同外,其他均一样的乒乓球,其中一个标“特”、10个标“1”、30个标“2”、90个标“3”、其余不标数字,摸出标有哪个奖次的乒乓球,则获相应等级的奖品。(本方案仅供参考)
23、解:(1)假如①②③,那么④⑤
证实:如图,延长AE交BC的延长线于F
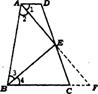 ∵AD∥BC ∴∠1=∠F
∵AD∥BC ∴∠1=∠F
又∵∠AED=∠CEF,DE=EC∴△ADE≌△FCE
∴AD=CF,AE=EF
∵∠l=∠F,∠1=∠2.∠2=∠F
∴AB=BF∴∠3=∠4
∴AD BC=CF BC=BF=AB
(说明:其它真命题的证实可参照上述过程相应给分)
(2)假如①②④,那么③⑤
假如①③④,那么②⑤
假如①③⑤,那么②④
(3)若(1)(2)中四个命题含假命题(“假如②③④,那么①⑤’’),则不加分;若(3)中含假命题,也不加分.
24、解:⑴设 ![]()
∴ ![]()
∴ ![]()
|
O |
|
40 |
|
60 |
|
100 |
|
120 |
|
80 |
|
x(元) |
|
y(万元) |
 ⑵
⑵ ∴当 ![]()
⑶令 ![]()
![]()
![]()
解得: ![]()
![]()
由图象可知,要使年获利不低于40万元,销售单价应在80元到120元之间.
又因为销售单价越低,销售量越大,
所以要使销售量最大,又要使年获利不低于40万元,销售单价应定为80元.
25、解:(1)连结AD,不难求得A(1,2 ![]()
OE= ![]()
![]()
(2)因为抛物线y= ![]()
由待定系数法得:c= ![]()
![]()
抛物线的解析式为y= ![]()
(3)大家记得这样一个常识吗?
“牵牛从点A出发,到河边l喝水,再到点B处吃草,走哪条路径最短?”即确定l上的点P
方法是作点A关于l的对称点A',连结A'B与l的交点P即为所求.
|
A |
|
B |
|
l |
 |
本题中的AC就是“河”,B、D分别为“出发点”和“草地”。
|
A |
|
B |
|
C |
|
O |
|
D |
|
E |
|
y |
|
x |
|
P |
|
D' |
|
F |
|
G |
 由引例并证实后,得先作点D关于AC的对称点D',
由引例并证实后,得先作点D关于AC的对称点D',
连结BD'交AC于点P,则PB与PD的和取最小值,
即△PBD的周长L取最小值。
不难求得∠D'DC=30º
DF= ![]()
![]()
求得点D'的坐标为(4, ![]()
直线BD'的解析式为: ![]()
![]()
直线AC的解析式为: ![]()
求直线BD'与AC的交点可得点P的坐标( ![]()
![]()
此时BD'= ![]()
![]()
![]()
所以△PBD的最小周长L为2 ![]()
把点P的坐标代入y= ![]()
26、解:(1)由 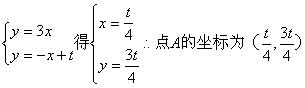
由 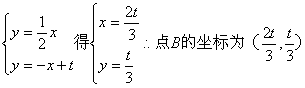
所以 ![]()
(2)由(1)知:点C的坐标为( ![]()
![]()
![]()
(1) 由(1)(2)可知,正方形ABCD的边长
CB= ![]()
(2) 设直线PD的解析式为y=k1x b,由(1)知:
点D的坐标为 ![]()

由 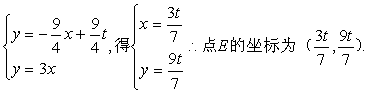
所以 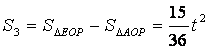
2006年中考全真模拟试卷(八)参考答案
一、选择题 :
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
C
B
D
C
B
C
D
D
C
A
B
二、填空题:
13、3 ;
14、-4或2 ;
15、 ![]()
16、π ;
17、40 ;
18、 ![]()
三、解答题
19、⑴ 一万名学生的竞赛成绩, 500 ⑵ 0.26 ⑶ 第3小组 ⑷ b=10
20、解:如图,由题意知:四边形ACED是矩形
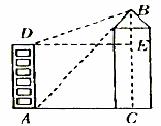
![]()
![]()
设 ![]()
在 ![]()
![]()
在 ![]()
![]()
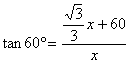
![]()
![]()
![]()
答:大厦的高度BC为
21、(1)计分方案如下表:
n(次)
1
2
3
4
5
6
7
8
M(分)
8
7
6
5
4
3
2
1
(用公式或语言表述正确,同样给分.)
(2) 根据以上方案计算得6局比赛,甲共得24分,乙共得分23分,
所以甲在这次比赛中获胜 .
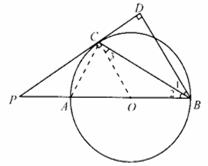 22、证实:(1)连结OC。
22、证实:(1)连结OC。
∵PD切⊙O于点C,
又∵BD⊥PD,
∴OC∥BD。
∴∠1=∠3。
又∵OC=OB,
∴∠2=∠3。
∴∠1=∠2,即BC平分∠PBD。
(2)连结AC。
∵AB是⊙O的直径,
∴∠ACB=90°。
又∵BD⊥PD,
∴∠ACB=∠CDB=90°
又∵∠1=∠2,
∴△ABC∽△CBD
∴ ![]()
23.⑴ ![]()
当x1=5时y1=30, 当x2=5时y2=100/3, ∴第三十分钟时学生的注重力更集中.
⑵ 当y1=36时x1=8 , 当y2=36时x2= ![]()
![]()
24、解:设这个学校选派值勤学生 ![]()
![]()
根据题意得: 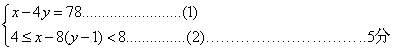
将方程(1)代入不等式(2), ![]()
整理得:19.5< ![]()
根据题意 ![]()
![]()
答:学校派出的是158名学生,分到了20个交通路口安排值勤.
25、(Ⅰ) 证实∵∠A=60O,∠A=2∠B,∴∠C=90O
∴ ![]()
于是, 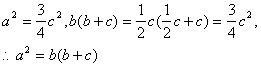
(Ⅱ)仍然成立。
证实:如图,延长BA至点D,使AD=AC=b,连结CD,
则△ACD为等腰三角形。
∵∠BAC为△ACD的一个外角,
∴∠BAC=2∠D。
由已知,∠BAC=2∠B
∴∠B=∠D
∴△CBD为等腰三角形。
又∠D为△ACD和△CBD的一个公共角,
∴ △ ACD∽ △ CBD。
∴ ![]()
∴ ![]()
(Ⅲ)若△ABC是倍角三角形,由∠A =2∠B,应有 ![]()
当a>c>b时,设a=n 1,b=n-1,c=n.(n为大于1的正整数)
代入 ![]()
有a=6,b=4,c=5,可以证实这个三角形中,∠A =2∠B。
当c>a>b及a>b>c时,
均不存在三条边长恰为三个连续正整数的倍角三角形。
∴边长为4,5,6的三角形为所求。
26、(1)∵O、C两点的坐标分别为O(0,0),C(8,6)。
设OC的解析式为y=kx b;
将两点坐标代入得:k= ![]()
![]()
∵抛物线过O、A、C三点,这三点的坐标分别为(0,0)(18,0)(8,6)
∵因为A、O是x轴上的两点,设抛物线的解析式为y=a(x-0)(x-18)
再将C(8,6)代入得: ![]()
(2)D(10,6)
(3)当Q在OC上运动时,可设Q(m, ![]()
依题意有: ![]()
∴ ![]()
当Q在BC时,Q点所走的路程为2t
∵OC=10,CQ=2t-10,
∴Q点的横坐标为2t-10 8=2t-2 ∴Q(2t-2,6)(5≤t≤10)
(4)梯形OABC的周长为44,当Q点在OC上时,P运动的路程为t,则Q运动的路程为(22-t)
△OPQ中,OP边上的高为:(22-t)× ![]()
∴ ![]()
依题意有: ![]()
方程无解,所以这样的t不存在。
当Q在BC上时,Q走过的路程为(22-t)。
∴CQ的长为22-t-10=12-t,
∴ ![]()
∴这样的t值也不存在
综上所述,不存在这样的t值,使得P、Q两点同时平分梯形的周长和面积。
| |