中文域名: 古今中外.com
英文域名：www.1-123.com 丰富实用的教育教学资料
|
|
| 中文域名: 古今中外.com
英文域名：www.1-123.com 丰富实用的教育教学资料 |
| |
| |
| |
|
|
二、填空题（本题共5小题，每小题3分，共15分）
| 题号
| 11
| 12
| 13
| 14
| 15
| 答案
| 3
| X(x 3)(x－3)
| 1.1m
| EQ f(1,6)
|
|
三、解答下列各题（本题共4小题，每小题6分，共24分，写出解题过程。）
16、解：原式＝4－8×0.125 1 1＝5
17、解：① ②得 8x=8→ x=1
把x=1代入①得 y= EQ f(2,3)
∴原方程组的解是 
18、解：原式＝ 
当x=2006时，原式＝2006－6＝2000
19、画图如下：
|
A |
|
B |
|
|
A |
|
B |
|
四、解答题（本题共2小题，每小题7分，共14分）
20、⑴80，80，两班都一样。
⑵70，90，二(2)班较优。
|
⑶二(1)班成绩波动较大，二(2)班成绩比较稳定。
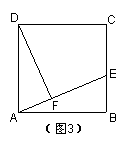
21、解：过点B作BG⊥AE，垂足为G，点G即为所求的点.
理由是：∵DF⊥AE BG⊥AE
∴∠DFA＝∠AGB＝90°∵ABCD是正方形
∴∠ADF ∠DAF＝90°，∠DAF ∠BAG＝90°
∴∠ADF＝∠BAG
又DA＝AB
∴△ABG≌△DAF （AAS）
五、解答题（本题共2小题，每小题8分，共16分）
|
E |
22、解：① 
② 由①得 
当y=106000时，有 106000=19x－8000
解这个方程得 x=6000
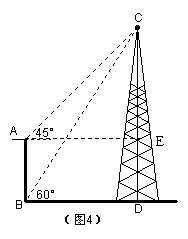
23、解：如图，过点A作AE⊥CD于E，则有四边形ABDE是矩形，
设CE=x m，则CD=(x 20) m
∵∠CAE=45°=∠ACE ∴AE=CE=BD=x
在Rt△BCD中， 
即 EQ f(x 20,x) = EQ r(3)
解这个方程得x=10( EQ r(3) 1) m
|
E |
答：塔高CD为10( EQ r(3) 1) m
六、（本题满分10分）
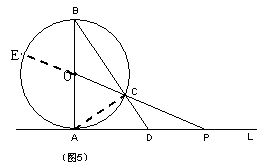
24、解：延长PO交⊙O于E，连结AC.
⑴∵PA切⊙O于A ∴PA2=PC·PE
即42=PC(PC 6)
解之得PC=2（只取正值）
⑵∵△PAO∽△BAD
∴∠APO＝∠ABD
∵OB＝OC
∴∠ABD＝∠OCB
∴∠AOP＝∠ABD ∠OCB＝2∠ABD＝2∠APO
∵PA切⊙O于A
∴∠PAO＝90° ∴∠AOP ∠APO＝90°
即 3∠APO＝90°→∠APO＝30°
七、（本题满分11分）
25、解：⑴设点A（x，y）
∵S△AOB＝4→ EQ f(1,2) xy=4 → y= EQ f(8,x)
⑵把A（x，4）代入y= EQ f(8,x) 得x= 2，∴A（2，4）
∵△APB∽△AOB
① 点P在x轴的正半轴时，且当∠OAB＝∠PAB，则 EQ f(PB,OB) = EQ f(AB,AB) =1 ∴PB＝2，∴P（4，0）
又当∠OAB＝∠APB时，则 EQ f(AB,BP) = EQ f(OB,AB) = EQ f(2,4) = EQ f(1,2) ，∴BP＝8，∴P（10，0）
②当点P在x轴的负半轴时，且当∠OAB=∠APB，则 EQ f(AB,BP) = EQ f(OB,AB) = EQ f(2,4) = EQ f(1,2) ,
∴BP=8，∴P（－6，0）
⑶、①当点P在x轴的负半轴时，即过P、O、A三点坐标分别为
P（－6，0），O（0，0），A（2，4）
设抛物线为y=ax2 bx c，把以上三点分别代入得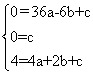 
解这个方程组得 
该抛物线是由抛物线y= EQ f(1,4) x2先向左平移3个单位，然后再向下平移 EQ f(9,4) 个单位而得到。
② 当点P在x轴的正半轴时，过P、O、A三点的抛物线，它的开口是向下，
而抛物线y= EQ f(1,4) x2开口是向上，所以不可能经过平移得到。
| |
