|
热点6 函数图象的画法与解读
(时间:100分钟 总分:100分)
一、选择题(本大题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一个是符合题目要求的)
1.如图是某市一天的气温随时间变化的图象,那么这天( )
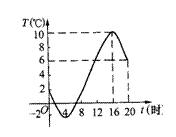 A.最高气温是10℃,最低气温是2℃; A.最高气温是10℃,最低气温是2℃;
B.最高气温是6℃,最低气温是2℃
C.最高气温是10℃,最低气温是-2℃;
D.最高气温是6℃,最低气温是-2℃
2.一根蜡烛原长20cm,点燃后每小时燃烧5cm,则燃烧的速度v(cm/h)与燃烧的时间t(h)的关系用图象表示为( )
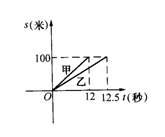 3.甲、乙二人在一次赛跑中,路程s与时间t的关系如图所示,从图中可以看出,下列结论错误的是( ) 3.甲、乙二人在一次赛跑中,路程s与时间t的关系如图所示,从图中可以看出,下列结论错误的是( )
A.这是一次100米赛跑; B.甲比乙先到达终点
C.乙跑完全程需12.5秒; D.甲的速度是8米/秒
4.已知直线y=ax b经过一、二、四象限,则下列结论正确的是( )
A.a>0,b>0;B.a>0,b<0; C.a<0,b>0;D.a<0,b<0
5.图8-4所示图形中,表示函数y=mx n与正比例函数y=mnx(mn≠0)图象的是( )

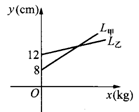
6.如图,L甲、L乙分别是甲、乙两弹簧的长y(cm)与所挂物体质量x(kg)之间的函数关系的图象,设甲弹簧每挂1kg物体伸长的长度为k甲cm,乙弹簧每挂1kg物体伸长的长度为k乙cm,则k甲与k乙的关系是( )
A.k甲>k乙 B.k甲=k乙 C.k甲<k乙 D.不能确定
(第6题) (第7题) (第8题)
7.二次函数y=ax2 bx c(a≠0)的图象如图所示,下列结论:①c<0,②b>0,③4a 2b c>0,④(a c)2<b2.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
8.已知一次函数y=kx b的图象(如图),当x<0时,y的取值范围是( )
A.y>0 B.y<0 C.-2<y<0 D.y<-2
9.下图中阴影部分的面积与算式│- 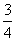 │ (
│ ( 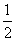 )2 2-1的结果相同的是( )
)2 2-1的结果相同的是( )
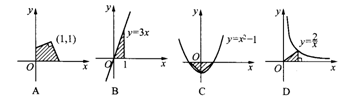
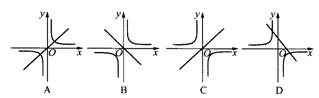
10.已知a为常数,则函数y1=ax,y2= 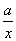 的图象大致是( )
的图象大致是( )
二、填空题(本大题共8小题,每小题3分,共24分)
11.如图,点P是反比例函数y=  上的任意一点,PD⊥x轴于点D,则△POD的面积是__________.
上的任意一点,PD⊥x轴于点D,则△POD的面积是__________.
  
(第11题) (第12题) (第13题)
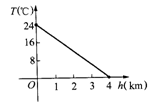
12.在空中,自地面算起,每升高1km,气温会下降若干摄氏度(℃),某地空中气温T(℃)与高度h(cm)间的函数图象如图所示,观察图象可知:地面温度为________℃,当高度为_______km时,气温为0℃.
13.小明同学骑自行车去郊外春游,如图表示他离家的距离y(千米)与所用时间x(时)之间关系的函数图象,请根据图象回答下列问题:
(1)小明到达离家最远的地方用了_______小时;(2)明在途中休息了________小时.
(3)小明出发________小时离家12千米.
14.已知二次函数y1=ax2 bx c(a≠0)与一次函数y2=kx b(k≠0)的图象相交于点A(-2,4),B(8,2),如图所示,则能使y1>y2成立的x的取值范围是_________.
 
(第14题) (第15题)
15.在某一电路中,电源电压U保持不变,电流I(A)与电阻R(Ω)之间的函数图象如图所示.I与R的函数关系式为:___________.
16.结合图象回答:当电路中的电流不得超过12A时,电路中电阻R的取值范围是___________.
三、解答题(本大题共46分,19~23题每题6分,24题、25题每题8分.解答题应写出文字说明、证实过程或演算步骤)
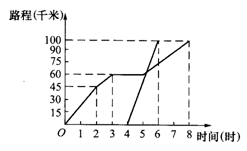
17.甲、乙两人(甲骑自行车,乙骑摩托车)从A城出发到B城旅行,如图表示甲、乙两人离开A城的路程与时间的关系,根据图象你能得到甲、乙两人旅行的哪些信息?(答题要求:至少提供4条信息,如由图象可知A、B两地相距100千米)
18.已知二次函数y=-2x2 8x-6.
(1)用配方法求这个二次函数图象的顶点坐标和对称轴.
(2)画出这个函数的大致图象,指出函数值不小于0时x的取值范围.
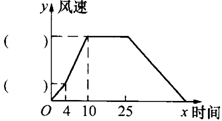
19.某气象研究中心观测一场沙尘暴从发生到结束的全过程,开始时,风速平均每小时增加2千米,4小时后,沙尘暴经过开阔的荒漠地,风速平均每小时增加4千米,一段时间后,风速保持不变,当沙尘暴碰到绿色植被时,其风速每小时减少1千米,最终停止.观察图,回答问题.
(1)在图中( )内填上相应的数字.
(2)沙尘暴从发生到结束,共经过多少小时.
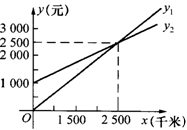
20.某单位急需用车,但又不预备买车,他们预备和一个体车主和一国营出租车公司其中的一家签订租车合同,该汽车每月行驶x千米,应付给个体车主的费用为y1元,应给出租车公司的费用为y2元,y1、y2分别关于x的函数图象如图8-17,观察图象回答下列问题:
(1)每月行驶的路程在什么范围时,租国营公司的车合算.
(2)假如这家单位估计每月行驶的路程为2 300千米,那么这家单位租哪家的车合算?
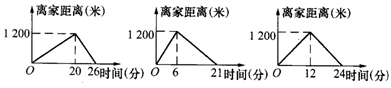
21.小刚的爸爸、爷爷同时从家中出发到达同一目的地后都立即返回,小刚去时骑自行车,返回时步行,爷爷去时步行,返回时骑自行车,爸爸往返都是步行,三人步行的速度不等,小刚与爷爷骑自行车的速度相等,每个人离家的距离与行走的时间关系分别是图中的一个,问:
(1)小刚、爸爸、爷爷往返各用了多少分钟?
(2)他们三人步行的速度分别是多少?
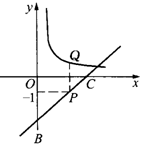
22.如图,点P在经过点B(0,-2),C(4,0)的直线上,且纵坐标为-1,Q点在y=  的图象上,若PQ∥y轴,求Q点的坐标.
的图象上,若PQ∥y轴,求Q点的坐标.
23.已知抛物线y=a(x-t-1)2 t2(a、t是常数,a≠0,t≠0)的顶点是A,抛物线y=x2-2x 1的顶点是B(如图),
(1)判定点A是否在抛物线y=x2-2x 1上,为什么?
(2)假如抛物线y=a(x-t-1)2 t2经过点B,
①求a的值.
②这条抛物线与x轴的两个交点和它的顶点A能否构成直角三角形?若能,求出t的值,若不能,请说明理由.

答案:
一、选择题
1.C 2.A 3.D 4.C 5.A 6.A 7.C 8.D 9.B 10.A
二、填空题
11.1 12.24,4 13.3; 2; 0.8. 14.x<-2或x>8 15.I=  16.R≥3Ω
16.R≥3Ω
三、解答题
17.①乙从A城到B城花了2个小时,②乙的速度为50千米/时,③甲在途中休息过,④甲前3小时走了60千米.
18.解:(1)y=-2x2 8x-6=-2(x2-4x 3)=-2(x-2)2 2,
故顶点坐标为(2,2),对称轴为x=2.
(2)图略.1≤x≤3.
19.解:(1)8,32.(2)25 32=57(时).
20.解:(1)x>2 500千米.(2)租个体车.
21.解:(1)小刚用了21分钟,爸爸用了24分钟,爷爷用了26分钟.
(2)小刚: 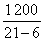 =80(米/秒) 爷爷:
=80(米/秒) 爷爷: 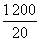 =60(米/分).
=60(米/分).
爸爸:  =100(米/秒)
=100(米/秒)
22.解:设直线BC为y=kx b,将(0,-2),(4,0)代入y=kx b中
有  解得
解得 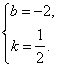
故y= 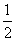 x-2,令y=-1得x=2,故P点的坐标为(2,-1).
x-2,令y=-1得x=2,故P点的坐标为(2,-1).
由于PQ∥y轴,所以Q点的横坐标为2,x=2时,y=  .
.
所以点Q的坐标为(2,  ).
).
23.解:(1)点A的坐标为(t 1,t2)代入y=x2-2x 1中,(t 1)2-2(t 1) 1=t2成立,故点A在y=x2-2x 1上.
(2)①点B的坐标为(1,0),
将(1,0)代入y=a(x-t-1)2 t2中,有0=at2 t2,解得a=-1.
②能够成直角三角形.
设此抛物线与x轴的一个交点为B,另一个交点为C,令y=0,得x1=1,x2=2t 1.
故点B点C的坐标分别是(1,0)、(2t 1,0)
由抛物线的对称性可知,△ABC为等腰三角形.
过点A作AD⊥x轴,垂足为D,则AD=BD.
当点C在点B左边时,t2=1-(t 1)解得t=-1或t=0(舍去);
当点C在点D右边时,t2=(t 1)-1,解得t=1或t=0(舍去);
故t=±1时,抛物线y=-(x-t-1)2 t2和x轴的两个交点与顶点A构成直角三角形.
|