|
高三理科数学上学期期末考试题
注重事项:本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,本试卷满分150分。考试时间120分钟。
http://www.mathedu.cn中国数学教育网
第Ⅰ卷(选择题 共60分)
一、选择题(本大题共12小题,每小匙分,共60分。在每小题的四个选项中,只有一项是符合题目要求的,请将正确选项填在题后括号内。)
1、设全集U=R,A={x| eq \f(1,x)<0},则ðUA等于 ( )
A、{x| eq \f(1,x)>0} B、{x|x>0} C、{x|x≥0} D、{x| eq \f(1,x)≥0}
2.在数列  中,
中, 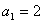 ,
, 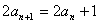 ,则
,则 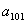 的值为 ( )
的值为 ( )
A 49 B 50 C 51 D 52
3、假如直线l过点P(1,2),且l不经过第四象限,那么l的斜率的取值范围是 ( )
A、[0,2] B、[0,1] C、[0, eq \f(1,2)] D、[- eq \f(1,2),0]
4、在(1 x) (1 x)2 (1 x)3 … (1 x)6展开式中,x2项的系数是 ( )
A、33 B、34 C、35 D、36
5、棱长为1的正四面体,某顶点到其相对面的距离是 ( )
A、 eq \f(\r(,5),3) B、 eq \f(\r(,6),3) C、 eq \f(\r(,2),3) D、 eq \f(\r(,3),3)
6.对于两条直线a,b和平面  ,若
,若 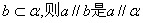 的 ( )
的 ( )
A.充分但不必要条件 B.必要但不充分条件
C.充要条件 D.既不充分又不必要条件
7.随机变量 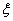 服从正态分布
服从正态分布  ,则
,则 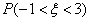 =( )(
=( )( 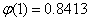 )
)
A.0.8413 B.0.6826 C.0.1587 D.0.3174
8.若把一个函数的图象按 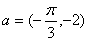 平移后,得到函数
平移后,得到函数  的图象,则原图象的函数解析式是 ( )
的图象,则原图象的函数解析式是 ( )
A. 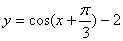 B.
B. 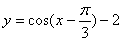
C. 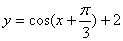 D.
D. 
9、从6人中选4人分别到A、B、C、D四个城市游览,要求每个城市有1人游览,每人只游览一个城市,且这6人中,甲、乙不去A城市游览,则不同的选择方案为 ( )
A、96种 B、144种 C、196种 D、240种
10.设O在△ABC内部,且 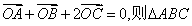 的面积与
的面积与 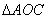 的面积之比为 ( ) A.3 B.4 C.5 D.6
的面积之比为 ( ) A.3 B.4 C.5 D.6
11、已知函数f(x)=2x的反函数为f-–1(x),若f-–1(a) f-–1(b)=4,则 eq \f(1,a) eq \f(1,b)的最小值为 ( )
A、 eq \f(1,2) B、 eq \f(1,3) C、 eq \f(1,4) D、1
12、过抛物线y= 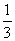
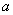 x2(
x2( 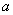 >0)焦点F作一直线交抛物线于P、Q两点,若线段PF、FQ的长度分别为
>0)焦点F作一直线交抛物线于P、Q两点,若线段PF、FQ的长度分别为 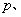
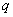 ,则
,则 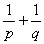 等于 ( )
等于 ( )
A. 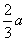 B.
B. 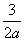 C.
C. 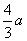 D.
D. 
第Ⅱ卷(非选择题,共90分)
二、填空题(本大题共4小题,每小题4分,共16分,把正确答案填在题中的横线上)
13.已知函数f(x) = 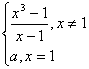 ,若函数f(x)在R上连续,则a=__________
,若函数f(x)在R上连续,则a=__________
14.已知tan(α- EQ \F(π,4))= EQ \F(1,4),则 EQ \F(cosα+sinα,cosα-sinα)=____________
15、已知变量x、y满足约束条件 eq \b\lc\{ (\a\al (x-y 2≤0,x≥1,x y-7≤0)) ,则 eq \f(y,x)的取值范围是_________
16、若函数 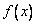 是定义在实数集上的奇函数,且
是定义在实数集上的奇函数,且 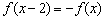 ,给出下列结论:
,给出下列结论:
①  ;②
;② 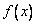 以4为周期;③
以4为周期;③ 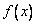 的图象关于
的图象关于 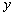 轴对称;④
轴对称;④ 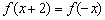 .
.
这些结论中正确结论的序号是 。
三、解答题(本大题共6小题,共74分,解答应写出文字说明、证实过程或演算步骤)
17、(本小题满分12分)已知函数f(x)=(sinx-cosx)sinx (3cosx-sinx)cosx,x∈R
(1)求f(x)的最小正周期;(2)当x∈[0, eq \f(π,4)]时,求f(x)的最大值和最小值。
18、(本小题满分12分)厂家在产品出厂前,需对产品做检验,厂家将一批产品发给商家时,商家按合同规定也需随机抽取一定数量的产品做检验,以决定是否接收这批产品.
(Ⅰ)若厂家库房中的每件产品合格的概率为0.8,从中任意取出4件进行检验.求至少有1件是合格品的概率;
(Ⅱ)若厂家发给商家20件产品,其中有3件不合格,按合同规定该商家从中任取2件,都进行检验,只有2件都合格时才接收这批产品,否则拒收.求该商家可能检验出不合格产品数 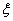 的分布列及期望
的分布列及期望 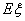 ,并求该商家拒收这批产品的概率.
,并求该商家拒收这批产品的概率.
 19、(本小题满分12分) 19、(本小题满分12分)
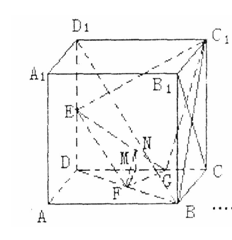
已知在正方体ABCD-A1B1C1D1中,E、F分别是D1D、BD的中点,G在棱CD上,且CG= eq \f(1,4)CD。
(1)求证:EF⊥B1C
(2)求二面角F-EG-C1的大小
20.(本小题满分12分)设各项均为正数的数列 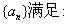
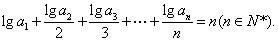
(1)写出 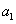 、
、 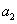 、
、 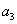 ,并求
,并求  的通项公式;
的通项公式;
(2)设数列 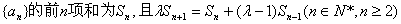 ,求实数
,求实数  的值。
的值。
21.(本小题满分12分)已知函数  (a为常数).
(a为常数).
(1)假如对任意  恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(2)设实数  满足:
满足:  中的某一个数恰好等于a,且另两个恰为方程
中的某一个数恰好等于a,且另两个恰为方程 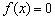 的两实根,判定①
的两实根,判定① 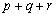 ,②
,② 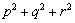 ,③
,③ 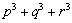 是否为定值?若是定值请求出:若不是定值,请把不是定值的表示为函数
是否为定值?若是定值请求出:若不是定值,请把不是定值的表示为函数  ,并求
,并求  的最小值;
的最小值;
22.(本小题满分14分)已知直线 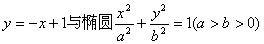 相交于A、B两点,且线段AB的中点在直线
相交于A、B两点,且线段AB的中点在直线 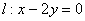 上。
上。
(1)求此椭圆的离心率;
(2)若椭圆的右焦点关于直线l的对称点在圆 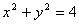 上,求此椭圆的方程。
上,求此椭圆的方程。
数学试题(理科)参考答案
一、CDACB DBDDB AC
二、13.3 14。—4 15。 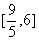 16。①②④
16。①②④
三、17.解:(1) 
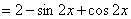
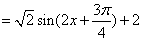 。
。 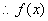 的最小正周期
的最小正周期 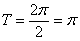 。
。
(2) 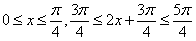
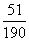
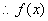 最大值是3,最小值是1。
最大值是3,最小值是1。
18. 解:(Ⅰ)记“厂家任取4件产品检验,其中至少有1件是合格品”为事件A
用对立事件A来算,有 
(Ⅱ) 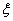 可能的取值为
可能的取值为 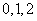
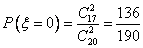 ,
,  ,
, 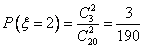
|
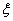
|
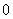
|

|

| |
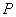
|
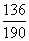
|
|

| | 
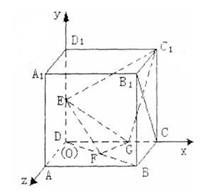 (解法二)如图建立空间直角坐标系
(解法二)如图建立空间直角坐标系