考生注重:考试时间120分钟,试卷总分150分。
一、填空题:(12×4’=48’)
1、集合  的一个非空真子集是__________
的一个非空真子集是__________
2、若 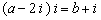 ,其中
,其中 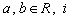 是虚数单位,则
是虚数单位,则 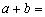 __________
__________
3、在等差数列 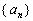 中,
中, 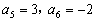 ,则
,则 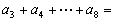 __________
__________
4、若 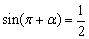 ,
, 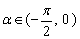 ,则
,则  __________
__________
5、设函数 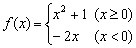 ,那么
,那么  _________
_________
6、已知圆的半径为2,圆心在 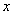 轴的正半轴上,且圆与直线3
轴的正半轴上,且圆与直线3 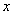 4
4 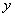 4 = 0相切,则圆的标准方程是_______________________
4 = 0相切,则圆的标准方程是_______________________
7、已知  是锐角
是锐角 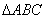 中
中  的对边,若
的对边,若 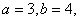
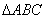 的面积为
的面积为 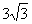 ,
,
则 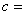
8、某机关的2008年新春联欢会原定10个节目已排成节目单,开演前又增加了两个反映军民联手抗击雪灾的节目,将这两个节目随机地排入原节目单,则这两个新节目恰好排在一起的概率是_______________
9、在极坐标系中,  是极点,设点
是极点,设点 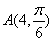 ,
,  ,则O点到AB所在直线的距离是
,则O点到AB所在直线的距离是
10、设定义在 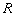 的函数
的函数 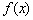 同时满足以下条件:①
同时满足以下条件:① 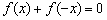 ;②
;② 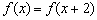 ;
;
③当 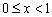 时,
时, 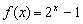 。则
。则 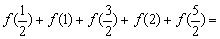 _____________
_____________
11、在平面直角坐标系中,横、纵坐标均为整数的点叫做格点.若函y=f(x)的图像恰好经过k 个格点,则称函数y=f(x)为k阶格点函数.已知函数:①y=2sinx;②y=cos(x  );③
);③  ;④
;④ 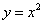 .其中为一阶格点函数的序号为 (注:把你认为正确论断的序号都填上)
.其中为一阶格点函数的序号为 (注:把你认为正确论断的序号都填上)
12、已知AB是椭圆 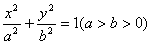 的长轴,若把该长轴
的长轴,若把该长轴  等分,过每个等分点作AB的垂线,依次交椭圆的上半部分于点
等分,过每个等分点作AB的垂线,依次交椭圆的上半部分于点  ,设左焦点为
,设左焦点为 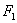 ,
,
则 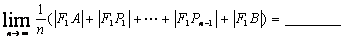
二、选择题(4×4’=16’)
13、假如a,b,c满足c<b<a且ac<0,那么下列选项中不一定成立的是 ---------- ( )
A. ab>ac B. c(b-a)>0 C. 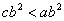 D. ac(a-c)<0
D. ac(a-c)<0
14、设a,b,c表示三条直线, 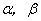 表示两个平面,下列命题中不正确的是---------( )
表示两个平面,下列命题中不正确的是---------( )
A. 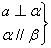
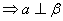 B.
B. 
C. 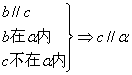 D.
D. 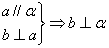
15、若 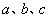 是常数,则“
是常数,则“  ”是
”是
“对任意  ,有
,有 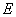 ”的 --------------------------- ( )
”的 --------------------------- ( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
16、由方程 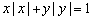 确定的函数
确定的函数 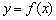 在
在 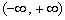 上是 --------- ( )
上是 --------- ( )
A.增函数 B.减函数 C.先增后减 D.先减后增
三、解答题:
17、(8 4)已知向量 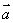 =(−cosx , sinx),
=(−cosx , sinx), 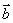 =(cosx ,
=(cosx , 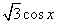 ),函数f(x)=
),函数f(x)= 
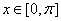
(1)求函数f(x)的最大值
(2)当函数f(x)取得最大值时,求向量 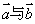 夹角的大小.
夹角的大小.
[解]
18、(6 6)在长方体 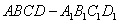 中(如图),
中(如图), 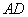 =
=  =1,
=1, 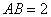 ,点E是AB上的动点
,点E是AB上的动点
(1)若直线  ,请你确定点
,请你确定点 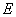 的位置,并求出此时异面直线
的位置,并求出此时异面直线 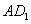 与
与 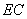 所成的角
所成的角
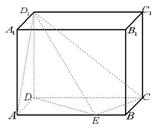 (2) 在(1)的条件下求二面角
(2) 在(1)的条件下求二面角 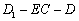 的大小
的大小
[解]
19、(7 7)已知等比数列 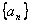 的首项
的首项 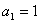 ,公比为
,公比为 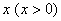 ,其前
,其前  项和为
项和为 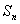
(1)求函数 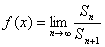 的解析式;(2)解不等式
的解析式;(2)解不等式 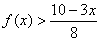 .
.
[解]
20、(4 6 4)电信局根据市场客户的不同需求,对某地区的手机套餐通话费提出两种优惠方案,则两种方案付电话费(元)与通话时间(分钟)之间的关系如图所示(实线部分)(MN平行CD)
(1)  若通话时间为两小时,按方案A,B各付话费多少元?
若通话时间为两小时,按方案A,B各付话费多少元?
(2) 方案B从500分钟以后,每分钟收费多少元?
(3) 通话时间在什么范围内,方案B比方案A优惠?
[解]


21、(4 6 6)设
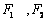
分别是椭圆C:
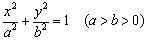
的左右焦点
(1)设椭圆C上的点 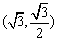 到
到 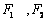 两点距离之和等于4,写出椭圆C的方程和焦点坐标
两点距离之和等于4,写出椭圆C的方程和焦点坐标
(2)设K是(1)中所得椭圆上的动点,求线段 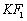 的中点B的轨迹方程
的中点B的轨迹方程
(3)设点P是椭圆C 上的任意一点,过原点的直线L与椭圆相交于M,N两点,当直线PM ,PN的斜率都存在,并记为  试探究
试探究 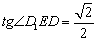 的值是否与点P及直线L有关,并证实你的结论。
的值是否与点P及直线L有关,并证实你的结论。
22、(4 7 7) 定义在  上的函数
上的函数  ,假如满足:对任意
,假如满足:对任意  ,存在常数
,存在常数 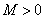 ,都有
,都有 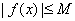 成立,则称
成立,则称 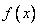 是
是  上的有界函数,其中
上的有界函数,其中 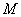 称为函数
称为函数 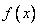 的上界.
的上界.
已知函数  ;
; 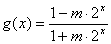 .
.
(1)当 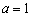 时,求函数
时,求函数 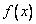 在
在 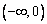 上的值域,并判定函数
上的值域,并判定函数 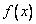 在
在 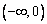 上是否为有界函数,请说明理由;
上是否为有界函数,请说明理由;
(2)若函数 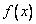 在
在 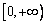 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数 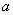 的取值范围;
的取值范围;
(3)若 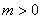 ,函数
,函数 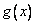 在
在 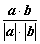 上的上界是
上的上界是  ,求
,求  的取值范围.
的取值范围.
[解]
参考答案
一、填空题:
1、 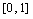 2、3 3、3 4、
2、3 3、3 4、  5、 3, -5 6、
5、 3, -5 6、 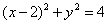
7、 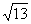 8、
8、 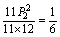 9、
9、  10、
10、 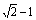 11、①③ 12、
11、①③ 12、 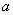
二、选择题(4×4’=16’)
13、C 14、D 15、A 16、 B
三、解答题:
17、[解] :(1)f(x)=  =−cos2x
=−cos2x 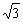 sinxcosx …………………2分
sinxcosx …………………2分
= 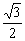 sin2x−
sin2x− 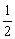 cos2x−
cos2x− 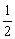 …………………………4分
…………………………4分
=sin(2x−  )−
)− 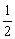 …………………………6分
…………………………6分
∵x∈[0,π],∴当x= 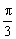 时,f(x)max=1−
时,f(x)max=1− 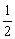 =
= 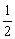 ………8分
………8分
(2)此时x= 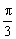 ,设向量
,设向量 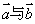 夹角为
夹角为  则cos
则cos  =
= 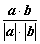 …………9分
…………9分
=  =
= 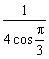 =
= 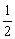 …………………………11分
…………………………11分
所以 向量 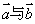 夹角为
夹角为 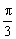 ………………12分
………………12分
18、  [解]:(1)
[解]:(1)
解法1:由 
 DE与CE垂直-----1分
DE与CE垂直-----1分
设AE=x,在直角三角形DEC中求得  -----2分
-----2分
所以点 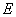 是AB的中点--------------3分
是AB的中点--------------3分
取CD的中点Q,则AQ平行与EC,所以 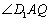 是所求的角------4分
是所求的角------4分
求解  得
得 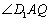 =
=  -------------5分
-------------5分
异面直线 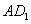 与EC所成的角为
与EC所成的角为  -------6分
-------6分
解法2:利用向量法
分别以DA,DC,D  所在的直线为X轴建立坐标系---------------------------------1分
所在的直线为X轴建立坐标系---------------------------------1分
设AE=x, 根据直线 
 -----2分
-----2分
所以点 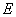 是AB的中点--------------3分
是AB的中点--------------3分
写出A(1,0,0) E(1,1,0 ) C (0,2,0)  (0,0,1)---------4分
(0,0,1)---------4分
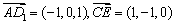
设 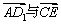 的夹角为
的夹角为 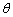 cos
cos 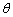 =
=  ----------------5分
----------------5分
异面直线 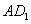 与
与 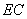 所成的角为
所成的角为  -----------6分
-----------6分
(2)解法1:由 
 DE与CE垂直,
DE与CE垂直,
所以 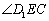 是所求
是所求 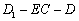 的平面角---8分
的平面角---8分
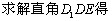
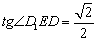 -------11分
-------11分
二面角 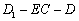 是
是  --------12分
--------12分
解法2:利用向量法求得二面角 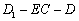 是
是 
19、[解]:(1)当 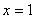 时,
时,  ,
, 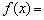
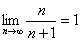 ;…………2分
;…………2分
当  且
且  时,
时,  ,
, 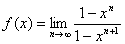 ,……………………4分
,……………………4分
若 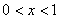 ,
, 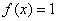 ;……………5分,若
;……………5分,若 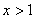 ,则
,则 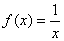 ,……………6分
,……………6分
综上, 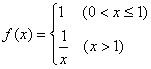 ……………………7分
……………………7分
(2)当 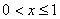 时,由
时,由 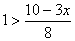 ,得
,得 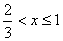 ;……………………10分
;……………………10分
当 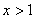 时,由
时,由 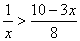 ,得
,得 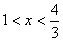 或
或 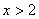 。………………13分
。………………13分
综上可得原不等式的解集为  。…………………14分
。…………………14分
20、[解]:设通话x分钟时,方案A,B的通话费分别为 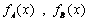 ---------1分
---------1分
(1)当x=120时  =116元
=116元  =168元-----------3分
=168元-----------3分
若通话时间为两小时,方案A付话费116元,方案B付话费168元------4分
(2) 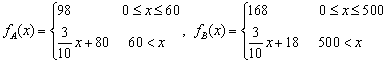 ----------7分
----------7分
当 
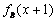 -
-  =0.3 --------------------------------9分
=0.3 --------------------------------9分
方案B从500分钟以后,每分钟收费0.3 元-------------------10分
(3) 当 
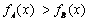 -------------------------------11分
-------------------------------11分
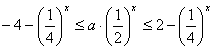
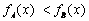 ----------------------12分
----------------------12分
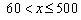 由
由 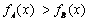 得
得  ----------13分
----------13分
综合:通话时间在 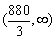 内方案B较优惠。----------14分
内方案B较优惠。----------14分
21、[解]:(1)由于点 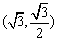 在椭圆上,
在椭圆上, 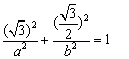 ------1分
------1分
2 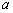 =4, ------2分
=4, ------2分
椭圆C的方程为 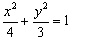 --------3分
--------3分
焦点坐标分别为(-1,0) ,(1,0)-----------4分
(2)设 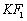 的中点为B(x, y)则点
的中点为B(x, y)则点 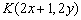 --------6分
--------6分
把K的坐标代入椭圆 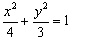 中得
中得 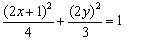 -----8分
-----8分
线段 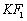 的中点B的轨迹方程为
的中点B的轨迹方程为 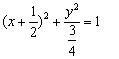 ----------10分
----------10分
(3)过原点的直线L与椭圆相交的两点M,N关于坐标原点对称
设 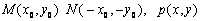 ----11分
----11分
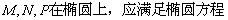 ,得
,得 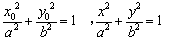 ------12分
------12分
 -------------------13分
-------------------13分
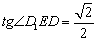 =
=  =
=  -----------15分
-----------15分
故: 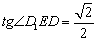 的值与点P的位置无关,同时与直线L无关,-----16分
的值与点P的位置无关,同时与直线L无关,-----16分
22、 [解]:(1)当 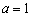 时,
时, 
因为  在
在 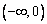 上递减,所以
上递减,所以 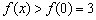 ,即
,即  在
在 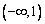 的值域为
的值域为 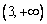
故不存在常数 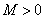 ,使
,使 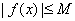 成立
成立
所以函数 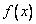 在
在 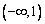 上不是有界函数。 ……………4分(没有判定过程,扣2分)
上不是有界函数。 ……………4分(没有判定过程,扣2分)
(2)由题意知, 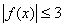 在
在 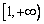 上恒成立。………5分
上恒成立。………5分
 ,
, 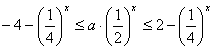
∴ 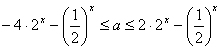 在
在 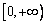 上恒成立………6分
上恒成立………6分
∴ 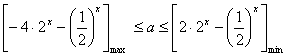 ………7分
………7分
设 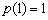 ,
,  ,
, 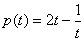 ,由
,由 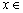
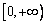 得 t≥1,
得 t≥1,
设  ,
, 
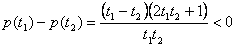
所以 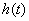 在
在 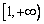 上递减,
上递减, 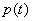 在
在 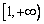 上递增,………9分(单调性不证,不扣分)
上递增,………9分(单调性不证,不扣分)
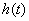 在
在 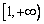 上的最大值为
上的最大值为 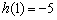 ,
, 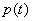 在
在 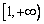 上的最小值为
上的最小值为 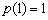
所以实数 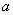 的取值范围为
的取值范围为  。…………………………………11分
。…………………………………11分
(3)  ,
,
∵ m>0 ,  ∴
∴ 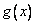 在
在 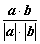 上递减,………12分
上递减,………12分
∴ 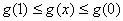 即
即 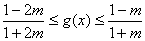 ………13分
………13分
①当 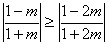 ,即
,即 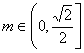 时,
时,  , ………14分
, ………14分
此时 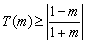 ,………16分
,………16分
②当 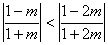 ,即
,即  时,
时, 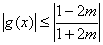 ,
,
此时 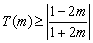 , ---------17分
, ---------17分
综上所述,当 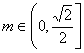 时,
时,  的取值范围是
的取值范围是 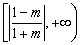 ;
;
当  时,
时,  的取值范围是
的取值范围是 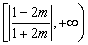 ………18
………18
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

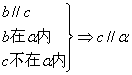
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
 (2) 在(1)的条件下求二面角
(2) 在(1)的条件下求二面角 ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
 若通话时间为两小时,按方案A,B各付话费多少元?
若通话时间为两小时,按方案A,B各付话费多少元?
 21、(4 6 6)设
21、(4 6 6)设 ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
 [解]:(1)
[解]:(1)![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
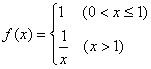
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
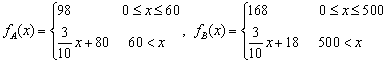
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
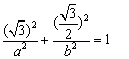
![]()
![]()
![]()
![]()
![]()
![]()
![]()
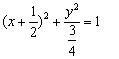
![]()
![]()
![]()

![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
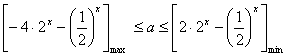
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
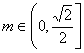
![]()
![]()
![]()

![]()
![]()
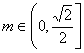
![]()
![]()

![]()
![]()
