|
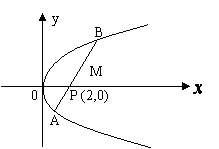 例1:已知直线 例1:已知直线  过点P(2,0),斜率为
过点P(2,0),斜率为 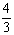 ,直线
,直线 
和抛物线 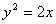 相交于A、B两点,
相交于A、B两点,
设线段AB的中点为M,求:
(1)P、M两点间的距离|PM|;
(2)M点的坐标;
(3)线段AB的长|AB|
解:(1)∵直线  过点P(2,0),斜率为
过点P(2,0),斜率为 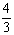 ,设直线的倾斜角为
,设直线的倾斜角为 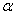 ,tg
,tg 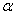 =
= 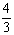
cos 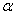 =
=  , sin
, sin 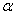 =
= 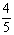 ∴直线
∴直线  的标准参数方程为
的标准参数方程为 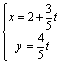 (t为参数)*
(t为参数)*
∵直线  和抛物线相交,将直线的参数方程代入抛物线方程
和抛物线相交,将直线的参数方程代入抛物线方程 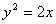 中,
中,
整理得 8t2-15t-50=0 Δ=152 4×8×50>0,设这个二次方程的两个根为t1、t2,由韦达定理得 t1+t2= 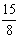 , t1t2=
, t1t2= 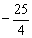 ,由M为线段AB的中点,根据t的几何意义,得| PM|=
,由M为线段AB的中点,根据t的几何意义,得| PM|= 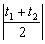 =
= 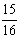
∵中点M所对应的参数为t M= 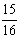 ,将此值代入直线的标准参数方程*,
,将此值代入直线的标准参数方程*,
M点的坐标为 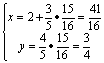 即 M(
即 M( 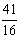 ,
, 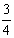 )
)
(1) |AB|=∣t 2-t 1∣= 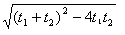 =
= 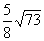
点拨:利用直线  的标准参数方程中参数t的几何意义,在解决诸如直线
的标准参数方程中参数t的几何意义,在解决诸如直线  上两点间的距离、直线
上两点间的距离、直线  上某两点的中点以及与此相关的一些问题时,比用直线
上某两点的中点以及与此相关的一些问题时,比用直线  的普通方程来解决显得比较灵活和简捷.
的普通方程来解决显得比较灵活和简捷.
例2:已知直线  经过点P(1,-3
经过点P(1,-3  ),倾斜角为
),倾斜角为 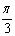 ,
,
(1)求直线  与直线
与直线  :
: 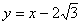 的交点Q与P点的距离| PQ|;
的交点Q与P点的距离| PQ|;
(2)求直线  和圆
和圆 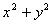 =16的两个交点A,B与P点的距离之积.
=16的两个交点A,B与P点的距离之积.
解:(1)∵直线  经过点P(1,-3
经过点P(1,-3  ),倾斜角为
),倾斜角为 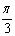 ,∴直线
,∴直线  的标准参数方
的标准参数方
程为 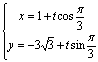 ,即
,即  (t为参数)代入直线
(t为参数)代入直线  :
:
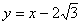 得
得  整理,解得t=4 2
整理,解得t=4 2 
t=4 2  即为直线
即为直线  与直线
与直线  的交点Q所对应的参数值,根据参数t的几
的交点Q所对应的参数值,根据参数t的几
何意义可知:|t|=| PQ|,∴| PQ|=4 2  .
.
(2) 把直线  的标准参数方程为
的标准参数方程为  (t为参数)代入圆的方程
(t为参数)代入圆的方程
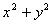 =16,得
=16,得 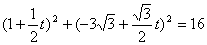 ,整理得:t2-8t 12=0,
,整理得:t2-8t 12=0,
Δ=82-4×12>0,设此二次方程的两个根为t1、t2 则t1t2=12
根据参数t的几何意义,t1、t2 分别为直线和圆 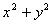 =16的两个交点
=16的两个交点
A, B所对应的参数值,则|t1|=| PA|,|t2|=| PB|,
所以| PA|·| PB|=|t1 t2|=12
点拨:利用直线标准参数方程中的参数t的几何意义解决距离问题、距离的乘积(或商)的问题,比使用直线的普通方程,与另一曲线方程联立先求得交点坐标再利用两点间的距离公式简便.
例3:设抛物线过两点A(-1,6)和B(-1,-2),对称轴与  轴平行,开口向右,
轴平行,开口向右,
直线y=2  7被抛物线截得的线段长是4
7被抛物线截得的线段长是4 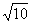 ,求抛物线方程.
,求抛物线方程.
解:由题意,得抛物线的对称轴方程为y=2.设抛物线顶点坐标为( 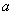 ,2)
,2)
方程为(y―2)2=2P(x- 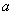 ) (P>0) ①
) (P>0) ①
∵点B(-1,-2)在抛物线上,∴(―2―2)2=2P(-1- 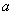 )
)
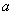 P=-8-P 代入① 得(y―2)2=2P
P=-8-P 代入① 得(y―2)2=2P  +2P 16 ②
+2P 16 ②
将直线方程y=2  7化为标准的参数方程tg
7化为标准的参数方程tg 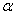 =2,
=2, 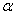 为锐角,
为锐角,
cos 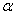 =
= 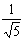 , sin
, sin 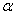 =
= 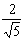 得
得 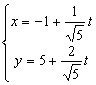 (t为参数) ③
(t为参数) ③
∵直线与抛物线相交于A,B, ∴将③代入②并化简得:
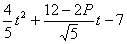 =0 ,由Δ=
=0 ,由Δ= 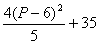 >0,可设方程的两根为t1、t2,
>0,可设方程的两根为t1、t2,
又∵|AB|=∣t 2-t 1∣= 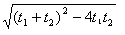 =4
=4 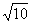
 =(4
=(4 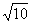 )2 化简,得(6-P)2=100
)2 化简,得(6-P)2=100
∴ P=16 或P=-4(舍去) 所求的抛物线方程为(y―2)2=32  +48
+48
点拨:(1)(对称性) 由两点A(-1,6)和B(-1,-2)的对称性及抛物线的对称性质,设出抛物线的方程(含P一个未知量,由弦长AB的值求得P).
(2)利用直线标准参数方程解决弦长问题.此题也可以运用直线的普通方程与抛物线方程联立后,求弦长。对于有些题使用直线的参数方程相对简便些.
例4:已知椭圆 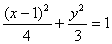 ,AB是通过左焦点F1的弦,F2为右焦点,
,AB是通过左焦点F1的弦,F2为右焦点,
求| F2A|·| F2B|的最大值.
解:由椭圆方程知 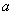 =2,b=
=2,b=  ,c=1, F1(0,0),F2(2,0),设过的弦所在直线的
,c=1, F1(0,0),F2(2,0),设过的弦所在直线的
参数方程为 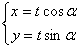 (t为参数) 代入椭圆方程整理得
(t为参数) 代入椭圆方程整理得
(3+sin2 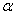 )t2-6 t cos
)t2-6 t cos 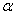 -9=0 ,Δ=36cos2
-9=0 ,Δ=36cos2 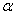 +36(3+sin2
+36(3+sin2 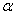 )>0
)>0
此方程的解为t1、t2,分别为A、B两点
对应的参数,由韦达定理t1+t2= 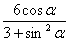 t1 t2=
t1 t2= 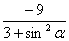
根据参数t的几何意义,t1、t2 分别为过点F1的直线和椭圆的两个交点
A, B所对应的参数值,| F1A|=|t1| |F1B|=|t2|
|AB|=∣t 2-t 1∣= 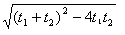 =
= 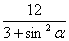
| F1A|·|F1B|=|t1|·|t2|=|t1t2|
由椭圆的第一定义| F1A|+| F2A|=2 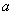 =4, | F1B| | F2B|=2
=4, | F1B| | F2B|=2 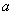 =4
=4
| F2A|·| F2B|=(4-| F1A|)(4-| F1B|)=16-4|AB| | F1A|·|F1B|
=16-4∣t 2-t 1∣ |t1t2|=16-4 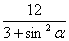
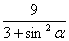 =16-
=16- 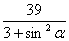
当sin2 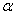 =1时,| F2A|·| F2B|有最大值
=1时,| F2A|·| F2B|有最大值 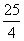
点拨:求过定点的直线与圆锥曲线相交的距离之积,利用直线的参数方程解
题,此题中两定点F1(0,0),F2(2,0),显然F1坐标简单,因此选择过F1
的直线的参数方程,利用椭圆的定义将| F2A|·| F2B| 转化为| F1A|·|F1B|.
方法总结:利用直线  的参数方程
的参数方程  (t为参数),给研究直线与圆锥曲线C:F(
(t为参数),给研究直线与圆锥曲线C:F( 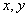 )=0的位置关系提供了简便的方法.
)=0的位置关系提供了简便的方法.
一般地,把  的参数方程代入圆锥曲线C:F(
的参数方程代入圆锥曲线C:F( 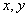 )=0后,可得一个关于t 的一元二次方程,
)=0后,可得一个关于t 的一元二次方程, 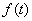 =0,
=0,
1、(1)当Δ<0时,  与C相离;(2) 当Δ=0时,
与C相离;(2) 当Δ=0时,  与C相切;(3) 当Δ>0时,
与C相切;(3) 当Δ>0时,
 与C相交有两个交点;
与C相交有两个交点;
2、当Δ>0时,方程 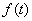 =0的两个根分别记为t1、t2,把t1、t2分别代入
=0的两个根分别记为t1、t2,把t1、t2分别代入  的参数方程即可求的
的参数方程即可求的  与C的两个交点A和B的坐标.
与C的两个交点A和B的坐标.
3、定点M0( 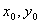 )是弦AB中点
)是弦AB中点 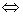 t1 t2=0
t1 t2=0
4、  被C截得的弦AB的长|AB|=|t1-t2|;M0A·M0B= t1·t2;弦AB中点M点对应的参数为
被C截得的弦AB的长|AB|=|t1-t2|;M0A·M0B= t1·t2;弦AB中点M点对应的参数为 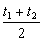 ;| M0M |=
;| M0M |= 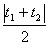
|