| |
|
[组图]高考数学复习调研试卷
|
| 查询数高考考试的详细结果
|
|
高考数学复习调研试卷
一、填空题(每小题5分,共70分)
1.p:“ 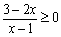 ”和q:“
”和q:“ 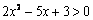 ”,则
”,则 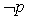 是q的 条件.
是q的 条件.
2.设直线 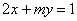 的倾斜角为
的倾斜角为  ,若
,若 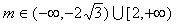 ,则角
,则角  的取值范围是___
的取值范围是___
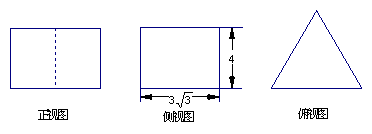 3.若一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如下图所示,则这个棱柱的体积为 . 3.若一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如下图所示,则这个棱柱的体积为 .
4.我国于07年10月24日成功发射嫦娥一号卫星,并经四次变轨飞向月球。嫦娥一号绕地球运行的轨迹是以地球的地心为焦点的椭圆。若第一次变轨前卫星的近地点到地心的距离为m,远地点到地心的距离为n,第二次变轨后两距离分别为2m、2n(近地点是指卫星到地面的最近距离,远地点是最远距离),则第一次变轨前的椭圆的离心率比第二次变轨后的椭圆的离心率 .(填变大或变小或不变) 不变
5.设O是△ABC内部一点,且 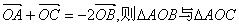 的面积之比为 .
的面积之比为 .
6.若函数  是定义在(0,
是定义在(0, 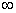 )上的增函数,且对一切x>0,y>0满足
)上的增函数,且对一切x>0,y>0满足 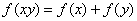 ,则不等式
,则不等式 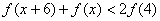 的解集为 .
的解集为 .
7.设变量 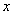 ,
, 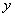 满足约束条件
满足约束条件 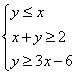 ,则目标函数
,则目标函数 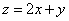 的最小值为
的最小值为
8.一个正方体的顶点都在球面上,它的棱长是4cm,则这个球的体积等于 cm3
9.若函数 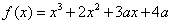 有一个极大值和一个极小值,则
有一个极大值和一个极小值,则 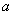 的取值范围是 .
的取值范围是 .
10.已知函数 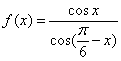 ,则
,则 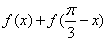 的值为 .
的值为 .
11. 某公司一年需购买某种货物 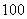 吨,每次都购买
吨,每次都购买 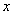 吨,运费为
吨,运费为 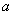 万元/次,一年的总存储费用为
万元/次,一年的总存储费用为 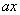 万元,要使一年的总运费与总存储费用之和最小,则
万元,要使一年的总运费与总存储费用之和最小,则  吨.
吨.
12.若  等于
等于
13.已知 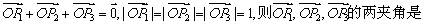
14.对正整数n,设抛物线 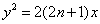 ,过点P(2n,0)任作直线
,过点P(2n,0)任作直线 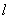 交抛物线于
交抛物线于 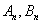 两点,则数列
两点,则数列 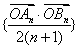 的前n 项和为_ _
的前n 项和为_ _
二、解答题(本大题共6小题,共90分)
15.(本题满分14分)
在 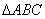 中,
中, 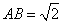 ,
, 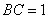 ,
, 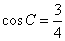 .
.
(1)求  的值;(2)求
的值;(2)求  的值.
的值.
16.(本题满分14分)
经统计,某大型商场一个结算窗口天天排队结算的人数及相应的概率如下: |
排队人数 |
0—5 |
6—10 |
11—15 |
16—20 |
21—25 |
25人以上 |
|
概 率 |
0.1 |
0.15 |
0.25 |
0.25 |
0.2 |
0.05 |
|
(I)天天不超过20人排队结算的概率是多少?
(Ⅱ)一周7天中,若有3天以上(含3天)出现超过15人排队结算的概率大于0.75,商场就需要增加结算窗口,请问该商场是否需要增加结算窗口?
17.(本题满分15分)
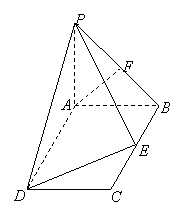
如图: 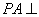 平面
平面 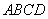 ,四边形
,四边形 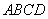 是矩形,
是矩形, 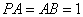 ,
, 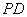 与平面
与平面 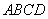 所成的角是
所成的角是 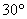 ,点
,点 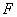 是
是 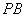 的中点,点
的中点,点 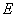 在边
在边 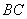 上移动.
上移动.
 (1)当点 (1)当点 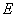 为
为 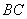 的中点时,试判定
的中点时,试判定 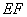 与平面
与平面 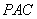 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)证实:不论点 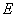 在边
在边 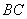 上何处,都有
上何处,都有 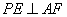 ;
;
18.(本题满分15分)
某单位决定投资3200元建一长方体状仓库,高度恒定,它的后墙利用旧墙不花钱,正面用铁珊,每米造价40元,两侧墙砌砖,每米造价45元,顶部每平方米造价20元,计算:
(1)仓库面积S的最大答应值是多少?
(2)为了使仓库面积S达到最大,而实际投资又不超过预算,那么正面用铁珊应设计为多长?
19.(本题共16分)
已知AB是椭圆  的一条弦,向量
的一条弦,向量 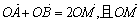 =(2,1)以M为左焦点,以椭圆的右准线为相应准线的双曲线左支与直线AB交于点N(4,-1)
=(2,1)以M为左焦点,以椭圆的右准线为相应准线的双曲线左支与直线AB交于点N(4,-1)
①求椭圆的离心率e1;
②设双曲线的离心率为e2,e1 e2= 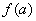 ,求
,求 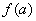 的解析式,并求它的定义域和值域。
的解析式,并求它的定义域和值域。
20.(本题满分16分)
已知二次函数  的二次项系数为
的二次项系数为 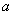 ,且不等式
,且不等式  的解集为
的解集为 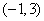 .
.
(1)若方程 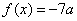 有两个相等的实数根,求
有两个相等的实数根,求  的解析式;
的解析式;
(2)若函数 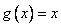
 在区间
在区间 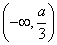 内单调递减,求
内单调递减,求 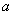 的取值范围;
的取值范围;
(3)当  时,证实方程
时,证实方程  仅有一个实数根.
仅有一个实数根.
答案
一、1.必要不充分 2.  3.
3. 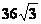 4.不变 5.
4.不变 5.  6.
6. 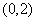 7. 3
7. 3
8. 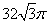 9.
9. 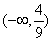 10.
10. 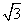 11. 10 12. 2006
11. 10 12. 2006
13 120° 14. 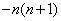
15.解:(1)在 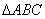 中,由
中,由 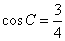 ,得
,得 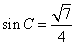 , 又由正弦定理:
, 又由正弦定理: 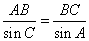 得:
得: 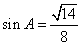 . ……………………6分
. ……………………6分
(2)由余弦定理: 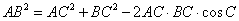 得:
得:  ,
,
即 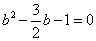 ,解得
,解得  或
或 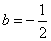 (舍去),所以
(舍去),所以 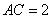 . ……10分
. ……10分
所以, 

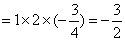
即 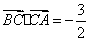 . …………………14分
. …………………14分
16. (I)天天不超过20人排队结算的概率为:P=0.1 0.15 0.25 0.25=0.75,即不超过20
人排队结算的概率是0.75. ……………………4分
(Ⅱ)天天超过15人排队结算的概率为:0.25 0.2 0.05=  ,……………6分
,……………6分
一周7天中,没有出现超过15人排队结算的概率为 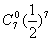 ;
;
一周7天中,有一天出现超过15人排队结算的概率为  ;
;
一周7天中,有二天出现超过15人排队结算的概率为 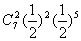 ;……………10分
;……………10分
所以有3天或3天以上出现超过15人排队结算的概率为:
 ,
,
所以,该商场需要增加结算窗口. ……………………14
17.(1)当点 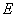 为
为 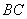 的中点时,
的中点时, 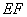 与平面
与平面 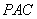 平行.
平行.
∵在 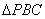 中,
中, 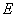 、
、 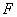 分别为
分别为 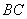 、
、 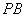 的中点
的中点
∴ 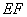 ∥
∥ 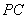 又
又  平面
平面 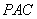 ,而
,而 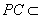 平面
平面 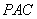
∴ 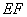 ∥平面
∥平面 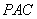 . ………7分
. ………7分
(2)证实(略证):易证 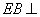 平面
平面 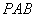 ,又
,又 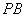 是
是 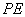 在平面
在平面 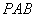 内的射影,
内的射影,
 ,∴
,∴ 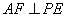 . ……………………8分
. ……………………8分
18. S最大值是100 m2,铁栅长是15m.
19.解:①由 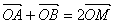 ,则M为AB的中点(2,1).
,则M为AB的中点(2,1).
设 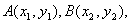 则
则 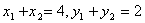 ,
,
且A、B在椭圆上 ∴ 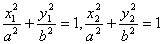
两式相减得 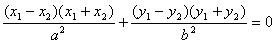
∴ 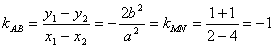
∴a2=2b2 又a2=b2 c2 ∴b2=c2
∴椭圆率心离 
②由题设可知,点N在椭圆右准线L: 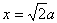 的左侧,所以
的左侧,所以 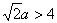
所以 
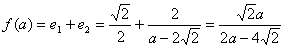
由题意设 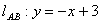 代入椭圆方程,消去y得
代入椭圆方程,消去y得 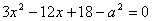
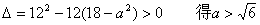
由 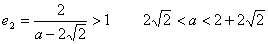
∴ 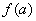 的定义域为
的定义域为 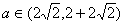
又 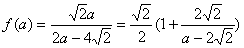 故值域
故值域 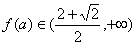
20.解:(1) 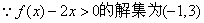 ,
,
∴可设 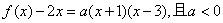 ,
,
因而 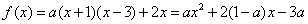 ①
①
由 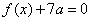 得
得  ②
②
∵方程②有两个相等的根,
∴ 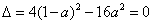 ,即
,即 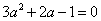 解得
解得  或
或 
由于 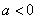 ,
,  (舍去),将
(舍去),将  代入 ① 得
代入 ① 得  的解析式
的解析式 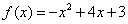 . …………………6分
. …………………6分
(2) 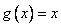
 =
= 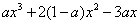 ,
,
∵  在区间
在区间 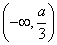 内单调递减,
内单调递减,
∴  在
在 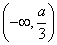 上的函数值非正,
上的函数值非正,
由于 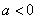 ,对称轴
,对称轴  ,故只需
,故只需 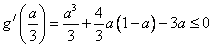 ,注重到
,注重到 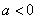 ,∴
,∴ 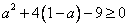 ,得
,得 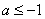 或
或 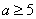 (舍去)
(舍去)
故所求a的取值范围是 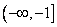 . …………………11分
. …………………11分
(3)  时,方程
时,方程  仅有一个实数根,即证方程
仅有一个实数根,即证方程  仅有一个实数根.令
仅有一个实数根.令 
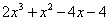 ,由
,由 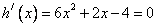 ,得
,得 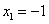 ,
,  ,易知
,易知 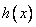 在
在 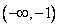 ,
, 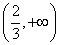 上递增,在
上递增,在 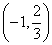 上递减,
上递减, 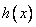 的极大值
的极大值 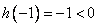 ,
, 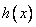 的极小值
的极小值 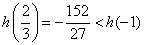 ,故函数
,故函数 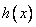 的图像与
的图像与 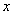 轴仅有一个交点,∴
轴仅有一个交点,∴  时,方程
时,方程  仅有一个实数根,得证. ……………………16分
仅有一个实数根,得证. ……………………16分
|
 (1)当点
(1)当点