|
一、选择题:本大题共8小题,每小题5分,共40分。
1、复数 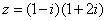 的实部是( B )
的实部是( B )
A、 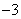 B、
B、 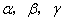 C、
C、 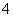 D、
D、 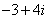
2、函数 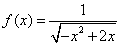 的定义域为( C )
的定义域为( C )
A、 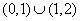 B、
B、 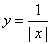 C、
C、 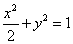 D、
D、 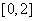
3、原命题:“设 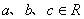 ,若
,若 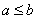 则
则 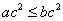 ”的逆命题、否命题、逆否命题中真命题共有( B )
”的逆命题、否命题、逆否命题中真命题共有( B )
A、0个 B、1个 C、2个 D、3个
4、设向量  ,则
,则 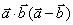 等于( C )
等于( C )
A、 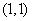 B、
B、 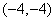 C、
C、 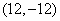 D、
D、 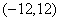
4.若 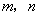 是两条不同的直线,
是两条不同的直线, 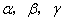 是三个不同的平面,则下列命题中的真命题是( )
是三个不同的平面,则下列命题中的真命题是( )
A.若 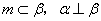 ,则
,则 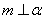 B.若
B.若 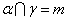
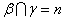 ,
, 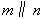 ,则
,则 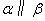
C.若 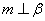 ,
,  ,则
,则 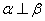 D.若
D.若 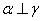 ,
, 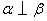 ,则
,则 
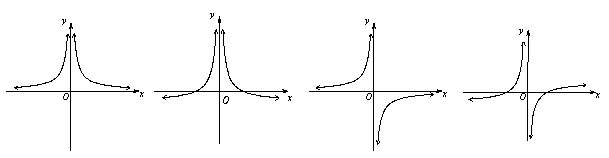 6、函数 6、函数 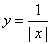 的图象大致是( A )
的图象大致是( A )
A、 B、 C、 D、
7、已知椭圆的中心为原点,离心率 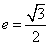 ,且它的一个焦点与抛物线
,且它的一个焦点与抛物线 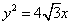 的焦点重合,则此椭圆方程为( A )
的焦点重合,则此椭圆方程为( A )
A、 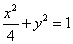 B、
B、 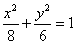
C、 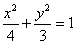 D、
D、 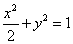
8、对任意实数 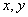 ,定义运算
,定义运算  ,其中
,其中 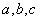 是常数,等式右边的运算是通常的加法和乘法运算。已知
是常数,等式右边的运算是通常的加法和乘法运算。已知 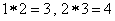 ,并且有一个非零常数
,并且有一个非零常数 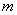 ,使得对任意实数
,使得对任意实数 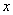 ,都有
,都有 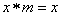 ,则
,则 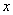 的值是( C )
的值是( C )
A、 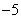 B、
B、 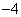 C、
C、 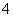 D、
D、 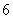
二、填空题:本大题共7小题,每小题5分,满分30分.其中13~15是选做题,考生只能选做二题,三题全答的,只计算前两题得分.
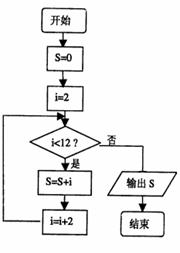
9、如右下图给出一个程序框图,其运行结果是 。
 10.若 10.若 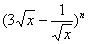 的展开式各项系数和为64,则展开式中的常数项为 。
的展开式各项系数和为64,则展开式中的常数项为 。
11.一个几何体的三视图及其尺寸如下(单位:㎝),
则该几何体的表面积是 ,体积是 .
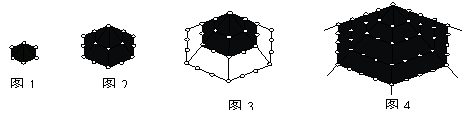
12.在一次珠宝展览会上,某商家展出一套珠宝首饰,第一件首饰是1颗珠宝, 第二件首饰是由6颗珠宝构成如图1所示的正六边形, 第三件首饰是由15颗珠宝构成如图2所示的正六边形, 第四件首饰是由28颗珠宝构成如图3所示的正六边形, 第五件首饰是由45颗珠宝构成如图4所示的正六边形, 以后每件首饰都在前一件上,按照这种规律增加一定数量的珠宝,使它构成更大的正六边形,依此推断,设第n件首饰为 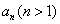 ,则
,则 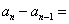 _
_ 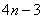 _____________ (结果用
_____________ (结果用 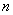 表示)
表示)
13.(坐标系与参数方程选做题)以极坐标系中的点 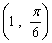 为圆心,1为半径的圆的方程是 ;
为圆心,1为半径的圆的方程是 ;
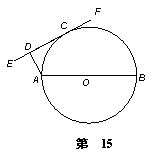 14.(不等式选讲选做题)不等式 14.(不等式选讲选做题)不等式 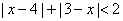 的解集是 ;
的解集是 ;
15.(几何证实选讲选做题)
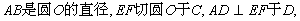
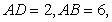 则
则 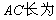 _______.
_______.
答题卷
一、选择题:(共8小题,每小题5分,共计40分)
二、填空题:(共6小题,每小题5分,共计30分)
9. 10.
11. 12.
13. 14. 15.
三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证实过程和演算步骤.
16.(满分12分)在△ABC中,角A、B、C所对边分别为a,b,c,已知 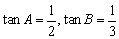 ,且最长边的边长为l.求: (I)角C的大小; (II)△ABC最短边的长.
,且最长边的边长为l.求: (I)角C的大小; (II)△ABC最短边的长.
17.(本小题满分12分)一个口袋中装有大小相同的2个白球和4个黑球.(Ⅰ)采取放回抽样方式,从中摸出两个球,求:(1)两球恰好颜色不同的概率;(Ⅱ)采取不放回抽样方式,从中摸出两个球,求摸得白球的个数的期望和方差.(方差: 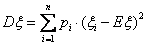 )
)
18.(本小题满分14分)
如图,三棱柱ABC—A1B1C1中,AA1⊥面ABC,BC⊥AC,BC=AC=2,AA1=3,D为AC的中点.
(Ⅰ)求证:AB1//面BDC1;
(Ⅱ)求二面角C1—BD—C的余弦值;
(Ⅲ)在侧棱AA1上是否存在点P,
使得CP⊥面BDC1?并证实你的结论.
19.(本题满分14分)已知函数 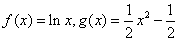 .
.
(1)求 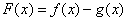 在
在 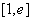 上的最大值,最小值(
上的最大值,最小值( 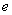 是自然对数的底);
是自然对数的底);
(2)当 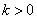 时,试讨论方程
时,试讨论方程  的解的个数.
的解的个数.
20.(本小题满分14分)已知动圆过定点 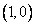 ,且与直线
,且与直线 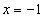 相切.
相切.
(1) 求动圆的圆心轨迹 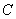 的方程;
的方程;
(2) 是否存在直线 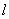 ,使
,使 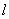 过点(0,1),并与轨迹
过点(0,1),并与轨迹 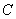 交于
交于 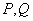 两点,且满足
两点,且满足  ?若存在,求出直线
?若存在,求出直线 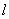 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
21.(本题满分14分)
已知数列 {an}、{bn} 满足:a1 = EQ \F(1,4) ,an bn = 1,bn 1 = EQ \F(bn,1-an2)
(1) 求证 bn 1 = EQ \F(1,2-bn) ;并求b1, b2, b3, b4的值;
(2) 求数列 {bn} 的通项公式;
(3) 设 Sn = a1a2 a2a3 a3a4 … anan 1,求实数a为何值时 4aSn < bn 恒成立.
答案
三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证实过程和演算步骤.
16.(满分12分)在△ABC中,角A、B、C所对边分别为a,b,c,已知 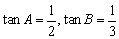 ,且最长边的边长为l.求: (I)角C的大小; (II)△ABC最短边的长.
,且最长边的边长为l.求: (I)角C的大小; (II)△ABC最短边的长.
解:(I)tanC=tan[π-(A+B)]=-tan(A+B) 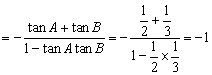
∵ 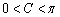 , ∴
, ∴ 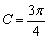 ……………………5分
……………………5分
(II)∵0<tanB<tanA,∴A、B均为锐角, 则B<A,又C为钝角,
∴最短边为b ,最长边长为c……………………7分
由 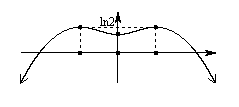 ,解得
,解得 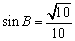 ……………………9分
……………………9分
由 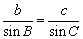 ,∴
,∴ 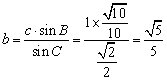 ………………12分
………………12分
17.(本小题满分12分)一个口袋中装有大小相同的2个白球和4个黑球.(Ⅰ)采取放回抽样方式,从中摸出两个球,求:(1)两球恰好颜色不同的概率;(Ⅱ)采取不放回抽样方式,从中摸出两个球,求摸得白球的个数的期望和方差.(方差: 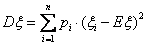 )
)
解:
(Ⅰ)解法一:“有放回摸两次,颜色不同”指“先白再黑”或“先黑再白”,
记“有放回摸球两次,两球恰好颜色不同”为事件  ,…………2分
,…………2分
∵“两球恰好颜色不同”共 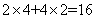 种可能,………5分
种可能,………5分
∴ 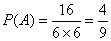 .…………7分
.…………7分
解法二:“有放回摸取”可看作独立重复实验, …………2分
∵每次摸出一球得白球的概率为 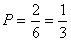 .…………5分
.…………5分
∴“有放回摸两次,颜色不同”的概率为 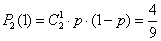 . ………7分
. ………7分
(Ⅱ)设摸得白球的个数为 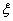 ,依题意得:
,依题意得:
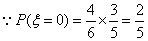 ,
, 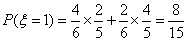 ,
, 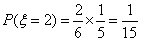 .…………10分
.…………10分
∴ 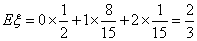 ,……12分
,……12分
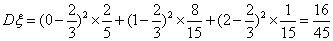 .…………14分
.…………14分
18.(本小题满分14分)
如图,三棱柱ABC—A1B1C1中,AA1⊥面ABC,BC⊥AC,BC=AC=2,AA1=3,D为AC的中点.
(Ⅰ)求证:AB1//面BDC1;
(Ⅱ)求二面角C1—BD—C的余弦值;
(Ⅲ)在侧棱AA1上是否存在点P,
使得CP⊥面BDC1?并证实你的结论.
(I)证实:
连接B1C,与BC1相交于O,连接OD
∵BCC1B1是矩形,
∴O是B1C的中点.
又D是AC的中点,
∴OD//AB1.………………………………………………2分
∵AB1 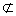 面BDC1,OD
面BDC1,OD 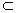 面BDC1,
面BDC1,
∴AB1//面BDC1.…………………………………………4分
(II)解:如力,建立空间直角坐标系,则
C1(0,0,0),B(0,3,2),C(0,3,0),A(2,3,0),
D(1,3,0)……………………5分
设 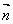 =(x1,y1,z1)是面BDC1的一个法向量,则
=(x1,y1,z1)是面BDC1的一个法向量,则
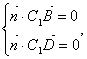
即 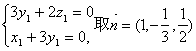 .…………6分
.…………6分
易知 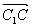 =(0,3,0)是面ABC的一个法向量.
=(0,3,0)是面ABC的一个法向量.
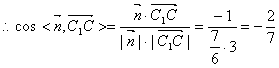 .…………………………8分
.…………………………8分
∴二面角C1—BD—C的余弦值为 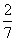 .………………………………9分
.………………………………9分
(III)假设侧棱AA1上存在一点P(2,y,0)(0≤y≤3),使得CP⊥面BDC1.
则 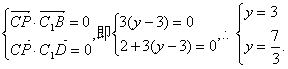
∴方程组无解.
∴假设不成立.……………………………………………………11分
∴侧棱AA1上不存在点P,使CP⊥面BDC1.…………………12分
19.(本题满分14分)
已知函数 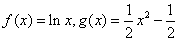 .
.
(1)求 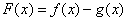 在
在 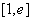 上的最大值,最小值(
上的最大值,最小值( 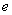 是自然对数的底);
是自然对数的底);
(2)当 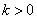 时,试讨论方程
时,试讨论方程  的解的个数.
的解的个数.
解:(1) 
因为 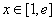 ,所以
,所以 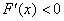 ,
,
所以 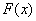 在
在 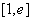 上单调递减,
上单调递减,
所以当 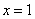 时,
时, 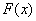 取得最大值
取得最大值  ;当
;当 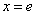 时,
时, 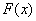 取得最小值
取得最小值 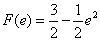 .
.
(2) 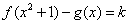 即
即
 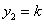 .
.
|
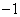 O 1 x
O 1 x
| | 设 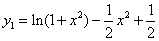 ,
, 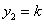 ,
,
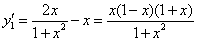 ,令
,令 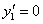 得
得 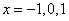 .
.
由图象得:①当 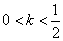 时,原方程有2个解;
时,原方程有2个解;
②当 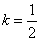 时,原方程有3个解;
时,原方程有3个解;
③当 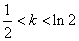 时,原方程有4个解;
时,原方程有4个解;
④当 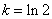 时,原方程有2个解;
时,原方程有2个解;
⑤当 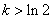 时,原方程无解.
时,原方程无解.
20.(本小题满分14分)
已知动圆过定点 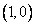 ,且与直线
,且与直线 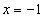 相切.
相切.
(1) 求动圆的圆心轨迹 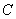 的方程;
的方程;
(2) 是否存在直线 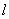 ,使
,使 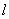 过点(0,1),并与轨迹
过点(0,1),并与轨迹 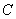 交于
交于 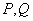 两点,且满足
两点,且满足  ?若存在,求出直线
?若存在,求出直线 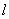 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
19.(本小题满分14分)
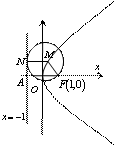 解:(1)如图,设 解:(1)如图,设 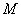 为动圆圆心,
为动圆圆心, 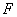
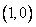 ,过点
,过点 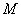 作直线
作直线 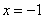
的垂线,垂足为 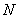 ,由题意知:
,由题意知: 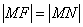 …………………2分
…………………2分
即动点 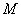 到定点
到定点 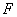 与到定直线
与到定直线 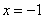 的距离相等,
的距离相等,
由抛物线的定义知,点 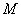 的轨迹为抛物线,其中
的轨迹为抛物线,其中 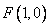 为焦点,
为焦点,
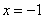 为准线, ……………………………………3分
为准线, ……………………………………3分
∴动圆圆心的轨迹方程为 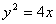 ……………………………………5分
……………………………………5分
(2)解法一:由题可设直线 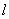 的方程为
的方程为 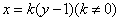
由  得
得 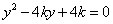 △
△ 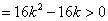 ,
, 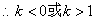 …………7分
…………7分
设 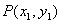 ,
, 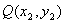 ,则
,则 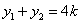 ,
, 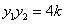 ……………………………………………9分
……………………………………………9分
由  ,即
,即  ,
, 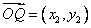 ,于是
,于是 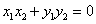 , ……11分
, ……11分
即 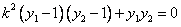 ,
,  ,
,
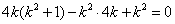 ,解得
,解得 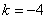 或
或 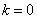 (舍去) …………………………………13分
(舍去) …………………………………13分
又 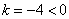 , ∴ 直线
, ∴ 直线 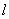 存在,其方程为
存在,其方程为 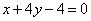 ……………………………14分
……………………………14分
解法二:显然直线的斜率存在,由题可设直线 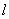 的方程为
的方程为 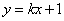
由 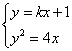 得
得 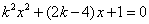
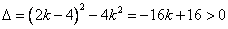
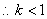 ……………………………………7分
……………………………………7分
设 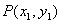 ,
, 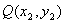 ,则
,则 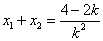 ,
, 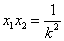 …………………………………9分
…………………………………9分
由  ,即
,即  ,
, 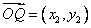 ,于是
,于是 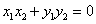 , ……11分
, ……11分
即 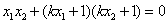 ,
, 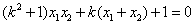 ,
,
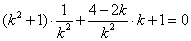 ,解得
,解得 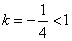 ……………………………13分
……………………………13分
∴ 直线 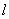 存在,其方程为
存在,其方程为 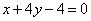 ……………………………14分
……………………………14分
21.(本题满分14分)
已知数列 {an}、{bn} 满足:a1 = EQ \F(1,4) ,an bn = 1,bn 1 = EQ \F(bn,1-an2)
(1) 求证 bn 1 = EQ \F(1,2-bn) ;并求b1, b2, b3, b4的值;
(2) 求数列 {bn} 的通项公式;
(3) 设 Sn = a1a2 a2a3 a3a4 … anan 1,求实数a为何值时 4aSn < bn 恒成立.
20. 解:(1) bn 1 = EQ \F(bn,(1-an) (1 an)) = EQ \F(bn,bn (2-bn)) = EQ \F(1,2-bn)
∵ a1 = EQ \F(1,4) ,b1 = EQ \F(3,4) ∴ b2 = EQ \F(4,5) ,b3 = EQ \F(5,6) ,b4 = EQ \F(6,7) (4分)
(2) ∵ bn 1-1 = EQ \F(1,2-bn) -1 ∴ EQ \F(1,bn 1-1) = EQ \F(2-bn,bn-1) = -1 EQ \F(1,bn-1)
∴ 数列{ EQ \F(1,bn-1) }是以-4为首项,-1为公差的等差数列
∴ EQ \F(1,bn-1) = -4-(n-1) = -n-3
∴ bn = 1- EQ \F(1,n 3) = EQ \F(n 2,n 3) (8分)
(3) an = 1-bn = EQ \F(1,n 3)
∴ Sn = a1a2 a2a3 … anan 1 = EQ \F(1,4×5) EQ \F(1,5×6) … EQ \F(1,(n 3)(n 4)) = EQ \F(1,4) - EQ \F(1,n 4)
= EQ \F(n,4 (n 4))
∴ 4aSn-bn = EQ \F(an,n 4) - EQ \F(n 2,n 3) = EQ \F((a-1) n 2 (3a-6) n-8,(n 3) (n 4))
由条件可知 (a-1)n 2 (3a-6)n-8<0恒成立即可满足条件设
f (n) = (a-1)n 2 3(a-2)n-8 (11分)
a = 1时, f (n) = -3n-8<0恒成立
a > 1 时,由二次函数的性质知不可能成立
a < 1 时,对称轴 - EQ \F(3,2) · EQ \F(a-2,a-1) = - EQ \F(3,2) (1- EQ \F(1,a-1) )<0
f (n) 在 (-¥,1] 为单调递减函数.
f (1) = (a-1)n 2 (3a-6)n-8 = (a-1) (3a-6)-8 = 4a-15<0
∴ a < EQ \F(15,4) ∴a < 1 时 4aSn<b恒成立
综上知:a≤1时,4aSn < b 恒成立(14分)
|