|
三角函数式的化简与求值
三角函数式的化简和求值是高考考查的重点内容之一.通过本节的学习使考生把握化简和求值问题的解题规律和途径,非凡是要把握化简和求值的一些常规技巧,以优化我们的解题效果,做到事半功倍.
●难点磁场
(★★★★★)已知 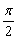 <β<α<
<β<α< 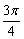 ,cos(α-β)=
,cos(α-β)= 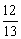 ,sin(α β)=-
,sin(α β)=- 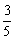 ,求sin2α的值_________.
,求sin2α的值_________.
●案例探究
[例1]不查表求sin220° cos280° 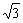 cos20°cos80°的值.
cos20°cos80°的值.
命题意图:本题主要考查两角和、二倍角公式及降幂求值的方法,对计算能力的要求较高.属于★★★★级题目.
知识依托:熟知三角公式并能灵活应用.
错解分析:公式不熟,计算易出错.
技巧与方法:解法一利用三角公式进行等价变形;解法二转化为函数问题,使解法更简单更精妙,需认真体会.
解法一:sin220° cos280° 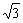 sin220°cos80°
sin220°cos80°
=  (1-cos40°)
(1-cos40°)  (1 cos160°)
(1 cos160°) 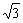 sin20°cos80°
sin20°cos80°
=1-  cos40°
cos40°  cos160°
cos160° 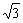 sin20°cos(60° 20°)
sin20°cos(60° 20°)
=1-  cos40°
cos40°  (cos120°cos40°-sin120°sin40°)
(cos120°cos40°-sin120°sin40°) 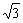 sin20°(cos60°cos20°-sin60°sin20°)
sin20°(cos60°cos20°-sin60°sin20°)
=1-  cos40°-
cos40°- 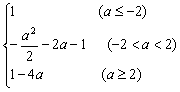 cos40°-
cos40°- 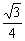 sin40°
sin40° 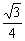 sin40°-
sin40°- 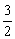 sin220°
sin220°
=1- 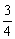 cos40°-
cos40°- 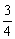 (1-cos40°)=
(1-cos40°)= 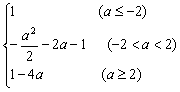
解法二:设x=sin220° cos280° 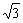 sin20°cos80°
sin20°cos80°
y=cos220° sin280°- 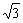 cos20°sin80°,则
cos20°sin80°,则
x y=1 1- 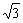 sin60°=
sin60°=  ,x-y=-cos40° cos160°
,x-y=-cos40° cos160° 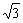 sin100°
sin100°
=-2sin100°sin60° 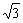 sin100°=0
sin100°=0
∴x=y= 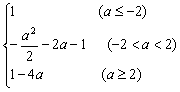 ,即x=sin220° cos280°
,即x=sin220° cos280° 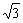 sin20°cos80°=
sin20°cos80°= 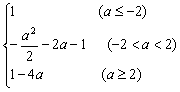 .
.
[例2]设关于x的函数y=2cos2x-2acosx-(2a 1)的最小值为f(a),试确定满足f(a)=  的a值,并对此时的a值求y的最大值.
的a值,并对此时的a值求y的最大值.
命题意图:本题主要考查最值问题、三角函数的有界性、计算能力以及较强的逻辑思维能力.属★★★★★级题目
知识依托:二次函数在给定区间上的最值问题.
错解分析:考生不易考查三角函数的有界性,对区间的分类易出错.
技巧与方法:利用等价转化把问题化归为二次函数问题,还要用到配方法、数形结合、分类讲座等.
解:由y=2(cosx- 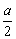 )2-
)2- 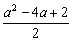 及cosx∈[-1,1]得:
及cosx∈[-1,1]得:
f(a) 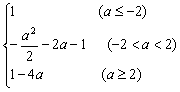
∵f(a)=  ,∴1-4a=
,∴1-4a= 
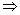 a=
a= 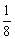
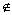 [2, ∞
[2, ∞ 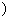
故- 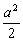 -2a-1=
-2a-1=  ,解得:a=-1,此时,
,解得:a=-1,此时,
y=2(cosx  )2
)2  ,当cosx=1时,即x=2kπ,k∈Z,ymax=5.
,当cosx=1时,即x=2kπ,k∈Z,ymax=5.
[例3]已知函数f(x)=2cosxsin(x 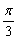 )-
)- 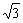 sin2x sinxcosx
sin2x sinxcosx
(1)求函数f(x)的最小正周期;
(2)求f(x)的最小值及取得最小值时相应的x的值;
(3)若当x∈[ 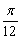 ,
, 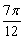 ]时,f(x)的反函数为f-1(x),求f--1(1)的值.
]时,f(x)的反函数为f-1(x),求f--1(1)的值.
命题意图:本题主要考查三角公式、周期、最值、反函数等知识,还考查计算变形能力,综合运用知识的能力,属★★★★★级题目.
知识依托:熟知三角函数公式以及三角函数的性质、反函数等知识.
错解分析:在求f--1(1)的值时易走弯路.
技巧与方法:等价转化,逆向思维.
解:(1)f(x)=2cosxsin(x 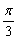 )-
)- 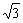 sin2x sinxcosx
sin2x sinxcosx
=2cosx(sinxcos 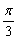 cosxsin
cosxsin 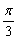 )-
)- 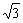 sin2x sinxcosx
sin2x sinxcosx
=2sinxcosx 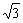 cos2x=2sin(2x
cos2x=2sin(2x 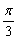 )
)
∴f(x)的最小正周期T=π
(2)当2x 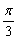 =2kπ-
=2kπ- 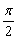 ,即x=kπ-
,即x=kπ- 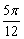 (k∈Z)时,f(x)取得最小值-2.
(k∈Z)时,f(x)取得最小值-2.
(3)令2sin(2x 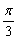 )=1,又x∈[
)=1,又x∈[ 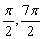 ],
],
∴2x 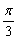 ∈[
∈[ 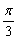 ,
, 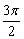 ],∴2x
],∴2x 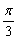 =
= 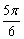 ,则
,则
x= 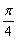 ,故f--1(1)=
,故f--1(1)= 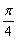 .
.
●锦囊妙计
本难点所涉及的问题以及解决的方法主要有:
1.求值问题的基本类型:1°给角求值,2°给值求值,3°给式求值,4°求函数式的最值或值域,5°化简求值.
2.技巧与方法:
1°要寻求角与角关系的非凡性,化非特角为非凡角,熟练准确地应用公式.
2°注重切割化弦、异角化同角、异名化同名、角的变换等常规技巧的运用.
3°对于条件求值问题,要认真寻找条件和结论的关系,寻找解题的突破口,很难入手的问题,可利用分析法.
4°求最值问题,常用配方法、换元法来解决.
●歼灭难点练习
一、选择题
1.(★★★★★)已知方程x2 4ax 3a 1=0(a>1)的两根均tanα、tanβ,且α,β∈
(- 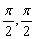 ),则tan
),则tan 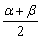 的值是( )
的值是( )
A.  B.-2 C.
B.-2 C. 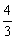 D.
D.  或-2
或-2
二、填空题
2.(★★★★)已知sinα= 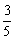 ,α∈(
,α∈( 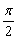 ,π),tan(π-β)=
,π),tan(π-β)=  ,则tan(α-2β)=_________.
,则tan(α-2β)=_________.
3.(★★★★★)设α∈( 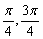 ),β∈(0,
),β∈(0, 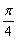 ),cos(α-
),cos(α- 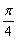 )=
)= 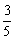 ,sin(
,sin( 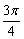 β)=
β)= 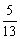 ,则sin(α β)=_________.
,则sin(α β)=_________.
三、解答题
4.不查表求值: 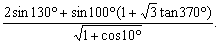
5.已知cos( 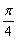 x)=
x)= 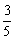 ,(
,( 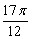 <x<
<x< 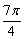 ),求
),求 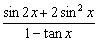 的值.
的值.
6.(★★★★★)已知α-β= 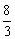 π,且α≠kπ(k∈Z).求
π,且α≠kπ(k∈Z).求 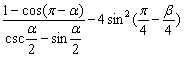 的最大值及最大值时的条件.
的最大值及最大值时的条件.
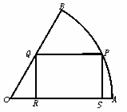 7.(★★★★★)如右图,扇形OAB的半径为1,中心角60°,四边形PQRS是扇形的内接矩形,当其面积最大时,求点P的位置,并求此最大面积. 7.(★★★★★)如右图,扇形OAB的半径为1,中心角60°,四边形PQRS是扇形的内接矩形,当其面积最大时,求点P的位置,并求此最大面积.
8.(★★★★★)已知cosα sinβ= 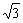 ,sinα cosβ的取值范围是D,x∈D,求函数y=
,sinα cosβ的取值范围是D,x∈D,求函数y= 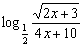 的最小值,并求取得最小值时x
的最小值,并求取得最小值时x
的值.
参考答案
难点磁场
解法一:∵ 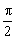 <β<α<
<β<α< 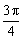 ,∴0<α-β<
,∴0<α-β< 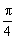 .π<α β<
.π<α β< 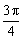 ,
,
∴sin(α-β)= 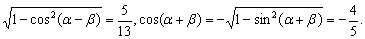
∴sin2α=sin[(α-β) (α β)]
=sin(α-β)cos(α β) cos(α-β)sin(α β)
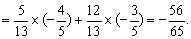
解法二:∵sin(α-β)= 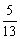 ,cos(α β)=-
,cos(α β)=- 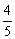 ,
,
∴sin2α sin2β=2sin(α β)cos(α-β)=- 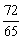
sin2α-sin2β=2cos(α β)sin(α-β)=- 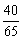
∴sin2α= 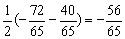
歼灭难点练习
一、1.解析:∵a>1,tanα tanβ=-4a<0.
tanα tanβ=3a 1>0,又α、β∈(- 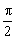 ,
, 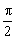 )∴α、β∈(-
)∴α、β∈(- 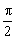 ,θ),则
,θ),则 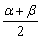 ∈(-
∈(- 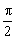 ,0),又tan(α β)=
,0),又tan(α β)=  ,
,
整理得2tan2  =0.解得tan
=0.解得tan 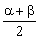 =-2.
=-2.
答案:B
2.解析:∵sinα= 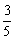 ,α∈(
,α∈( 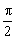 ,π),∴cosα=-
,π),∴cosα=- 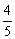
则tanα=- 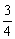 ,又tan(π-β)=
,又tan(π-β)=  可得tanβ=-
可得tanβ=-  ,
,
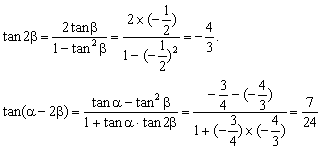
答案: 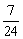
3.解析:α∈( 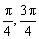 ),α-
),α- 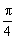 ∈(0,
∈(0, 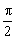 ),又cos(α-
),又cos(α- 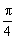 )=
)= 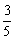 .
.
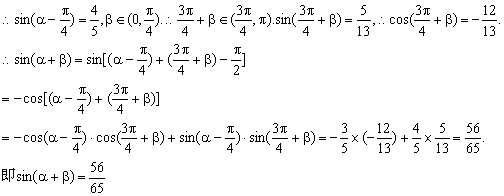
答案: 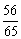
三、4.答案:2
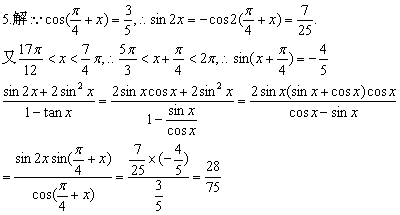
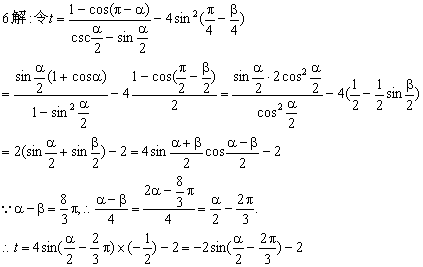
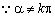 (k∈Z),
(k∈Z), 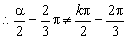 (k∈Z)
(k∈Z)
∴当  即
即 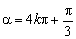 (k∈Z)时,
(k∈Z)时, 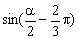 的最小值为-1.
的最小值为-1.
7.解:以OA为x轴.O为原点,建立平面直角坐标系,并设P的坐标为(cosθ,sinθ),则
|PS|=sinθ.直线OB的方程为y= 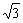 x,直线PQ的方程为y=sinθ.联立解之得Q(
x,直线PQ的方程为y=sinθ.联立解之得Q( 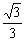 sinθ;sinθ),所以|PQ|=cosθ-
sinθ;sinθ),所以|PQ|=cosθ- 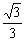 sinθ.
sinθ.
于是SPQRS=sinθ(cosθ- 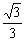 sinθ)=
sinθ)= 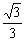 (
( 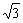 sinθcosθ-sin2θ)=
sinθcosθ-sin2θ)= 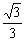 (
( 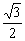 sin2θ-
sin2θ- 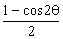 )=
)= 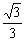 (
( 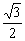 sin2θ
sin2θ  cos2θ-
cos2θ-  )=
)= 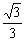 sin(2θ
sin(2θ 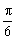 )-
)- 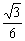 .
.
∵0<θ< 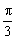 ,∴
,∴ 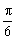 <2θ
<2θ 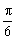 <
< 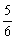 π.∴
π.∴  <sin(2θ
<sin(2θ 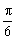 )≤1.
)≤1.
∴sin(2θ 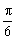 )=1时,PQRS面积最大,且最大面积是
)=1时,PQRS面积最大,且最大面积是 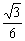 ,此时,θ=
,此时,θ= 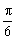 ,点P为
,点P为 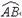 的中点,P(
的中点,P( 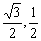 ).
).
8.解:设u=sinα cosβ.则u2 ( 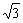 )2=(sinα cosβ)2 (cosα sinβ)2=2 2sin(α β)≤4.∴u2≤1,-1≤u≤1.即D=[-1,1],设t=
)2=(sinα cosβ)2 (cosα sinβ)2=2 2sin(α β)≤4.∴u2≤1,-1≤u≤1.即D=[-1,1],设t= 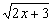 ,∵-1≤x≤1,∴1≤t≤
,∵-1≤x≤1,∴1≤t≤ 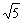 .x=
.x=  .
.
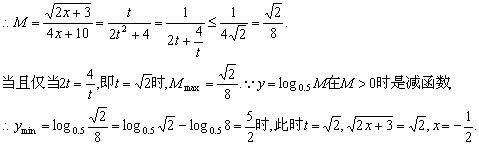
|