|
高考数学第二次练兵考试试题
数学(理科)
本试卷分为第Ⅰ卷(试题卷)和第Ⅱ卷(答题卷)两部分。共150分,考试时间120分钟.本次考试只交答题卷。
第Ⅰ卷(试题卷)
一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项符合要求的.
1. 设集合 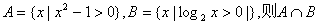 等于
等于
A. 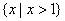 B.
B. 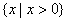 C.
C. 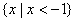 D.
D. 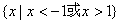
2.  等于
等于
A.  B.
B.  C.
C.  D.
D. 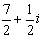
3. 下列函数中,最小正周期为 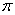 ,且图象关于直线
,且图象关于直线 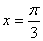 对称的是
对称的是
A. 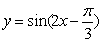 B.
B. 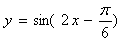 C.
C. 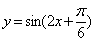 D.
D. 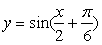
4. 下列所给4个图象中,与所给3件事吻合顺序最好的为
(1)我离开家不久,发现自己把作业本忘在家里了,于是马上返回家里取了作业本再上学;
(2)我骑着车一路以常速行驶,只是在途中碰到一次交通堵塞,耽搁了一些时间;
 (3)我出发后,心情轻松,缓缓行进,后来为了赶时间开始加速。 (3)我出发后,心情轻松,缓缓行进,后来为了赶时间开始加速。
A、(1)(2)(4) B、(4)(2)(3) C、(4)(1)(2) D、(4)(1)(3)
5. 在等比数列  中,已知
中,已知  是关于
是关于 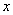 方程
方程 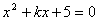 的两个根,则
的两个根,则 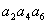 等于
等于
(A)  (B)25 (C)
(B)25 (C)  (D)
(D) 
|
a = 1
b = 2
c = 3
a = b
b = c
c = a
PRINT a,b,c
END
(第6题) |  6. 右边程序运行的结果是 6. 右边程序运行的结果是
A.1,2,3 B. 3,2,1 C. 2,3,1 D2,3,2
7. 已知函数f(x)=x3 ax2,点P(-1,b)在曲线y=f(x) 上,
则以P为切点且平行于直线3x y=0的切线方程为
A.3x y-1=0 B.3x y-2=0
C.3x-y+1=0 D.3x y 1=0
8. 定义运算 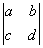 =ad-bc,则符合条件
=ad-bc,则符合条件  =0
=0
的点P(x,y)的轨迹方程为
A. (x-1)2 4y2=1 B.(x-1)2-4y2=1 C.(x-1)2 y2=1 D.(x-1)2-y2=1
二、填空题:本大题共7小题,每小题5分,满分30分,其中13~15题是选做题,考生只能选做二题,三题全答的,只计算前两题得分.
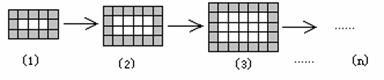
9. 下图是用同样规格的黑、白两色正方形瓷砖铺设的若干图案,则按此规律第n个图案中需用黑色瓷砖___________块.(用含n的代数式表示)
10.若向量  满足
满足 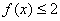 与
与 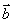 的夹角为120°,则
的夹角为120°,则 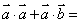 .
.
11. 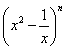 的展开式中,常数项为
的展开式中,常数项为  ,则
,则  _____ ____________.
_____ ____________.
12. 等体积的球和正方体,它们的表面积的大小关系是  _____
_____  .
.
(填”大于、小于或等于”).
13.(坐标系与参数方程选做题).已知点 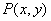 在曲线
在曲线 
 (
( 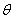 为参数)上,则
为参数)上,则 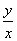 的取值范围为 .
的取值范围为 .
14.(不等式选讲选做题)设函数 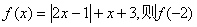 = ;若
= ;若 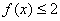 ,则
,则 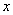 的取值范围是 .
的取值范围是 .
 15.(几何证实选讲选做题)如图, AC为⊙O的直径,BD⊥AC于P,PC=2,PA=8 15.(几何证实选讲选做题)如图, AC为⊙O的直径,BD⊥AC于P,PC=2,PA=8
则CD的长为 、cos∠ACB= .(用数字表示)
三、解答题:本大题共有6小题,满分80分.解答须写出文字说明、证实过程和演算步骤.
16.(本小题满分12分)
在△ABC中,a= 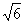 ,b=2,c=
,b=2,c= 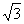 1,求A、B、C及S△ABC.
1,求A、B、C及S△ABC.
17.(本题满分12分)
已知数列 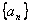 的前n项和
的前n项和 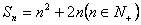
(Ⅰ)求通项  ;
;
(Ⅱ)求和: 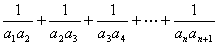
18.(本小题满分14分)
已知某椭圆的焦点是 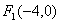 、
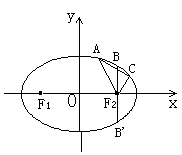
、  ,过点F2并垂直于x轴的直线与椭圆的一个交点为B,且
,过点F2并垂直于x轴的直线与椭圆的一个交点为B,且  ,椭圆上不同的两点
,椭圆上不同的两点 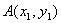 、
、 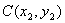 满足条件:
满足条件: 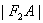 、
、 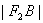 、
、 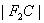 成等差数列.
成等差数列.
(I)求该椭圆的方程;
(II)求弦AC中点的横坐标.
19.(本小题满分14分)
在直三棱柱ABC—A1B1C1中,CA=CB=CC1=2,∠ACB=90°,E、F分别是BA、BC的中点,G是AA1上一点,且AC1⊥EG.
(Ⅰ)确定点G的位置;
(Ⅱ)求直线AC1与平面EFG所成角θ的大小.
20.(本小题满分14分)
甲、乙、丙三个口袋内都分别装有6个不相同的球,并且每个口袋内的6个球均有1个红球,2个黑球,3个无色透明的球,现从甲、乙、丙三个口袋中依次随机各摸出1个球.
(1)求恰好摸出红球、黑球和无色球各1个的概率;
(2)求摸出的3个球中含有有色球数ξ的概率分布列和数学期望.
21.(本小题满分14分)
已知函数 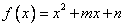 的图像过点
的图像过点  ,且
,且  对任意实数都成立,函数
对任意实数都成立,函数 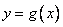 与
与  的图像关于原点对称。
的图像关于原点对称。
⑴ 求 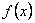 与
与  的解析式;
的解析式;
⑵ 若 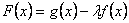 在[-1,1]上是增函数,求实数λ的取值范围;
在[-1,1]上是增函数,求实数λ的取值范围;
|