|
一、填空题(本题共14题,每题5分,共70分,请将正确答案填写在答题试卷上)
1、已知 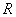 为实数集,
为实数集, 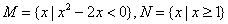 ,则
,则  .
.
2、若复数 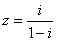 ,则
,则 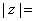 .
.
3、已知0<a<1,  ,则
,则 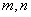 与1三者的大小关系是 .
与1三者的大小关系是 .
4、如图(下面),一个简单空间几何体的三视图其主视图与左视图是边长为2的正三角形、俯视图轮廓为正方形,则其体积是 .
5、设a、b、c分别是△ABC中∠A、∠B、∠C所对边的边长,则直线 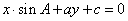 与
与 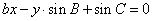 的位置关系是 .
的位置关系是 .
6、已知a与b均为单位向量,它们的夹角为60º,那么| a 3b |等于 .
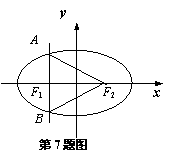
7、如图(下面)已知点F1、F2分别是椭圆 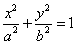 的左、右焦点,过F1且垂直于x轴的直线与椭圆交于A、B两点,若△ABF2为正三角形,则该椭圆的离心率
的左、右焦点,过F1且垂直于x轴的直线与椭圆交于A、B两点,若△ABF2为正三角形,则该椭圆的离心率  是 .
是 .
8、已知函数  ,则方程
,则方程 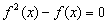 的实根共有 .
的实根共有 .
9、假如数据x1、x2、…、xn 的平均值为 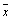 ,方差为S2 ,则3x1 5、3x2 5、…、3xn 5 的方差为 .
,方差为S2 ,则3x1 5、3x2 5、…、3xn 5 的方差为 .
10、若抛物线  的焦点与椭圆
的焦点与椭圆 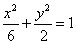 的右焦点重合,则
的右焦点重合,则 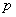 的值为 .
的值为 .
11、设奇函数  在
在 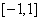 上是增函数,且
上是增函数,且 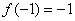 .若函数,
.若函数, 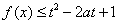 对所有的
对所有的 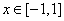 都成立,则当
都成立,则当 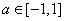 时,
时, 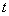 的取值范围是 .
的取值范围是 .
12、考察下列一组不等式:
 .
.
将上述不等式在左右两端仍为两项和的情况下加以推广,使以上的不等式成为推广不等式的特例,则推广的不等式可以是___________________.
13、若框图所给的程序运行的结果为S=132,那么判定框中
应填入的关于k的判定条件是 .
14、等差数列  的前
的前 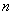 项和为
项和为  ,公差
,公差 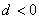 . 若存在正整数
. 若存在正整数 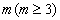 ,使得
,使得  ,则当
,则当 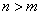 (
( 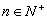 )时,有
)时,有  (填“>”、“<”、“=”).
(填“>”、“<”、“=”).


.
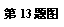
答题试卷 班级 姓名 学号
一、填空题(本题共14题,每题5分,共70分)
1. 2. 3. 4. 5. 6. 7.
8. 9. 10. 11.
12.
13. 14.
二、解答题(本题6大题,共90分)
15.(本小题满分14分)
已知:  ,
, 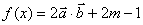 (
( 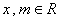 ).
).
(1) 求  关于
关于 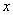 的表达式,并求
的表达式,并求  的最小正周期;
的最小正周期;
(2) 若 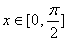 时
时  的最小值为5,求
的最小值为5,求 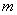 的值.
的值.
16.(本小题满分14分)
在平面直角坐标系 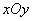 ,已知圆心在第二象限、半径为
,已知圆心在第二象限、半径为 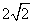 的圆
的圆 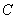 与直线
与直线  相切于坐标原点
相切于坐标原点 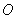 .椭圆
.椭圆 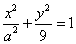 与圆
与圆 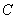 的一个交点到椭圆两焦点的距离之和为
的一个交点到椭圆两焦点的距离之和为 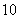 .
.
(1)求圆 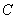 的方程;
的方程;
(2)试探究圆 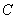 上是否存在异于原点的点
上是否存在异于原点的点  ,使
,使  到椭圆右焦点
到椭圆右焦点 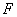 的距离等于线段
的距离等于线段  的长,若存在,请求出点
的长,若存在,请求出点  的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
17.(本小题满分14分)
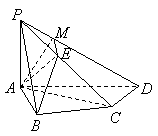
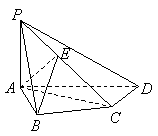 如图,在四棱锥 如图,在四棱锥  中,
中,  底面
底面  ,
, 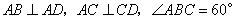 ,
,  ,
,  是
是  的中点.
的中点.
(1)证实  ;
;
(2)证实 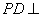 平面
平面  ;
;
18、(本小题满分14分)
设数列 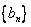 的前
的前 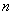 项和为
项和为  ,且
,且  ;数列
;数列  为等差数列,且
为等差数列,且 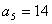 ,
,  .
.
(1)求数列 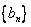 的通项公式;
的通项公式;
(2)若 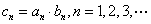 ,
,  为数列
为数列 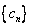 的前
的前 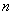 项和. 求证:
项和. 求证: 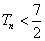 .
.
19.(本小题满分16分)
某商品每件成本9元,售价为30元,每星期卖出432件,假如降低价格,销售量可以增加,且每星期多卖出的商品件数与商品单价的降低值 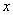 (单位:元,
(单位:元,  )的平方成正比,已知商品单价降低2元时,一星期多卖出24件.
)的平方成正比,已知商品单价降低2元时,一星期多卖出24件.
(1)将一个星期的商品销售利润表示成 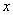 的函数;
的函数;
(2)如何定价才能使一个星期的商品销售利润最大?
20.(本小题满分18分)
已知函数 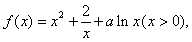
(1) 若  在
在  上单调递增,求
上单调递增,求 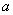 的取值范围;
的取值范围;
(2) 若定义在区间D上的函数 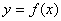 对于区间D上的任意两个值
对于区间D上的任意两个值 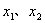 总有以下不等式
总有以下不等式  成立,则称函数
成立,则称函数 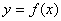 为区间D上的“凹函数”.
为区间D上的“凹函数”.
试证当  时,
时,  为“凹函数”.
为“凹函数”.
高三数学模拟试题 班级 姓名 学号
附加题(理科考生做,本大题共4题,满分40分.考试时间30分钟)
21.(本题10分) 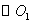 和
和 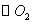 的极坐标方程分别为
的极坐标方程分别为 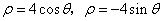 .
.
(1)把 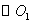 和
和 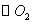 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)求经过 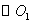 ,
, 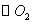 交点的直线的直角坐标方程.
交点的直线的直角坐标方程.
22.(本题10分)
已知实数 
 满足
满足  ,
, 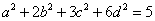 .试求实数
.试求实数 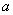 的取值范围.
的取值范围.
23.(本小题满分10分)
某陶瓷厂预备烧制甲、乙、丙三件不同的工艺品,制作过程必须先后经过两次烧制,当第一次烧制合格后方可进入第二次烧制,两次烧制过程相互独立.根据该厂现有的技术水平,经过第一次烧制后,甲、乙、丙三件产品合格的概率依次为  ,
, 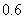 ,
, 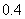 ,经过第二次烧制后,甲、乙、丙三件产品合格的概率依次为
,经过第二次烧制后,甲、乙、丙三件产品合格的概率依次为 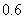 ,
,  ,
, 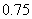 .
.
(1)求第一次烧制后恰有一件产品合格的概率;
(2)经过前后两次烧制后,合格工艺品的个数为  ,求随机变量
,求随机变量  的期望.
的期望.
24.(本小题满分10分)
 右图是一个直三棱柱(以 右图是一个直三棱柱(以  为底面)被一平面所截得到的几何体,截面为
为底面)被一平面所截得到的几何体,截面为 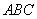 .已知
.已知 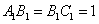 ,
, 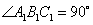 ,
,  ,
,  ,
,  .
.
(1)设点 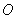 是
是 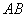 的中点,证实:
的中点,证实: 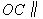 平面
平面  ;
;
(2)求二面角 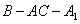 的大小;
的大小;
(3)求此几何体的体积.
数学试题参考答案和评分标准
一、填空题(每题5分,共70分)
1.  2.
2.  3. 1<n<m 4.
3. 1<n<m 4. 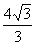 5. 垂直 6.
5. 垂直 6. 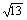 7.
7. 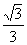
8. 7个 9. 9S2 10. 4 11. 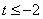 或
或  或
或 
12. 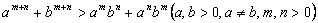 (或
(或 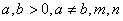 为正整数).注:
为正整数).注:
填 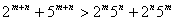 以及是否注明字母的取值符号和关系,均不扣分;
以及是否注明字母的取值符号和关系,均不扣分;
若填 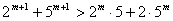 或
或 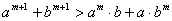 可给3分.
可给3分.
13. 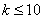 . 14.<
. 14.<
二、解答题(共90分)
15. 解:(1) 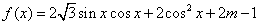 ……………………………………………………2分
……………………………………………………2分
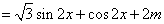 ………………………………………………………………………………………………4分
………………………………………………………………………………………………4分
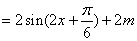 . …………………………………………………………………………………………………………6分
. …………………………………………………………………………………………………………6分
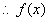 的最小正周期是
的最小正周期是 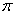 . …………………………………………………………………………………………………7分
. …………………………………………………………………………………………………7分
(2) ∵  ,∴
,∴ 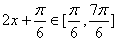 …………………………………………………………………8分
…………………………………………………………………8分
∴当  即
即 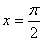 时,函数
时,函数  取得最小值是
取得最小值是  . ………………………10分
. ………………………10分
∵ 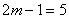 ,∴
,∴  . …………………………………………………………………………………………………12分
. …………………………………………………………………………………………………12分
16.解析:(1)圆C: 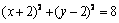 ;………………………………………………………………6分
;………………………………………………………………6分
(2)由条件可知a=5,椭圆  ,∴F(4,0),若存在,则F在OQ的中垂线上,又O、Q在圆C上,所以O、Q关于直线CF对称;
,∴F(4,0),若存在,则F在OQ的中垂线上,又O、Q在圆C上,所以O、Q关于直线CF对称;
直线CF的方程为y-1= 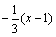 ,即
,即 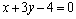 ,设Q(x,y),则
,设Q(x,y),则  ,解得
,解得 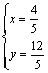
所以存在,Q的坐标为 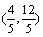 .…………………………………………14分
.…………………………………………14分
17. (1)证实:在四棱锥  中,因
中,因  底面
底面  ,
,  平面
平面 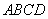 ,故
,故 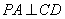 .
.
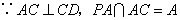 ,
,  平面
平面 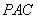 .
.
 而 而  平面
平面  ,
,  .
.
(Ⅱ)证实:由  ,
, 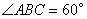 ,可得
,可得  .
.
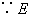 是
是  的中点,
的中点, 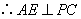 .
.
由(1)知, 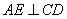 ,且
,且 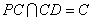 ,所以
,所以 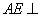 平面
平面 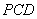 .
.
而 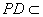 平面
平面 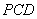 ,
, 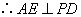 .
.
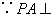 底面
底面  在底面
在底面 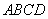 内的射影是
内的射影是  ,
, 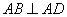 ,
, 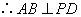 .
.
又 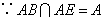 ,综上得
,综上得 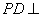 平面
平面  .
.
(3)(课后加):过点 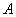 作
作 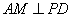 ,垂足为
,垂足为  ,连结
,连结 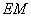 .则(Ⅱ)知,
.则(Ⅱ)知, 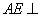 平面
平面 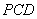 ,
, 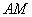 在平面
在平面 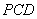 内的射影是
内的射影是 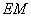 ,则
,则 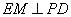 .
.
因此  是二面角
是二面角  的平面角.
的平面角.
由已知,得 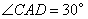 .设
.设 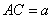 ,
,
可得 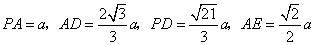 .
.
在 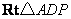 中,
中,  ,
, 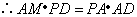 ,
,
则 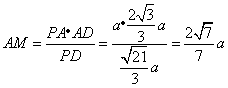 .在
.在  中,
中, 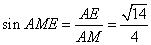 .
.
所以二面角  的大小是
的大小是 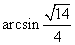 .
.
18. 解:(1)由 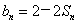 ,令
,令 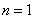 ,则
,则  ,又
,又 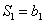 ,所以
,所以  .
.
 ,则
,则  . ……………………………………………………………………………………2分
. ……………………………………………………………………………………2分
当 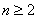 时,由
时,由 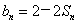 ,可得
,可得 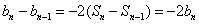 .
.
即  . …………………………………………………………………………………………………………………………4分
. …………………………………………………………………………………………………………………………4分
所以 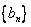 是以
是以  为首项,
为首项, 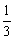 为公比的等比数列,于是
为公比的等比数列,于是 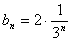 . …………5分
. …………5分
(2)数列  为等差数列,公差
为等差数列,公差 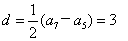 ,可得
,可得 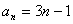 . ………………7分
. ………………7分
从而 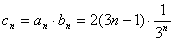 . ……………………………………………………………………………………8分
. ……………………………………………………………………………………8分
∴ 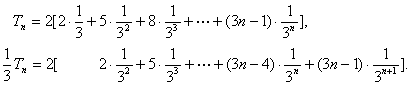 ……………10分
……………10分
∴ 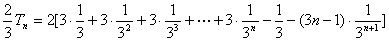 . …………………11分
. …………………11分
从而 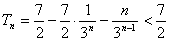 . …………………………………………………………………………14分
. …………………………………………………………………………14分
19.解:(1)设商品降价 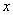 元,则多卖的商品数为
元,则多卖的商品数为 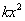 ,若记商品在一个星期的获利为
,若记商品在一个星期的获利为  ,
,
则依题意有  ,
,
又由已知条件,  ,于是有
,于是有  ,
,
所以 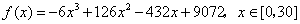 .
.
(2)根据(1),我们有 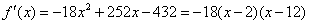 .
. |
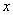
|
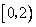
|
2 |
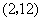
|
12 |

| |
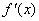
|
|
0 |
|
0 |
| |

|

|
极小 |

|
极大 |

| |  (1)证实:作
(1)证实:作 