|
高考数学理科实验班仿真试题
本试卷分第Ⅰ卷(选择题 共50分)和第Ⅱ卷(非选择题 共100分),考试时间为120分钟,满分为150分.
第Ⅰ卷(选择题 共50分)
一、选择题(本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的,答案涂在答题卡上)
1.如图所示是2008年北京奥运会的会徽,其中的“中国印”由四个色块构成,可以用线段在不穿越其他色块的条件下将其中任意两个色块连接起来(如同架桥),假如用三条线段将这四个色块连接起来,不同的连接方法共有( )

A.8种 B.12种 C.16种 D.20种1. 函数2. 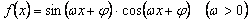 以2为最小正周期,且能在x=2时取得最大值,则φ的一个值是 ( )
以2为最小正周期,且能在x=2时取得最大值,则φ的一个值是 ( )
A、 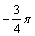 B、
B、 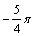 C、
C、  D、
D、 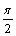
3. .给出下列四个命题:
①有两个面平行,其余各面都是平行四边形的几何体是棱柱;
②有两侧面与底面垂直的棱柱是直棱柱;
③过斜棱柱的侧棱作棱柱的截面,所得图形不可能是矩形;
④所有侧面都是全等的矩形的四棱柱一定是正四棱柱。
其中正确的命题的个数为( )个
A、 0 B 、 1 C、 2 D、 3
4.满足不等式 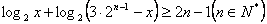 的正整数
的正整数  的个数记为
的个数记为  ,数列
,数列  的前
的前  项和记为
项和记为 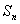 ,则
,则 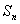
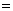 ( )
( )
A. 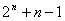 B.
B.  C.
C. 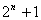 D.
D. 
5.如图2所示,面积为S的平面凸四边形的第 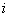 条边的边长记为
条边的边长记为 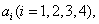 此四边形内任一点P到第
此四边形内任一点P到第 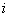 条边的距离记为
条边的距离记为  ,若
,若 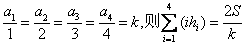 .类比以上性质,体积为V三棱锥的第
.类比以上性质,体积为V三棱锥的第 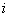 个面的面积记为
个面的面积记为 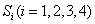 ,此三棱锥内任一点Q到第
,此三棱锥内任一点Q到第 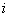 个面的距离记为
个面的距离记为 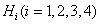 ,
,
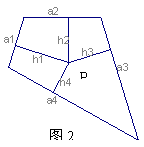 若 若  ( )
( )
A.  B.
B. 
C. 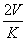 D.
D. 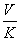
 6.设U为全集,M、P是U的两个子集,且 6.设U为全集,M、P是U的两个子集,且 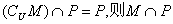 等于 ( )
等于 ( )
A.M B.P C.CUP D.○
7.若函数y=f(x 1)的定义域是[-2,3],则y=f(2x-1)的定义域为( )
A.[0, 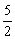 ] B.[-1,4] C.[-5,5] D.[-3,7]
] B.[-1,4] C.[-5,5] D.[-3,7]
8.若三点 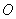 、
、 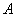 、
、  不共线,则“存在唯一一对实数
不共线,则“存在唯一一对实数 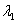 、
、 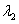 ,使
,使 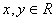 ”是“
”是“ 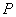 点在直线
点在直线  上”的( )
上”的( )
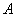 .充分不必要条件
.充分不必要条件  .必要不充分条件
.必要不充分条件
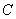 .充要条件
.充要条件 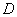 .既不充分也不必要条件
.既不充分也不必要条件
9.在等差数列  中,若
中,若  ,则
,则 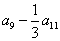 的值为 ( )
的值为 ( )
A.14 B.15 C.16 D.17
10.已知椭圆  与双曲线
与双曲线 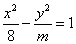 有相同的准线,则动点
有相同的准线,则动点 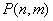 的轨迹为( )
的轨迹为( )
A.椭圆的一部分 B.双曲线的一部分
C.抛物线的一部分 D.直线的一部分
二、填空题
11.已知正方体 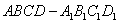 ,
, 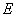 为
为 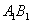 的中点,则异面直线
的中点,则异面直线 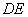 与
与 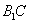 所成角的余弦是 .
所成角的余弦是 .
12. .已知x,y满足条件  ,则z=x 3y 1的取值范围
,则z=x 3y 1的取值范围
13. 如图,半径为2的半球内有一内接正六棱锥
 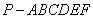 ,则此正六棱锥的侧面积是________.
,则此正六棱锥的侧面积是________.
14.设命题  :
: 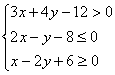 (
( 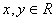 ),命题
),命题  :
: 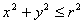 (
( 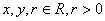 ),若命题
),若命题  是命题
是命题 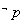 的充分非必要条件,则
的充分非必要条件,则 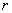 的取值范围是 .
的取值范围是 .
15.已知双曲线 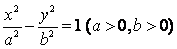 的离心率为
的离心率为  , 若它的一条准线与抛物线
, 若它的一条准线与抛物线 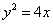 的准线重合.设双曲线与抛物线的一个交点为
的准线重合.设双曲线与抛物线的一个交点为 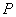 ,抛物线的焦点为
,抛物线的焦点为 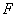 ,则
,则 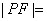 .
.
16.非空集合M关于运算 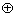 满足:(1)对任意的a,
满足:(1)对任意的a, 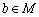 ,都有
,都有 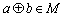 ;(2)存在
;(2)存在 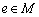 ,使得对一切
,使得对一切 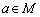 ,都有
,都有 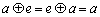 ,则称M关于运算
,则称M关于运算 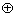 为“理想集”.
为“理想集”.
现给出下列集合与运算:
①M={非负整数}, 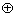 为整数的加法;②M={偶数},
为整数的加法;②M={偶数}, 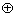 为整数的乘法;
为整数的乘法;
③M={二次三项式}, 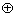 为多项式的加法;④M={平面向量},
为多项式的加法;④M={平面向量}, 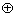 为平面向量的加法;
为平面向量的加法;
其中M关于运算 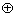 为“理想集”的是 .(只需填出相应的序号)
为“理想集”的是 .(只需填出相应的序号)
三、解答题
17.(本小题满分12分)
已知向量  =(
=( 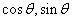 ),
),  =(
=(  ),
), 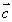 =(-1,0),
=(-1,0), 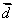 =(0,1).
=(0,1).
(1)求证:  ⊥(
⊥( 
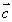 )
) 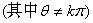 ;
;
(2)设 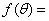
 ·(
·(  -
- 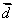 ),且
),且  ,求
,求  的值域.
的值域.
18.(本小题满分14分)
已知直线 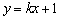 与双曲线
与双曲线 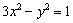 有A、B两个不同的交点.
有A、B两个不同的交点.
(1)假如以AB为直径的圆恰好过原点O,试求k的值;
(2)是否存在k,使得两个不同的交点A、B关于直线  对称?试述理由.
对称?试述理由.
19.(本大题满分14分)如图,在五面体ABCDEF中,四边形ABCD为矩形,对角线AC,BD的交点为O,△ABF和△DEC为等边三角形,棱EF∥BC,EF= eq \f(1,2)BC,AB=1,BC=2,M为EF的中点,
 ①求证:OM⊥平面ABCD; ①求证:OM⊥平面ABCD;
②求二面角E-CD-A的大小;
③求点A到平面CDE的距离。
20.(本小题满分14分)
已知函数 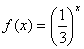 .
.
(1) 若 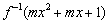 的定义域为
的定义域为 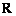 ,求实数
,求实数 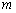 的取值范围;
的取值范围;
(2) 当  时,求函数
时,求函数 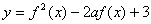 的最小值
的最小值  .
.
(3) 是否存在实数 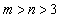 ,使得
,使得  的定义域为
的定义域为 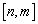 ,值域为
,值域为  ,若存在,求出
,若存在,求出 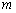 、
、 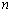 的值;若不存在,则说明理由.
的值;若不存在,则说明理由.
21.过曲线 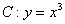 上的点
上的点 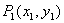 作曲线
作曲线 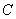 的切线l1与曲线
的切线l1与曲线 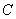 交于点
交于点  ,过点
,过点 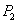 作曲线
作曲线 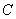 的切线l2与曲线
的切线l2与曲线 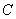 交于点
交于点  ,依此类推,可得到点列:
,依此类推,可得到点列: 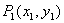 ,
, 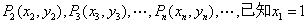 .
.
(1)求点P2、P3的坐标;
(2)求数列  的通项公式;
的通项公式;
(3)记点 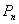 到直线
到直线 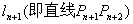 的距离为
的距离为  ,
,
求证: 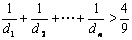 .
.
答 案
一、选择题:CAAAB DABCD
二、填空题
11. 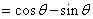 ;12. [1,5]; 13.6
;12. [1,5]; 13.6  ;14. (0,
;14. (0, 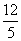 ] ; 15、4;16.① ④.
] ; 15、4;16.① ④.
三、解答题
17.解(1)∵ 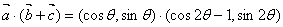
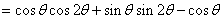 …………………………… 3分
…………………………… 3分
= 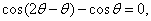
∴ 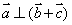 ……………………………………………………………………6分
……………………………………………………………………6分
(2) 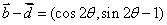 ………………………………………………………7分
………………………………………………………7分
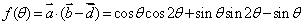 …………………9分
…………………9分
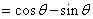 =
= 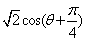
∵ 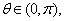 ∴
∴  ∴
∴ 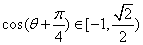
∴  的值域为
的值域为  ……………………12分
……………………12分
18.(本小题满分14分)
解:(1)设  ,则以AB为直径的圆恰好过原点O的充要条件是
,则以AB为直径的圆恰好过原点O的充要条件是 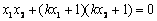 ,即
,即  …①……2分
…①……2分
由 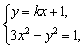 消去y得
消去y得 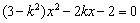 …②
…②
 …………………………5分
…………………………5分
将其代入①得 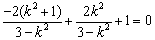 ,解得
,解得 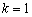 或
或 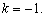
当 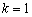 时,方程②为
时,方程②为  ,有两个不等实根;
,有两个不等实根;
当  时,方程②为
时,方程②为  ,有两个不等实根.
,有两个不等实根.
故当 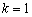 或
或  时,以AB为直径的圆恰好过原点O. ………………8分
时,以AB为直径的圆恰好过原点O. ………………8分
(2)若  关于直线
关于直线  对称,
对称,
则 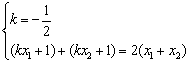 …………………………10分
…………………………10分
将④整理得 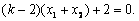 ………………12分
………………12分
因为  所以
所以  ,解之,得
,解之,得 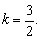 这个结果与③矛盾.
这个结果与③矛盾.
故不存在这样的k,使两点A、B关于直线  对称. ……………………14分
对称. ……………………14分
18.解:( = 1 \* ROMAN I)设P(x,y),因为A、B分别为直线 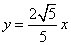 和
和 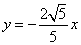 上的点,故可设
上的点,故可设  ,
,  .
.
∵ 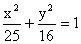 ,
,
∴ 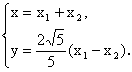 ∴
∴ 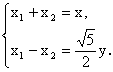 ………………………4分
………………………4分
又 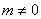 ,
,
∴  .……………………………………5分
.……………………………………5分
∴  .
.
即曲线C的方程为 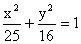 .………………………………………6分
.………………………………………6分
( = 2 \* ROMAN II) 设N(s,t),M(x,y),则由 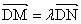 ,可得(x,y-16)=
,可得(x,y-16)= 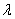 (s,t-16).
(s,t-16).
故  ,
, 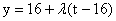 .……………………………………8分
.……………………………………8分
∵M、N在曲线C上,
∴ 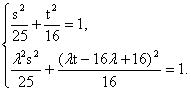 ……………………………………9分
……………………………………9分
消去s得 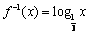 .
.
由题意知 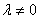 ,且
,且 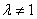 ,
,
解得 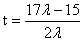 .………………………………………………………12分
.………………………………………………………12分
又 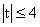 , ∴
, ∴ 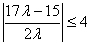 .
.
解得 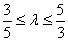 (
( 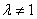 ).
).
故实数 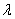 的取值范围是
的取值范围是 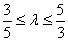 (
( 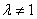 ).………………………………14分
).………………………………14分
19.解:(1) ∵ 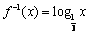 (
( 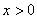 ), ……… 2分
), ……… 2分
∴ 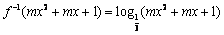 ,由题知,
,由题知,  恒成立,
恒成立,
∴10当  时,
时, 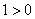 满足题意; ……… 3分
满足题意; ……… 3分
20当 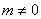 时,应有
时,应有  ,
,
∴实数 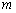 的取值范围为
的取值范围为 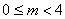 。 ……… 5分
。 ……… 5分
(2) ∵ 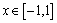 ,∴
,∴ 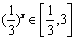 ,
,
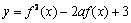
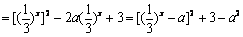 ,……… 7分
,……… 7分
当 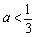 时,
时, 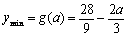 ;
;
当 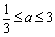 时,
时, 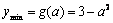 ;
;
当 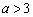 时,
时, 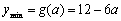 .
.
∴  . …………10分 (错一个扣一分)
. …………10分 (错一个扣一分)
(3) ∵ 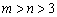 ,∴
,∴ 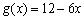 ,在
,在 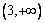 上是减函数.
上是减函数.
∵  的定义域为
的定义域为 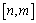 ,值域为
,值域为  ,
,
∴ 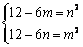 ,
,  …………… 12分
…………… 12分
②-①得: 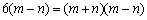 ,
,
∵ 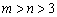 ,∴
,∴ 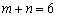 .但这与“
.但这与“ 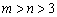 ”矛盾.
”矛盾.
∴满足题意的 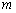 、
、 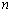 不存在. ………………… 14分
不存在. ………………… 14分
21.解:(1) 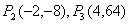 …………………………………………4分
…………………………………………4分
(2)曲线C上点 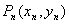 处的切线
处的切线 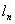 的斜率为
的斜率为 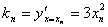 ,
,
故得到切线的方程为 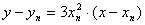 ……………………………………6分
……………………………………6分
联立方程 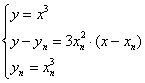 消去y,
消去y,  得:
得: 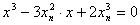
化简得: 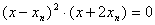 所以:
所以:  ………………8分
………………8分
由  得到点Pn的坐标
得到点Pn的坐标 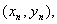 由
由 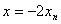 就得到点
就得到点 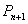 的坐标
的坐标 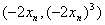 所以:
所以: 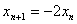 故数列
故数列  为首项为1,公比为-2的等比数列所以:
为首项为1,公比为-2的等比数列所以:  …………………………………………10分
…………………………………………10分
(3)由(2)知: 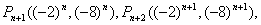
所以直线 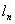 的方程为:
的方程为: 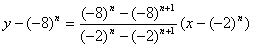
化简得: 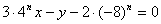 …………………………………………12分
…………………………………………12分

所以  ∴
∴ 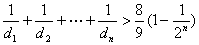 ≥
≥ 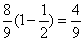 ……16分
……16分
|