|
高考数学一模考试试题(理科)
参考公式:
假如事件  互斥,那幺 球的表面积公式
互斥,那幺 球的表面积公式 
 其中
其中  表示球的半径
表示球的半径
假如事件  相互独立,那幺 球的体积公式
相互独立,那幺 球的体积公式 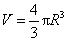
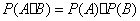 其中
其中  表示球的半径
表示球的半径
假如事件  在一次试验中发生的概率是
在一次试验中发生的概率是  ,
,
那幺 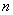 次独立重复试验中恰好发生
次独立重复试验中恰好发生 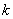 次的概率
次的概率
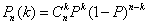
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 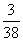 = ( )
= ( )
A.  B.
B.  C.
C. 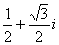 D.
D. 
2. 若 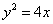 ,且
,且  ,则
,则 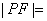 =( )
=( )
A. 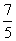 B.
B. 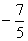 C.
C. 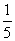 D.-
D.- 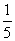
3. 已知 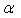 、
、 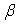 是不同的两个平面,直线
是不同的两个平面,直线 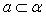 ,直线
,直线 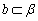 ,命题
,命题  :a与b没有公共点;命题
:a与b没有公共点;命题 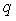 :
:  ,则
,则 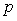 是
是 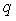 的( )
的( )
A.充分不必要的条件 B.必要不充分的条件
C.充要条件 D.既不充分也不必要的条件
4. 若 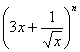 的展开式中各项系数之和为1024,则展开式中含x的整数次幂的项共有 ( )
的展开式中各项系数之和为1024,则展开式中含x的整数次幂的项共有 ( )
A.2项 B.3项 C.5项 D.6项
5. 函数 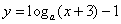
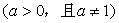 的图象恒过定点
的图象恒过定点  ,若点
,若点  在直线
在直线 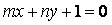 上,其中
上,其中 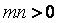 ,则
,则 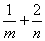 的最小值为( )
的最小值为( )
A.2 B.4 C.8 D.16
6. 等比数列{an}的首项a1=-1,前n项和为Sn,若 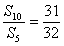 ,则
,则 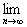 Sn等于 ( )
Sn等于 ( )
 C
C  2 D 2 D  -2 -2
7. 从1,2,3,…,20这20个数中任取2个不同的数,则这两个数之和是3的倍数的概率为 ( )
A. 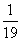 B.
B. 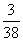 C.
C. 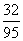 D.
D. 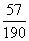
8. 正三棱锥S—ABC中,M是SC的中点, 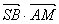 =0,若侧棱
=0,若侧棱  ,则此正三棱锥S—ABC外接球的表面积是
,则此正三棱锥S—ABC外接球的表面积是
A.36π B.64π C.144π D.256π
9. 已知双曲线 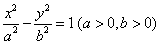 的离心率为
的离心率为 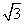 ,若它的一条准线与抛物线
,若它的一条准线与抛物线 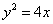 的准线重合。设双曲线与抛物线的一个交点为
的准线重合。设双曲线与抛物线的一个交点为  ,抛物线的焦点为
,抛物线的焦点为 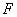 ,则
,则 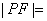
 .
. 
 .
. 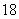
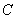 .
. 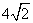
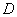 .
. 
10.已知函数 
 上的最小值为-2,则
上的最小值为-2,则 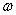 的取值范围是( )
的取值范围是( )
A. 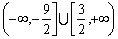 B.
B. 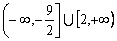 C.
C. 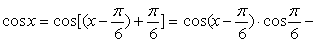 D.
D. 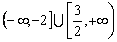
11. 已知f(x)= x 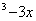 ,过点A(1,m)(m≠-2)可作曲线y=f(x)的三条切线,则m的取值范围是( )
,过点A(1,m)(m≠-2)可作曲线y=f(x)的三条切线,则m的取值范围是( )
A. (-1,1) B. (-2,3) (C) (-1,-2) (D) (-3,-2)
12. 对于函数 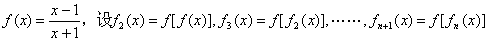
 ,令集合
,令集合 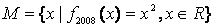 ,则集合M为( )
,则集合M为( )
A.空集 B.实数集 C.单元素集 D.二元素集
二、填空题:本大题共4小题,每小题4分,共16分.请把答案填在答题卡上.
13. 设函数 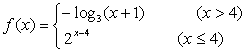 的反函数为
的反函数为 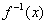 ,且
,且 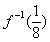 =a,则
=a,则 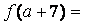 __________
__________
14. 设x,y满足 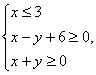 则该不等式组表示的平面区域 ,则z=2x y的最大值是_____________.
则该不等式组表示的平面区域 ,则z=2x y的最大值是_____________.
15. 两个三口之家,拟乘两艘小游艇一起水上游,每艘游艇最多只能坐4个人,其中两个小孩(另4个为两对夫妇)不能独坐一艘游艇,则不同的乘坐方法共有__________.
 16. 如图,矩形ABCD中,DC= 16. 如图,矩形ABCD中,DC= 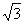 ,AD=1,在DC上截取DE=1,将△ADE沿AE翻折到D1点,点D1在平面ABC上的射影落在AC上时,二面角D1—AE—B的平面角的余弦值是 .
,AD=1,在DC上截取DE=1,将△ADE沿AE翻折到D1点,点D1在平面ABC上的射影落在AC上时,二面角D1—AE—B的平面角的余弦值是 .
三、解答题(本大题共6个小题,共74分,解答应写出文字说明,证实过程或演算步骤)
17.(本小题满分12分)已知 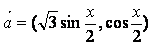 ,
, 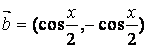 ,函数
,函数 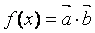 .
.
(1)求 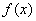 的单调递增区间; (2)若
的单调递增区间; (2)若  ,
,  =
= 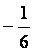 ,求
,求  的值.
的值.
18.(本小题满分12分)某工厂组织工人参加上岗测试,每位测试者最多有三次机会,一旦某次测试通过,便可上岗工作,不再参加以后的测试;否则就一直测试到第三次为止。设每位工人每次测试通过的概率依次为0.2,0.5,0.5.
(1)若有4位工人参加这次测试,求恰有2人通过测试的概率;
(2) 求工人甲在这次上岗测试中参加考试次数 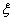 的分布列及E 的分布列及E 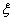 . .

19.(本小题满分12分)如图,直三棱柱A1B1C1—ABC中,C1C=CB=CA=2,AC⊥CB. D、E分别为棱C1C、B1C1的中点.
(1)求 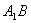 与平面A1C1CA所成角的大小;
与平面A1C1CA所成角的大小;
(2)求二面角B—A1D—A的大小;
(3)在线段AC上是否存在一点F,使得EF⊥平面A1BD?若存在,确定其位置并证实结论;若不存在,说明理由.
20.(本小题满分12分)已知函数f (x) =lnx,g(x) = 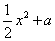 ,(a为常数),若直线l与y =f(x), y =g(x)的图象都相切,且l与y = f(x)的图象相切的切点的横坐标为1.
,(a为常数),若直线l与y =f(x), y =g(x)的图象都相切,且l与y = f(x)的图象相切的切点的横坐标为1.
(1)求直线l的方程及a的值;
(2) 当 –2 ≤m <  时,求h(x)= f(x)—f
时,求h(x)= f(x)—f  (x)[2g(x)- m 1]在[
(x)[2g(x)- m 1]在[ 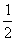 ,2]上的最大值.
,2]上的最大值.
21.(本小题满分12分)已知F1、F2是椭圆  的两个焦点,O为坐标原点,点P
的两个焦点,O为坐标原点,点P 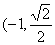 )在椭圆上,线段PF2与y轴的交点M满足
)在椭圆上,线段PF2与y轴的交点M满足  ;⊙O是以F1F2为直径的圆,一直线l: y=kx m与⊙O相切,并与椭圆交于不同的两点A、B.
;⊙O是以F1F2为直径的圆,一直线l: y=kx m与⊙O相切,并与椭圆交于不同的两点A、B.
(1)求椭圆的标准方程;
(2)当 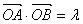 ,且满足
,且满足 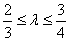 时,求△AOB面积S的取值范围.
时,求△AOB面积S的取值范围.
22.(本小题满分14分) 已知数列 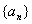 满足
满足 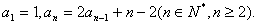
(1) 求数列 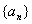 的通项公式;
的通项公式;
(2) 设b 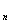 =
=  (n∈N
(n∈N  ,n≥2), b
,n≥2), b 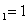 ,
,
①求证:b  b
b 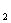 …… b
…… b 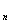 < 3 ;
< 3 ;
②设点M 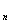 (n,b
(n,b 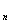 )((n∈N
)((n∈N  ,n>2)在这些点中是否存在两个不同的点同时在函数
,n>2)在这些点中是否存在两个不同的点同时在函数
y = 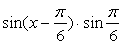 (k>0)的图象上,假如存在,求出点的坐标,若不存在,请说明理由.
(k>0)的图象上,假如存在,求出点的坐标,若不存在,请说明理由.
参考答案
一、选择题 (1)B (2) B (3) B (4) B (5) C(6)B (7)C (8)C(9) D(10) C(11) D(12) A
二、填空题 (13)-2 (14) 15 (15) 48 (16) 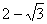
三、解答题
17.解:(1)
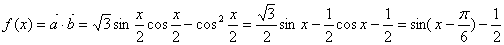 ……4分
……4分
由 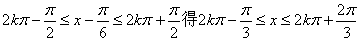

所以 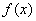 的单调递增区间为
的单调递增区间为 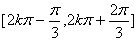
 ………6分
………6分
(2)由 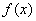 =
=  得:
得: 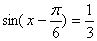

∴  ………8分
………8分
∴ 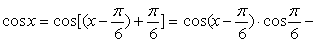
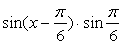
=  …………12分
…………12分
18.解:(1)每位工人通过测试的概率为  .…………2分
.…………2分
每位工人不能通过测试的概率为 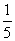 . …………4分
. …………4分
4位工人中恰有2人通过测试的概率为P = C  (
( 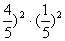 =
= 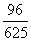 。…………6分
。…………6分
(2) 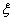 的取值为1、2、3.
的取值为1、2、3.
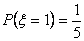 ,
, 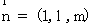 ,
,  .…………8分
.…………8分
故工人甲在这次上岗测试参加考试次数 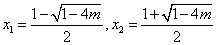 的分布列
的分布列 |
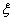
|
1 |
2 |
3 | |

|
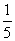
|
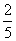
|
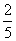
| |