|
一、选择题:本题共12小题,每小题5分,共60分,在每小题给出的四个备选项中,只有一项是符合题目要求的.
若 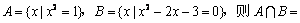 \* MERGEFORMAT
( )
\* MERGEFORMAT
( )
A.{3} B.{1} C. 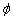 \* MERGEFORMAT
D.{– 1}
\* MERGEFORMAT
D.{– 1}
若 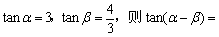 \* MERGEFORMAT
( )
\* MERGEFORMAT
( )
A.– 3 B. 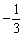 \* MERGEFORMAT
C.3 D.
\* MERGEFORMAT
C.3 D. 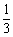 \* MERGEFORMAT
\* MERGEFORMAT
函数 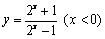 \* MERGEFORMAT
的反函数是( )
\* MERGEFORMAT
的反函数是( )
A. 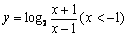 \* MERGEFORMAT
B.
\* MERGEFORMAT
B.  \* MERGEFORMAT
\* MERGEFORMAT
C. 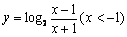 \* MERGEFORMAT
D.
\* MERGEFORMAT
D. 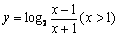 \* MERGEFORMAT
\* MERGEFORMAT
不等式 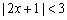 \* MERGEFORMAT
的解集是( )
\* MERGEFORMAT
的解集是( )
A. 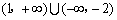 \* MERGEFORMAT
B.(– 1,2)
\* MERGEFORMAT
B.(– 1,2)
C.  \* MERGEFORMAT
D.(– 2,1)
\* MERGEFORMAT
D.(– 2,1)
椭圆 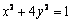 \* MERGEFORMAT
的离心率为( )
\* MERGEFORMAT
的离心率为( )
A.  \* MERGEFORMAT
B.
\* MERGEFORMAT
B. 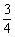 \* MERGEFORMAT
C.
\* MERGEFORMAT
C. 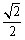 \* MERGEFORMAT
D.
\* MERGEFORMAT
D.  \* MERGEFORMAT
\* MERGEFORMAT
已知 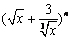 \* MERGEFORMAT
展开式中,各项系数的和与其各项二项式系数的和之比为64,则n等于( )
\* MERGEFORMAT
展开式中,各项系数的和与其各项二项式系数的和之比为64,则n等于( )
A.4 B.5 C.6 D.7
 为了了解某校学生的身体发育情况,抽查了该校100名高中男生的体重情况,根据所得数据画出样本的频率分布直方图如图所示,根据此图,估计该校2000名高中男生中体重大于70.5公斤的人数为( ) 为了了解某校学生的身体发育情况,抽查了该校100名高中男生的体重情况,根据所得数据画出样本的频率分布直方图如图所示,根据此图,估计该校2000名高中男生中体重大于70.5公斤的人数为( )
A.400 B.200 C.128 D.20
连掷两次骰子得到的点数分别为m和n,记向量a = (m,n)与向量b = (1,– 1)的夹角为  \* MERGEFORMAT
,则
\* MERGEFORMAT
,则  \* MERGEFORMAT
的概率是( )
\* MERGEFORMAT
的概率是( )
A.  \* MERGEFORMAT
B.
\* MERGEFORMAT
B. 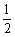 \* MERGEFORMAT
C.
\* MERGEFORMAT
C. 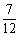 \* MERGEFORMAT
D.
\* MERGEFORMAT
D. 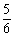 \* MERGEFORMAT
\* MERGEFORMAT
“a = b”是“直线y = x 2与圆 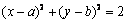 \* MERGEFORMAT
相切”的( )
\* MERGEFORMAT
相切”的( )
A.必要不充分条件 B.充分不必要条件
C.充分必要条件 D.既不充分也不必要条件
把函数  \* MERGEFORMAT
的图象按向量
\* MERGEFORMAT
的图象按向量  \* MERGEFORMAT
平移后,得到
\* MERGEFORMAT
平移后,得到  \* MERGEFORMAT
的图象,则
\* MERGEFORMAT
的图象,则 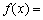 \* MERGEFORMAT
( )
\* MERGEFORMAT
( )
A. 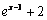 \* MERGEFORMAT
B.
\* MERGEFORMAT
B. 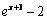 \* MERGEFORMAT
C.
\* MERGEFORMAT
C.  \* MERGEFORMAT
D.
\* MERGEFORMAT
D. 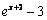 \* MERGEFORMAT
\* MERGEFORMAT
下列正方体或正四面体中,P、Q、R、S分别是所在棱的中点,这四个点不共面的一个图是( )
 \* MERGEFORMAT
\* MERGEFORMAT
A B C D
设集合M = {1,2,3,4,5,6},S1、S2、…、Sk都是M的含两个元素的子集,且满足:对任意的 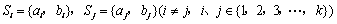 \* MERGEFORMAT
,都有
\* MERGEFORMAT
,都有  \* MERGEFORMAT
\* MERGEFORMAT
 \* MERGEFORMAT
.则k的最大值是( )
\* MERGEFORMAT
.则k的最大值是( )
A.10 B.11 C.12 D.13
二、填空题:本题共4小题,每小题4分,共16分,把答案填写在答题卡相应位置上.
设变量x、y满足约束条件 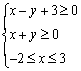 \* MERGEFORMAT
,则目标函数
\* MERGEFORMAT
,则目标函数 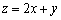 \* MERGEFORMAT
的最小值为____________.
\* MERGEFORMAT
的最小值为____________.
已知函数  \* MERGEFORMAT
为偶函数,它的最小正周期是3,
\* MERGEFORMAT
为偶函数,它的最小正周期是3, 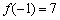 \* MERGEFORMAT
,则
\* MERGEFORMAT
,则  \* MERGEFORMAT
____________.
\* MERGEFORMAT
____________.
在正方体上任意选择4个顶点,它们可能是如下各种几何形体的4个顶点,这些几何形体是______________.(写出所有正确的结论的编号)
①矩形;②不是矩形的平行四边形;③有三个面为等腰直角三角形,另一个面为等边三角形的四面体;④每个面都是等边三角形的四面体;⑤每个面都是直角三角形的四面体.
16. 对于一切实数x,令 [ x ] 为不大于x的最大整数,则函数  \* MERGEFORMAT
为高斯实数或取实数,若
\* MERGEFORMAT
为高斯实数或取实数,若  \* MERGEFORMAT
,Sn为数列{an}的前几项和,则
\* MERGEFORMAT
,Sn为数列{an}的前几项和,则  \* MERGEFORMAT
____________.
\* MERGEFORMAT
____________.
三、解答题:本题共6小题,共74分,解答时应写出必要的文字说明、证实过程及演算步骤.
17.(本小题满分13分)
已知向量 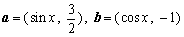 \* MERGEFORMAT
\* MERGEFORMAT
当a // b时,求  \* MERGEFORMAT
的值;
\* MERGEFORMAT
的值;
求 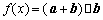 \* MERGEFORMAT
的值域.
\* MERGEFORMAT
的值域.
18.(本小题满分13分)
一次考试中共12道选择题,每道题都有4个选项,其中有且只有一个选项是正确答案:每题答对得5分,不答或答错得0分.某考生已确定有8道题的答案是正确的,其余题中:有两道题可以判定两个选项是错误的,有一道题可以判定一个选项是错误的,还有一道因不理解题意只好乱猜.求出该考生:
得60分的概率;
恰有一道错误的概率.
19.(本小题满分12分)
已知实数列{an}是等比数列,其中a7 = 1,且a4,a5 1,a6成等差数列.
求数列{an}的通项公式;
数列{an}的前n项和记为Sn,证实:  \* MERGEFORMAT
.
\* MERGEFORMAT
.
20.(本小题满分12分)
如图,在Rt△AOB中,  \* MERGEFORMAT
,斜边AB = 4,Rt△AOC可以通过Rt△AOB以直线AO为轴旋转而得,且二面角B—AO—C是直二面角,动点D在斜边AB上.
\* MERGEFORMAT
,斜边AB = 4,Rt△AOC可以通过Rt△AOB以直线AO为轴旋转而得,且二面角B—AO—C是直二面角,动点D在斜边AB上.
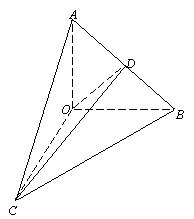 求证:平面COD⊥平面AOB; 求证:平面COD⊥平面AOB;
当D在AB中点时,求异面线AO与CD所成角的大小;
求CD与平面AOB所成角的最大值.
21.(本小题满分12分)
设函数 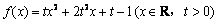 \* MERGEFORMAT
.
\* MERGEFORMAT
.
求 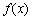 \* MERGEFORMAT
的最小值
\* MERGEFORMAT
的最小值 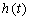 \* MERGEFORMAT
;
\* MERGEFORMAT
;
若  \* MERGEFORMAT
对
\* MERGEFORMAT
对 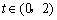 \* MERGEFORMAT
恒成立,求实数m的取值范围.
\* MERGEFORMAT
恒成立,求实数m的取值范围.
22.(本小题满分12分)
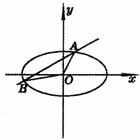 如图,直线 如图,直线  \* MERGEFORMAT
与椭圆
\* MERGEFORMAT
与椭圆  \* MERGEFORMAT
交于A、B两点,记△AOB的面积为S.
\* MERGEFORMAT
交于A、B两点,记△AOB的面积为S.
求在k = 0,0 < b < 1的条件下,S的最大值;
当 | AB | = 2,S = 1时,求直线AB的方程.
数学试题参考答案(文科)
2008年3月
一、选择题:本题共12小题,每小题5分,共60分,在每小题给出的四个备选项中,只有一项是符合题目要求的.
1.D 2.D 3.A 4.D 5.A 6.C 7.A 8.C 9.B 10.C 11.D 12.B
二、填空题:本题共4小题,每小题4分,共16分.
13.  \* MERGEFORMAT
14.7 15.①③④⑤ 16.
\* MERGEFORMAT
14.7 15.①③④⑤ 16.  \* MERGEFORMAT
\* MERGEFORMAT
三、解答题:本题共6小题,共74分.
17.解:(1) 由  \* MERGEFORMAT
得
\* MERGEFORMAT
得
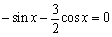 \* MERGEFORMAT
\* MERGEFORMAT
∴  \* MERGEFORMAT
\* MERGEFORMAT
∴ 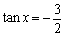 \* MERGEFORMAT
\* MERGEFORMAT
又 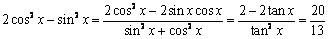 \* MERGEFORMAT
\* MERGEFORMAT
(2) 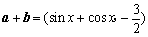 \* MERGEFORMAT
\* MERGEFORMAT
∴ 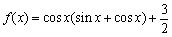 \* MERGEFORMAT
\* MERGEFORMAT
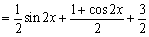 \* MERGEFORMAT
\* MERGEFORMAT
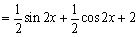 \* MERGEFORMAT
\* MERGEFORMAT
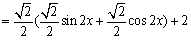 \* MERGEFORMAT
\* MERGEFORMAT
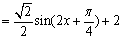 \* MERGEFORMAT
\* MERGEFORMAT
∴ 值域为 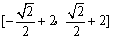 \* MERGEFORMAT
\* MERGEFORMAT
18.解:(1)  \* MERGEFORMAT
\* MERGEFORMAT
(2) 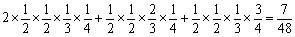 \* MERGEFORMAT
\* MERGEFORMAT
19.解:(1) 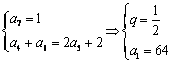 \* MERGEFORMAT
\* MERGEFORMAT
∴ 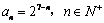 \* MERGEFORMAT
\* MERGEFORMAT
(2)  \* MERGEFORMAT
\* MERGEFORMAT
|
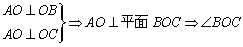 \* MERGEFORMAT
即为二面角B—AO—C
\* MERGEFORMAT
即为二面角B—AO—C
| | 20.(1) 证实:
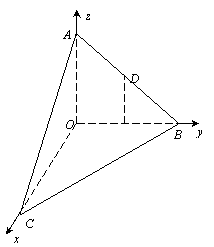  \* MERGEFORMAT
\* MERGEFORMAT
(2) 解:建立以O为坐标原点的空间直角坐标系
O(0,0,0),A(0,0, 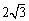 \* MERGEFORMAT
),
\* MERGEFORMAT
),
C(2,0,0),D(0,1,  \* MERGEFORMAT
)
\* MERGEFORMAT
)
∴ 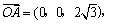 \* MERGEFORMAT
\* MERGEFORMAT
 \* MERGEFORMAT
\* MERGEFORMAT
∴ 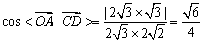 \* MERGEFORMAT
\* MERGEFORMAT
∴ 所成角的大小为  \* MERGEFORMAT
\* MERGEFORMAT
(3) OC⊥平面AOB
∴ 平面AOB的法向量为 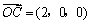 \* MERGEFORMAT
\* MERGEFORMAT
D (0,y, 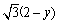 \* MERGEFORMAT
)
\* MERGEFORMAT
)
∴  \* MERGEFORMAT
,即求
\* MERGEFORMAT
,即求 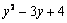 \* MERGEFORMAT
的最小值
\* MERGEFORMAT
的最小值
∴  \* MERGEFORMAT
\* MERGEFORMAT
 \* MERGEFORMAT
即求
\* MERGEFORMAT
即求 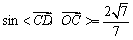 \* MERGEFORMAT
\* MERGEFORMAT
21.解:(1) 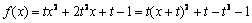 \* MERGEFORMAT
\* MERGEFORMAT
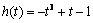 \* MERGEFORMAT
\* MERGEFORMAT
(2) 即 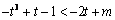 \* MERGEFORMAT
对
\* MERGEFORMAT
对 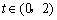 \* MERGEFORMAT
恒成立
\* MERGEFORMAT
恒成立
又即 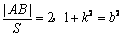 \* MERGEFORMAT
对
\* MERGEFORMAT
对 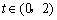 \* MERGEFORMAT
恒成立
\* MERGEFORMAT
恒成立
令 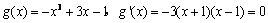 \* MERGEFORMAT
\* MERGEFORMAT
 \* MERGEFORMAT
在(0,1)递增,在(1,2)递减
\* MERGEFORMAT
在(0,1)递增,在(1,2)递减
∴在(0,2)内有最大值 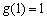 \* MERGEFORMAT
,从而m > 1
\* MERGEFORMAT
,从而m > 1
22.解:(1) 当k = 0时, 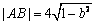 \* MERGEFORMAT
\* MERGEFORMAT
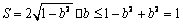 \* MERGEFORMAT
(当
\* MERGEFORMAT
(当  \* MERGEFORMAT
时取“=”)
\* MERGEFORMAT
时取“=”)
∴ S的最大值为1
(2) 由(1)可知, 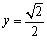 \* MERGEFORMAT
不满足条件
\* MERGEFORMAT
不满足条件
设 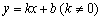 \* MERGEFORMAT
①
\* MERGEFORMAT
①
①与  \* MERGEFORMAT
联立得:
\* MERGEFORMAT
联立得:  \* MERGEFORMAT
\* MERGEFORMAT
 \* MERGEFORMAT
①
\* MERGEFORMAT
①
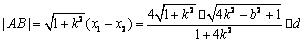 \* MERGEFORMAT
\* MERGEFORMAT
∴  \* MERGEFORMAT
\* MERGEFORMAT
由 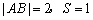 \* MERGEFORMAT
可知,
\* MERGEFORMAT
可知, 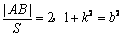 \* MERGEFORMAT
,
\* MERGEFORMAT
, 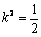 \* MERGEFORMAT
,
\* MERGEFORMAT
, 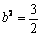 \* MERGEFORMAT
,此时代入①
\* MERGEFORMAT
,此时代入①  \* MERGEFORMAT
\* MERGEFORMAT
∴ 直线AB的方程为: 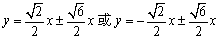 \* MERGEFORMAT
\* MERGEFORMAT
|