|
高考文科数学一模考试试题
参考公式:
假如事件 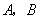 互斥,那么 球的表面积公式
互斥,那么 球的表面积公式 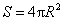
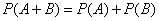 其中
其中 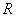 表示球的半径
表示球的半径
假如事件 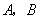 相互独立,那么 球的体积公式
相互独立,那么 球的体积公式 
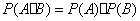 其中
其中 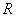 表示球的半径
表示球的半径
假如事件 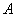 在一次试验中发生的概率是
在一次试验中发生的概率是 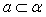 ,
,
那么 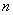 次独立重复试验中恰好发生
次独立重复试验中恰好发生 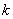 次的概率
次的概率
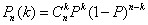
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知集合 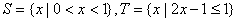 则S∩T等于
则S∩T等于
A.S B.T C. 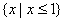 D.φ
D.φ
2. 函数 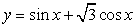 的周期为
的周期为
A. 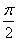 B.
B. 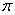 C.
C. 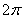 D.
D. 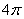
3. 已知 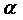 、
、 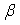 是不同的两个平面,直线
是不同的两个平面,直线 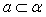 ,直线
,直线  ,命题
,命题 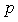 :
: 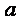 与
与  没有公共点;命题
没有公共点;命题 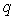 :
: 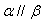 ,则
,则  是
是 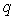 的
的
A.充分不必要的条件 B.必要不充分的条件
C.充要条件 D.既不充分也不必要的条件
4. 若 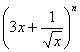 的展开式中各项系数之和为1024,则展开式中含x的整数次幂的项共有
的展开式中各项系数之和为1024,则展开式中含x的整数次幂的项共有
A.2项 B.3项 C.5项 D.6项
5. 函数 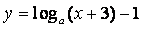
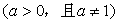 的图象恒过定点
的图象恒过定点 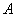 ,若点
,若点 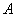 在直线
在直线 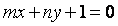 上,其中
上,其中 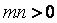 ,则
,则 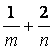 的最小值为
的最小值为
A.2 B.4 C.8 D.16
6. 已知等差数列  中,
中, 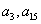 是方程
是方程 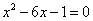 的两根,则
的两根,则 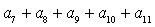 等于
等于
A. 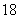 B.
B. 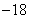 C.
C. 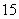 D.
D. 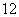
7. 先后连掷两次骰子分别得到点数m、n,则向量(m,n)与向量(-1,1)的夹角 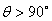 的概率是
的概率是
A. 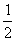 B.
B. 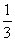 C.
C. 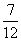 D.
D. 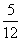
8. 正三棱锥S—ABC中,若侧棱 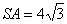 ,高SO =4,则此正三棱锥S—ABC外接球的表面积是
,高SO =4,则此正三棱锥S—ABC外接球的表面积是
A.36π B.64π C.144π D.256π
9. 已知双曲线 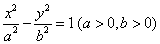 的离心率为
的离心率为 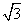 ,若它的一条准线与抛物线
,若它的一条准线与抛物线 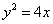 的准线重合。设双曲线与抛物线的一个交点为
的准线重合。设双曲线与抛物线的一个交点为 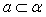 ,抛物线的焦点为
,抛物线的焦点为 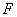 ,则
,则 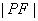 等于
等于
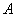 .
. 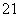
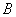 .
. 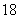
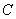 .
. 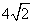
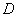 .
. 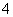
10. 已知函数 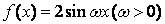 在区间
在区间 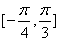 上的最小值是
上的最小值是 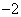 则
则 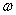 的最小值等于A.
的最小值等于A. 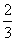 B.
B. 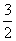 C.2 D.3
C.2 D.3
11. 己知函数f(x)= 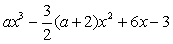 ,若方程f(x)=0有三个不同的解,则a的取值范围是
,若方程f(x)=0有三个不同的解,则a的取值范围是
A. [2, ∞ 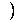 B.(-∞,2
B.(-∞,2 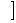 C. (0,2) D. (-∞,0)
C. (0,2) D. (-∞,0)
12. 假如数列  满足,
满足, 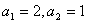 且
且 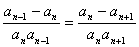 (
( 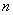 ≥2),则此数列的第12项为
≥2),则此数列的第12项为
A.  B.
B. 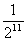 C.
C. 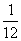 D.
D. 
二、填空题:本大题共4小题,每小题4分,共16分.请把答案填在答题卡上.
13. 函数 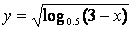 的定义域是_________.
的定义域是_________.
14. 设x,y满足 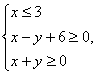 则该不等式组表示的平面区域 ,则z=2x y的最大值_________.
则该不等式组表示的平面区域 ,则z=2x y的最大值_________.
15. 两个三口之家,拟乘两艘小游艇一起水上游,每艘游艇最多只能坐4个人,其中两个小孩(另4个为两对夫妇)不能独坐一艘游艇,则不同的乘坐方法共有__________.
16. 在△ABC中,AB =3,AC =5,∠BAC =120°,其所在平面外一点P到A、B、C三个顶点的距离都是14,则P点到直线BC的距离为 .
三、解答题(本大题共6个小题,共74分,解答应写出文字说明,证实过程或演算步骤)
17.(本小题满分12分)已知 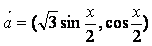 ,
, 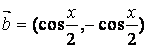 ,函数
,函数 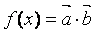 .
.
(1)求 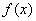 的单调递增区间; (2)若
的单调递增区间; (2)若 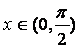 ,
, 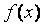 =
= 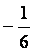 ,求
,求 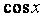 的值.
的值.
18.(本小题满分12分)某工厂组织工人参加上岗测试,每位测试者最多有三次机会,一旦某次测试通过,便可上岗工作,不再参加以后的测试;否则就一直测试到第三次为止。设每位工人每次测试通过的概率依次为0.2,0.4,0.5。
(1) 若有3位工人参加这次测试,求至少有一人不能上岗的概率。
(2) 若有4位工人参加这次测试,求恰有2人通过测试的概率。
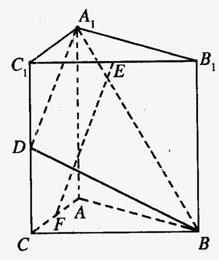
19.(本小题满分12分)如图,直三棱柱A1B1C1—ABC中,C1C=CB=CA=2,AC⊥CB. D、E分别为棱C1C、B1C1的中点.
(1)求 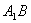 与平面A1C1CA所成角的大小;
与平面A1C1CA所成角的大小;
(2)求二面角B—A1D—A的大小;
(3)在线段AC上是否存在一点F,使得EF⊥平面A1BD?若存在,确定其位置并证实结论;若不存在,说明理由.
20.(本小题满分12分)已知曲线C: 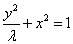 .
.
(1)由曲线C上任一点E向 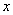 轴作垂线,垂足为F,点P分
轴作垂线,垂足为F,点P分 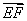 所成的比为
所成的比为 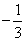 ,求点P的轨迹. P的轨迹可能是圆吗?请说明理由;
,求点P的轨迹. P的轨迹可能是圆吗?请说明理由;
(2)假如直线l的斜率为 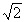 ,且过点M(0,
,且过点M(0, 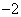 ),直线l交曲线C于A、B两点,又
),直线l交曲线C于A、B两点,又 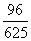 ,求曲线C的方程.
,求曲线C的方程.
21.(本小题满分12分) 已知:函数 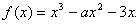
(1)若 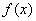 在
在 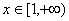 上是增函数,求实数a的取值范围;
上是增函数,求实数a的取值范围;
(2)若方程f(x)=( 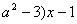 (a>0)至多有两个解,求实数a的取值范围.
(a>0)至多有两个解,求实数a的取值范围.
22.(本小题满分14分)数列  的各项均为正数,
的各项均为正数, 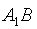 为其前
为其前 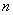 项和,对于任意
项和,对于任意 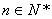 ,总有
,总有 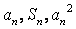 成等差数列.
成等差数列.
(1)求数列  的通项公式;
的通项公式;
(2)若b 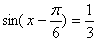 =a
=a 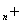 4
4 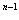 (
( 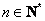 ), B
), B 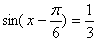 是数列{b
是数列{b 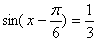 }的前
}的前 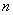 项和,
项和,
求证:不等式 B  ≤4B
≤4B 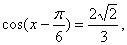 ,对任意
,对任意 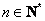 皆成立.
皆成立.
(3)令 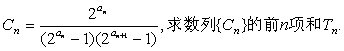
参考答案
一、选择题(1)A (2) C (3) B (4) B (5) C(6)C (7)D (8)C(9) D(10) C(11)D(12) D
二、填空题(13) 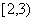 (14) 15 (15) 48 (16)
(14) 15 (15) 48 (16) 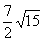
三、解答题
17. 解:(1)
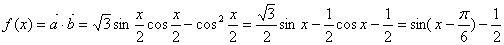 ……4分
……4分
由 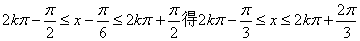
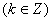
所以 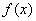 的单调递增区间为
的单调递增区间为 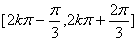
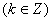 ………6分
………6分
(2)由 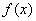 =
= 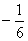 得:
得: 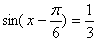
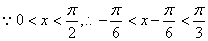
∴ 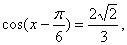 ………8分
………8分
∴ 
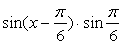
= 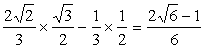 …………12分
…………12分
18. 解:1) 每位工人通过测试的概率为 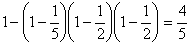 …………2分
…………2分
每位工人不能通过测试的概率为 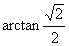 .…………4分
.…………4分
3人中至少有一人不能通过测试的概率 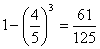 .…………6分
.…………6分
(2) 4位工人中恰有2人通过测试的概率为P=C 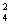 (
( 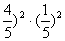 =
= 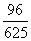 …………12分 。
…………12分 。
19. 解:(1)∵A1B1C1-ABC为直三棱柱 ∴CC1⊥底面ABC ∴CC1⊥BC
∵AC⊥CB ∴BC⊥平面A1C1CA ………………2分
∴ 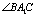 为
为 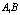 与平面A1C1CA所成角
与平面A1C1CA所成角 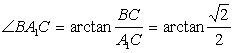
∴ 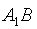 与平面A1C1CA所成角为
与平面A1C1CA所成角为 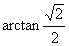 ……………4分
……………4分
(2)分别延长AC,A1D交于G. 过C作CM⊥A1G 于M,连结BM
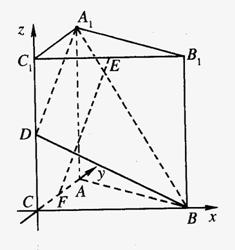 ∵BC⊥平面ACC1A1 ∴CM为BM在平面A1C1CA的内射影 ∵BC⊥平面ACC1A1 ∴CM为BM在平面A1C1CA的内射影
∴BM⊥A1G ∴∠CMB为二面角B—A1D—A的平面角……6分
平面A1C1CA中,C1C=CA=2,D为C1C的中点
∴CG=2,DC=1 在直角三角形CDG中,
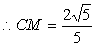
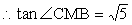 ,
,
即二面角B—A1D—A的大小为  …………………8分
…………………8分
(3)在线段AC上存在一点F,使得EF⊥平面A1BD………10分
其位置为AC中点,证实如下:
∵A1B1C1—ABC为直三棱柱 , ∴B1C1//BC
∵由(1)BC⊥平面A1C1CA,∴B1C1⊥平面A1C1CA
∵EF在平面A1C1CA内的射影为C1F ,F为AC中点 ∴C1F⊥A1D ∴EF⊥A1D ……11分
同理可证EF⊥BD, ∴EF⊥平面A1BD …………12分
∵E为定点,平面A1BD为定平面 ,点F唯一
解法二:(1)同解法一……………………4分
(2)∵A1B1C1—ABC为直三棱住 C1C=CB=CA=2 , AC⊥CB D、E分别为C1C、B1C1的中点, 建立如图所示的坐标系得
C(0,0,0) B(2,0,0) A(0,2,0)
C1(0,0,2) B1(2,0,2) A1(0,2,2)
D(0,0,1) E(1,0,2)………………6分
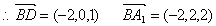 设平面A1BD的法向量为
设平面A1BD的法向量为 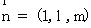
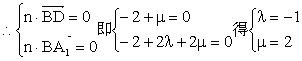
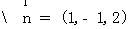 ……………8分
……………8分
平面ACC1A1的法向量为 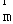 =(1,0,0)
=(1,0,0) 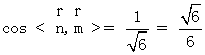 …9分
…9分
即二面角B—A1D—A的大小为 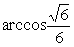 ……………10分
……………10分
(3)在线段AC上存在一点F,设F(0,y,0)使得EF⊥平面A1BD
欲使EF⊥平面A1BD 由(2)知,当且仅当 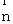 //
// 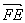 …………11分
…………11分
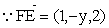
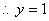 … ……13分
… ……13分
∴存在唯一一点F(0,1,0)满足条件. 即点F为AC中点……12分
20.解:(1)设 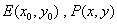 ,则
,则 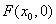 ,
,
∵点P分 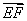 所成的比为
所成的比为 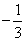 ∴
∴ 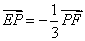
∴ 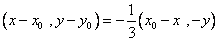
∴ 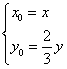
代入 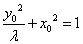 中,得
中,得 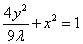 为P点的轨迹方程.
为P点的轨迹方程.
当 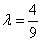 时,轨迹是圆。 ……6分
时,轨迹是圆。 ……6分
(2)由题设知直线l的方程为 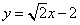 , 设
, 设 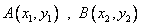
联立方程组 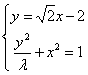 ,消去
,消去 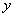 得:
得: 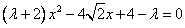 .
.
∵ 方程组有两解 ∴ 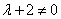 且
且 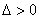 ∴
∴  或
或 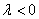 且
且 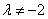 …………8分
…………8分
又已知 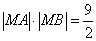 ,M、A、B三点共线,由向量知识得
,M、A、B三点共线,由向量知识得 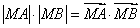 或
或
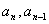 ,而
,而
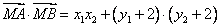
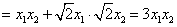 ∴
∴ 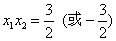
又 ∵ 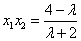 ∴
∴ 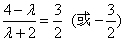 解得
解得 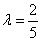 (舍去)或
(舍去)或 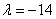
∴ 曲线C的方程是  . ……………12分
. ……………12分
(21)解析:(1) 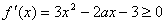 ………2分
………2分 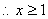
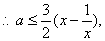
当x≥1时, 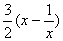 是增函数,其最小值为
是增函数,其最小值为 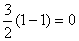
 ………6分
………6分
(2) 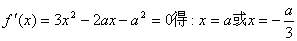

|
x |
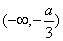
|
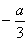
|
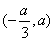
|
a |
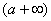
| |

|
|
0 |
- |
0 |
| |
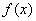
|

|
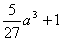
|

|
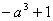
|

| |