| |
|
[组图]高考理科数学杭州市第一次教学质量检测
|
| 查询数高考考试的详细结果
|
|
高考理科数学杭州市第一次教学质量检测
试题卷()
考生须知:
1. 本卷满分150分, 考试时间120分钟.
2. 答题前, 在答题卷密封区内填写学校、班级和姓名.
3. 所有答案必须写在答题卷上, 写在试题卷上无效.
4. 考试结束, 只需上交答题卷.
参考公式
假如事件  互斥,那么
互斥,那么 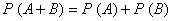 ;
;
假如事件  相互独立,那么
相互独立,那么 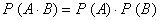 ;
;
假如事件 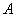 在一次试验中发生的概率是
在一次试验中发生的概率是 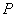 ,那么
,那么 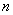 次独立重复试验中事件A恰好发生
次独立重复试验中事件A恰好发生 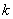 次的概率
次的概率  .
.
一. 选择题 : 本大题共10小题, 每小题5分, 共50分. 在每小题给出的四个选项中, 只有一项是符合题目要求的 .
1. 若集合 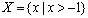 ,则下列关系成立的是( 宗 )
,则下列关系成立的是( 宗 )
(A) 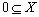 (B)
(B) 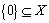 (C)
(C) 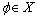 (D)
(D) 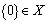
2. 已知复数z = (2 3i)( 1 – 4i ) , 则z在复平面上对应的点Z位于( )
(A) 第一象限 (B) 第二象限 (C) 第三象限 (D) 第四象限
3.数据 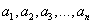 的方差为
的方差为 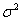 ,则数据
,则数据 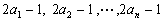 的方差为( )
的方差为( )
(A) 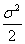 (B)
(B) 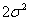 -1 (C) )
-1 (C) )  (D)
(D)  -1
-1
4. 如图,已知单位圆O与y轴相交于A、B两点.角θ的顶点为原点,始边在x轴的正半轴上,终边在射线OC上. 过点A作直线AC垂直于y轴且与角θ的终边交于点C,则有向线段AC的函数值是( )
(A)sinθ (B) cosθ (C) tanθ (D) cotθ
5. 在锐角△ABC中,若lg (1+sinA) = m , 且lg 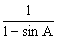 = n,则lgcosA等于( )
= n,则lgcosA等于( )
(A) 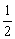 (m-n) (B)m-n (C)
(m-n) (B)m-n (C) 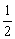 ( m+
( m+ 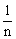 ) (D)m+
) (D)m+ 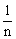
6. 从1到10十个数中,任意选取4个数,其中,第二大的数是7的情况共有 ( )
(A)18 种 (B)30种 (C)45种 (D)84种
7.若 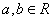 ,使
,使 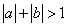 成立的一个充分不必要条件是 ( )
成立的一个充分不必要条件是 ( )
(A) 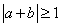 (B)
(B) 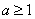 (C)
(C) 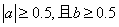 (D)
(D) 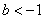
8. 在等差数列 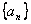 中,
中, 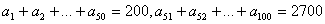 ,
,
则 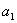 为( )
为( )
(A) 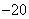 (B)
(B) 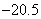 (C)
(C) 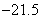 (D)
(D) 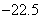
9.已知函数 f ( x) = (x2 – 3x 2) g ( x ) 3x – 4 , 其中g ( x )是定义域为R的连续函数,则方程f ( x) = 0在下面哪个范围内必有实数根 ( )
(A) ( 0, 1 ) (B) (1, 2 ) (C) ( 2 , 3 ) (D) ( 2, 4 )
10. 已知偶函数f (x )满足条件:当x ÎR时,恒有 f ( x 2 ) = f (x ) , 且0 £ x £ 1时,有f ` ( x ) >0,则 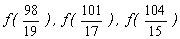 的大小关系是 ( B )
的大小关系是 ( B )
(A) 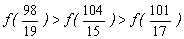 (B)
(B) 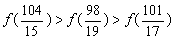
(C) 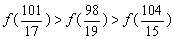 (D)
(D) 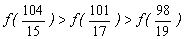
二.填空题: 本大题有 7小题, 每小题4分, 共28分. 把答案填在答题卷的相应位置上.
11. 函数 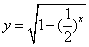 的定义域是_ ____
的定义域是_ ____
12. 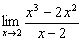 = .
= .
13. 化简 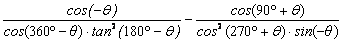 = 。
= 。
14. 二项式 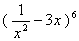 的展开式中, 常数项的值是 .
的展开式中, 常数项的值是 .
15. 函数 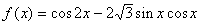 的最小正周期是__________。
的最小正周期是__________。
16. 设实数 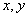 满足
满足 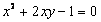 ,则
,则 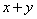 的取值范围是__ __.
的取值范围是__ __.
17. 设向量 a n = 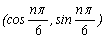 ,向量b的模为
,向量b的模为 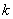 (k为常数),则y = |a 1 b|2 |a 2 b| 2 … |a 10 b| 2的最大值与最小值的差等于. .
(k为常数),则y = |a 1 b|2 |a 2 b| 2 … |a 10 b| 2的最大值与最小值的差等于. .
三. 解答题: 本大题有5小题, 共72分. 解答应写出文字说明, 证实过程或演算步骤.
18. (本小题满分14分)
已知 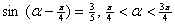 , 求:
, 求:
(1) 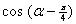 的值; (2)
的值; (2) 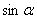 的值;
的值;
(3) 函数 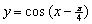 的图象可以通过函数
的图象可以通过函数 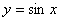 的图象进行怎样的平移得到?
的图象进行怎样的平移得到?
19. (本小题满分14分)
解关于x的不等式 2x – | x – a | > 2
20.(本小题满分14分)
暗箱中开始有3个红球,2个白球.每次从暗箱中取出一球后,将此球以及与它同色的5个球(共六个球)一齐放回暗箱中。
(1) 求第二次取出红球的概率
(2) 求第三次取出白球的概率;
(3) 设取出白球得5分,取出红球得8分,求连续取球3次得分的期望值.
21 . (本小题满分14分)
已知向量x = (1,t2 – 3 ) , y = (–k ,t) (其中实数k和t不同时为零),当| t | £ 2时, 有 x⊥y ,当| t | > 2时,有x∥y.
(1) 求函数关系式k = f (t ) ;
(2) 求函数f (t )的单调递减区间;
(3) 求函数f (t )的最大值和最小值.
22.(本小题满分16分)
已知数列{bn}满足条件: 首项b1 = 1, 前n项之和Bn = 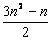 .
.
(1) 求数列{bn}的通项公式 ;
(2) 设数列{an}的满足条件:an= (1+ 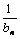 ) a n – 1 ,且a1 = 2 , 试比较an与
) a n – 1 ,且a1 = 2 , 试比较an与 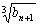 的大小,并证实你的结论.
的大小,并证实你的结论.
数学参考评分标准(理科)
一. 选择题 : (本大题共10小题, 每小题5分, 共50分) |
题号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 | |
答案 |
B |
D |
C |
D |
A |
C |
D |
B |
B |
B | |
二.填空题: 本大题有 7小题, 每小题4分, 共28分. 把答案填在答题卷的相应位置上.
11. [0,¥) 12. 4 .
13. – 1 14. 1215 .
15. p 16. (–¥, – 1]∪[1,¥)
17. 2( 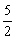 )k .
)k .
三. 解答题: 本大题有5小题, 共72分. 解答应写出文字说明, 证实过程或演算步骤.
18. (本小题满分14分)
(1) ∵ 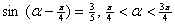 , ∴
, ∴ 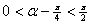 , 有
, 有 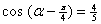 ; --- 4分
; --- 4分
(2) 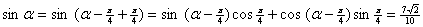 ; --- 5分
; --- 5分
(3) 函数 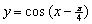 的图象可以通过函数
的图象可以通过函数 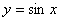 的图象向左平移
的图象向左平移 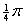 个单位得到. --- 5分
个单位得到. --- 5分
19. (本小题满分14分)
1.当x < a时, 不等式化成: 2x x– a > 2, 得 x > 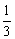 ( a 2), 2分
( a 2), 2分
a = 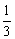 ( a 2), 得a = 1 1分
( a 2), 得a = 1 1分
1) 当 a £ 1时, ∵ 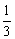 ( a 2) ≥ a , ∴ 无解 ,
( a 2) ≥ a , ∴ 无解 ,
2) 当 a >1时, ∵ 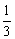 ( a 2) < a, ∴解为
( a 2) < a, ∴解为 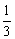 ( a 2)< x < a . 3分
( a 2)< x < a . 3分
2.当x ³ a 时, 不等式化成: 2x –x a > 2, 得 x > 2 – a , 2分
由a =2 – a,得a = 1 1分
1) 当 a £ 1时, ∵a <2 – a , ∴x > 2 – a,
2) 当a > 1时, ∵a >2 – a, ∴ x ³ a. 3分
综合上述: 当 a £ 1时, 原不等式解为 x >2 – a ,
当a >1时, 原不等式解为 x > 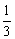 ( a 2) 2分
( a 2) 2分
其它解法: 1 ) 2x – 2 > | x – a | 平方求解.
2) 图象法
对照上面给分.
20.(本小题满分14分)
设第n次取出白球的概率为Pn, 第n次取出红球的概率为Qn,
(1) 第二次取出红球的概率Q2 = 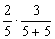
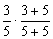 =
= 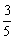 5分(每项2分)
5分(每项2分)
(2) 三次取的过程共有下列情况:
白白白,白红白,红白白,红红白,
第三次取出白球的概率
P3 = 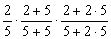
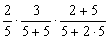
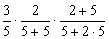
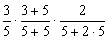
= 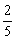 5分(每项1分)
5分(每项1分)
(3) 连续取球3次,得分的情况共有
5 5 5 , 5 8 5, 8 5 5, 8 8 5, 5 5 8 , 5 8 8, 8 5 8,8 8 8
列表如下:
得分期望x = 15´ 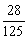 18´
18´ 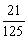 21´
21´ 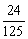 24´
24´ 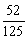 =
= 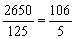 4分
4分
21 . (本小题满分14分)
(1) 当| t | £ 2时,由x⊥y得:x·y = – k (t2 – 3 ) t = 0,
得k = f (t ) = t3 – 3t ( | t | £ 2 )
当| t | > 2时, 由x∥y得: k = 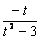
所以k = f (t ) =  5分
5分
(2) 当| t | £ 2时, f `(t ) =3 t2 – 3 , 由f `(t ) < 0 , 得3 t2 – 3 < 0
解得 –1 < t < 1 ,
当| t | > 2时, f `(t ) =  =
= 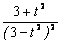 > 0
> 0
∴函数f (t )的单调递减区间是(–1, 1). 4分
(3) 当| t | £ 2时, 由f `(t ) =3 t2 – 3 =0得 t = 1或t = – 1
∵ 1 <| t | £ 2时, f `(t ) > 0
∴ f (t)极大值= f (–1) = 2, f (t)极小值= f (1) = –2
又 f ( 2 ) = 8 – 6 = 2, f (–2) = –8 6 = –2
当 t > 2 时, f (t ) = 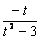 < 0 ,
< 0 ,
又由f `(t ) > 0知f (t )单调递增, ∴ f (t ) > f (2) = –2,
即当 t > 2 时, –2 < f (t ) < 0,
同理可求, 当t < –2时, 有0 < f (t ) < 2,
综合上述得, 当t = –1或t = 2时, f ( t )取最大值2
当t = 1或t = –2时, f ( t )取最小值–2 5分
22.(本小题满分16分)
(1) 当n >1时, bn = Bn –Bn – 1 = 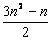 –
– 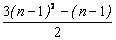 = 3n-2
= 3n-2
令n = 1得b1=1,
∴bn=3n-2. 5分
(2)由an= (1+ 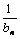 ) a n – 1 ,得
) a n – 1 ,得 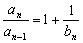 ∴an=
∴an= 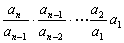
由a1 = 2 ,bn=3n-2知,
an=(1+  )(1
)(1 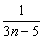 )…(1+
)…(1+ 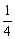 )2
)2
=(1+1)(1+ 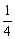 )…(1+
)…(1+  )
)
又 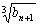 =
= 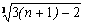 =
= 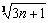 , 5分
, 5分
设cn= 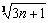 ,
,
当n=1时,有(1+1) = 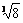 >
> 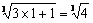
当n=2时,有an=(1+1)(1+ 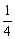 ) =
) = 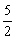 =
= 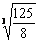 >
> 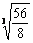 =
= 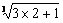 = cn
= cn
假设n=k(k≥1)时an>cn成立,即(1+1)(1+ 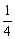 )…(1+
)…(1+ 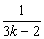 )>
)> 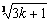 成立,
成立,
则n=k+1时,
左边== (1+1)(1+ 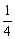 )…(1+
)…(1+ 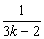 )(1+
)(1+ 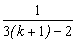 )
)
> 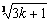 (1+
(1+ 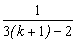 )=
)= 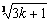
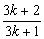 3分
3分
右边= c k 1= 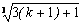 =
= 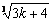
由(ak 1)3 – (c k 1)3 =(3k 1)  –(3k 4) =
–(3k 4) = 
=  >0, 得ak 1 > c k 1成立.
>0, 得ak 1 > c k 1成立.
综合上述, an>cn对任何正整数n都成立. 3分
|