|
不等式的综合应用
不等式是继函数与方程之后的又一重点内容之一,作为解决问题的工具,与其他知识综合运用的特点比较突出.不等式的应用大致可分为两类:一类是建立不等式求参数的取值范围或解决一些实际应用问题;另一类是建立函数关系,利用均值不等式求最值问题、本难点提供相关的思想方法,使考生能够运用不等式的性质、定理和方法解决函数、方程、实际应用等方面的问题.
●难点磁场
(★★★★★)设二次函数f(x)=ax2 bx c(a>0),方程f(x)-x=0的两个根x1、x2满足0<x1<x2< 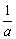 .
.
(1)当x∈[0,x1 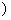 时,证实x<f(x)<x1;
时,证实x<f(x)<x1;
(2)设函数f(x)的图象关于直线x=x0对称,证实:x0< 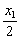 .
.
●案例探究
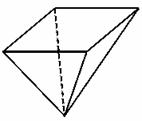 [例1]用一块钢锭烧铸一个厚度均匀,且表面积为2平方米的正四棱锥形有盖容器(如右图)设容器高为h米,盖子边长为a米, [例1]用一块钢锭烧铸一个厚度均匀,且表面积为2平方米的正四棱锥形有盖容器(如右图)设容器高为h米,盖子边长为a米,
(1)求a关于h的解析式;
(2)设容器的容积为V立方米,则当h为何值时,V最大?求出V的最大值(求解本题时,不计容器厚度)
命题意图:本题主要考查建立函数关系式,棱锥表面积和体积的计算及用均值定论求函数的最值.
知识依托:本题求得体积V的关系式后,应用均值定理可求得最值.
错解分析:在求得a的函数关系式时易漏h>0.
技巧与方法:本题在求最值时应用均值定理.
解:①设h′是正四棱锥的斜高,由题设可得:
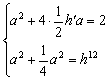 消去
消去 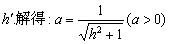
②由 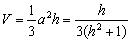 (h>0)
(h>0)
得: 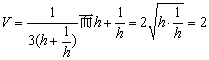
所以V≤ 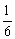 ,当且仅当h=
,当且仅当h= 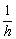 即h=1时取等号
即h=1时取等号
故当h=1米时,V有最大值,V的最大值为 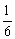 立方米.
立方米.
[例2]已知a,b,c是实数,函数f(x)=ax2 bx c,g(x)=ax b,当-1≤x≤1时|f(x)|≤1.
(1)证实:|c|≤1;
(2)证实:当-1 ≤x≤1时,|g(x)|≤2;
(3)设a>0,有-1≤x≤1时, g(x)的最大值为2,求f(x).
命题意图:本题主要考查二次函数的性质、含有绝对值不等式的性质,以及综合应用数学知识分析问题和解决问题的能力.属★★★★★级题目.
知识依托:二次函数的有关性质、函数的单调性是药引,而绝对值不等式的性质灵活运用是本题的灵魂.
错解分析:本题综合性较强,其解答的要害是对函数f(x)的单调性的深刻理解,以及对条件“-1≤x≤1时|f(x)|≤1”的运用;绝对值不等式的性质使用不当,会使解题过程空洞,缺乏严密,从而使题目陷于僵局.
技巧与方法:本题(2)问有三种证法,证法一利用g(x)的单调性;证法二利用绝对值不等式:||a|-|b||≤|a±b|≤|a| |b|;而证法三则是整体处理g(x)与f(x)的关系.
(1)证实:由条件当=1≤x≤1时,|f(x)|≤1,取x=0得:|c|=|f(0)|≤1,即|c|≤1.
(2)证法一:依题设|f(0)|≤1而f(0)=c,所以|c|≤1.当a>0时,g(x)=ax b在[-1,1]上是增函数,于是
g(-1)≤g(x)≤g(1),(-1≤x≤1).
∵|f(x)|≤1,(-1≤x≤1),|c|≤1,
∴g(1)=a b=f(1)-c≤|f(1)| |c|=2,
g(-1)=-a b=-f(-1) c≥-(|f(-2)| |c|)≥-2,
因此得|g(x)|≤2 (-1≤x≤1);
当a<0时,g(x)=ax b在[-1,1]上是减函数,于是g(-1)≥g(x)≥g(1),(-1≤x≤1),
∵|f(x)|≤1 (-1≤x≤1),|c|≤1
∴|g(x)|=|f(1)-c|≤|f(1)| |c|≤2.
综合以上结果,当-1≤x≤1时,都有|g(x)|≤2.
证法二:∵|f(x)|≤1(-1≤x≤1)
∴|f(-1)|≤1,|f(1)|≤1,|f(0)|≤1,
∵f(x)=ax2 bx c,∴|a-b c|≤1,|a b c|≤1,|c|≤1,
因此,根据绝对值不等式性质得:
|a-b|=|(a-b c)-c|≤|a-b c| |c|≤2,
|a b|=|(a b c)-c|≤|a b c| |c|≤2,
∵g(x)=ax b,∴|g(±1)|=|±a b|=|a±b|≤2,
函数g(x)=ax b的图象是一条直线,因此|g(x)|在[-1,1]上的最大值只能在区间的端点x=-1或x=1处取得,于是由|g(±1)|≤2得|g(x)|≤2,(-1<x<1  .
.
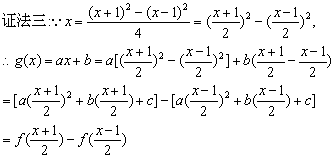
当-1≤x≤1时,有0≤ 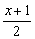 ≤1,-1≤
≤1,-1≤ 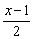 ≤0,
≤0,
∵|f(x)|≤1,(-1≤x≤1),∴|f 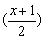 |≤1,|f(
|≤1,|f( 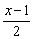 )|≤1;
)|≤1;
因此当-1≤x≤1时,|g(x)|≤|f 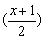 | |f(
| |f( 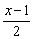 )|≤2.
)|≤2.
(3)解:因为a>0,g(x)在[-1,1]上是增函数,当x=1时取得最大值2,即
g(1)=a b=f(1)-f(0)=2. ①
∵-1≤f(0)=f(1)-2≤1-2=-1,∴c=f(0)=-1.
因为当-1≤x≤1时,f(x)≥-1,即f(x)≥f(0),
根据二次函数的性质,直线x=0为f(x)的图象的对称轴,
由此得- 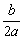 <0 ,即b=0.
<0 ,即b=0.
由①得a=2,所以f(x)=2x2-1.
●锦囊妙计
1.应用不等式知识可以解决函数、方程等方面的问题,在解决这些问题时,要害是把非不等式问题转化为不等式问题,在化归与转化中,要注重等价性.
2.对于应用题要通过阅读,理解所给定的材料,寻找量与量之间的内在联系,抽象出事物系统的主要特征与关系,建立起能反映其本质属性的数学结构,从而建立起数学模型,然后利用不等式的知识求出题中的问题.
●歼灭难点练习
一、选择题
1.(★★★★★)定义在R上的奇函数f(x)为增函数,偶函数g(x)在区间[0, ∞)的图象与f(x)的图象重合,设a>b>0,给出下列不等式,其中正确不等式的序号是( )
①f(b)-f(-a)>g(a)-g(-b) ②f(b)-f(-a)<g(a)-g(-b)
③f(a)-f(-b)>g(b)-g(-a) ④f(a)-f(-b)<g(b)-g(-a)
A.①③ B.②④ C.①④ D.②③
二、填空题
2.(★★★★★)下列四个命题中:①a b≥2 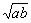 ②sin2x
②sin2x 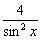 ≥4 ③设x,y都是正数,若
≥4 ③设x,y都是正数,若 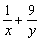 =1,则x y的最小值是12 ④若|x-2|<ε,|y-2|<ε,则|x-y|<2ε,其中所有真命题的序号是__________.
=1,则x y的最小值是12 ④若|x-2|<ε,|y-2|<ε,则|x-y|<2ε,其中所有真命题的序号是__________.
3.(★★★★★)某公司租地建仓库,每月土地占用费y1与车库到车站的距离成反比,而每月库存货物的运费y2与到车站的距离成正比,假如在距车站10公里处建仓库,这两项费用y1和y2分别为2万元和8万元,那么要使这两项费用之和最小,仓库应建在离车站__________公里处.
三、解答题
4.(★★★★★)已知二次函数 f(x)=ax2 bx 1(a,b∈R,a>0),设方程f(x)=x的两实数根为x1,x2.
(1)假如x1<2<x2<4,设函数f(x)的对称轴为x=x0,求证x0>-1;
(2)假如|x1|<2,|x2-x1|=2,求b的取值范围.
5.(★★★★)某种商品原来定价每件p元,每月将卖出n件,假若定价上涨x成(这里x成即 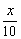 ,0<x≤10
,0<x≤10 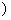 .每月卖出数量将减少y成,而售货金额变成原来的 z倍.
.每月卖出数量将减少y成,而售货金额变成原来的 z倍.
(1)设y=ax,其中a是满足 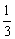 ≤a<1的常数,用a来表示当售货金额最大时的x的值;
≤a<1的常数,用a来表示当售货金额最大时的x的值;
(2)若y= 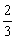 x,求使售货金额比原来有所增加的x的取值范围.
x,求使售货金额比原来有所增加的x的取值范围.
6.(★★★★★)设函数f(x)定义在R上,对任意m、n恒有f(m n)=f(m)·f(n),且当x>0时,0<f(x)<1.
(1)求证:f(0)=1,且当x<0时,f(x)>1;
(2)求证:f(x)在R上单调递减;
(3)设集合A={ (x,y)|f(x2)·f(y2)>f(1)},集合B={(x,y)|f(ax-g 2)=1,a∈R},若A∩B= 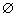 ,求a的取值范围.
,求a的取值范围.
7.(★★★★★)已知函数f(x)= 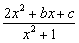 (b<0)的值域是[1,3],
(b<0)的值域是[1,3],
(1)求b、c的值;
(2)判定函数F(x)=lgf(x),当x∈[-1,1]时的单调性,并证实你的结论;
(3)若t∈R,求证:lg 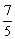 ≤F(|t-
≤F(|t- 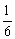 |-|t
|-|t 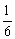 |)≤lg
|)≤lg 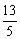 .
.
[科普美文]数学中的不等式关系
数学是研究空间形式和数量关系的科学,恩格斯在《自然辩证法》一书中指出,数学是辩证的辅助工具和表现形式,数学中蕴含着极为丰富的辩证唯物主义因素,等与不等关系正是该点的生动体现,它们是对立统一的,又是相互联系、相互影响的;等与不等关系是中学数学中最基本的关系.
等的关系体现了数学的对称美和统一美,不等关系则如同仙苑奇葩呈现出了数学的奇异美.不等关系起源于实数的性质,产生了实数的大小关系,简单不等式,不等式的基本性质,假如把简单不等式中的实数抽象为用各种数学符号集成的数学式,不等式发展为一个人丁兴旺的大家族,由简到繁,形式各异.假如赋予不等式中变量以特定的值、特定的关系,又产生了重要不等式、均值不等式等.不等式是永恒的吗?显然不是,由此又产生了解不等式与证实不等式两个极为重要的问题.解不等式即寻求不等式成立时变量应满足的范围或条件,不同类型的不等式又有不同的解法;不等式证实则是推理性问题或探索性问题.推理性即在特定条件下,阐述论证过程,揭示内在规律,基本方法有比较法、综合法、分析法;探索性问题大多是与自然数n有关的证实问题,常采用观察—归纳—猜想—证实的思路,以数学归纳法完成证实.另外,不等式的证实方法还有换元法、放缩法、反证法、构造法等.
数学科学是一个不可分割的有机整体,它的生命力正是在于各个部分之间的联系.不等式的知识渗透在数学中的各个分支,相互之间有着千丝万缕的联系,因此不等式又可作为一个工具来解决数学中的其他问题,诸如集合问题,方程(组)的解的讨论,函数单调性的研究,函数定义域的确定,三角、数列、复数、立体几何、解析几何中的最大值、最小值问题无一不与不等式有着密切的联系.许多问题最终归结为不等式的求解或证实;不等式还可以解决现实世界中反映出来的数学问题.不等式中常见的基本思想方法有等价转化、分类讨论、数形结合、函数与方程.总之,不等式的应用体现了一定的综合性,灵活多样性.
等与不等形影不离,存在着概念上的亲缘关系,是中学数学中最广泛、最普遍的关系.数学的基本特点是应用的广泛性、理论的抽象性和逻辑的严谨性,而不等关系是深刻而生动的体现.不等虽没有等的温柔,没有等的和谐,没有等的恰到好处,没有等的天衣无缝,但它如山之挺拔,峰之隽秀,海之宽广,天之高远,怎能不让人心旷神怡,魂牵梦绕呢?
参考答案
难点磁场
解:(1)令F(x)=f(x)-x,因为x1,x2是方程f(x)-x=0的根,所以F(x)=a(x-x1)(x-x2).当x∈(0,x1)时,由于x1<x2,得(x-x1)(x-x2)>0,
又a>0,得F(x)=a(x-x1)(x-x2)>0,即x<f(x)
x1-f(x)=x1-[x F(x)]=x1-x a(x1-x)(x-x2)=(x1-x)[1 a(x-x2)]
∵0<x<x1<x2< 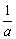 ,∴x1-x>0,1 a(x-x2)=1 ax-ax2>1-ax2>0
,∴x1-x>0,1 a(x-x2)=1 ax-ax2>1-ax2>0
∴x1-f(x)>0,由此得f(x)<x1.
(2)依题意:x0=- 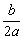 ,因为x1、x2是方程f(x)-x=0的两根,即x1,x2是方程ax2 (b-1)x c=0的根.
,因为x1、x2是方程f(x)-x=0的两根,即x1,x2是方程ax2 (b-1)x c=0的根.
∴x1 x2=- 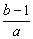
∴x0=- 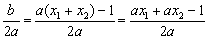 ,因为ax2<1,
,因为ax2<1,
∴x0< 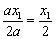
歼灭难点练习
一、1.解析:由题意f(a)=g(a)>0,f(b)=g(b)>0,且f(a)>f(b),g(a)>g(b)
∴f(b)-f(-a)=f(b) f(a)=g(a) g(b)
而g(a)-g(-b)=g(a)-g(b)∴g(a) g(b)-[g(a)-g(b)]
=2g(b)>0,∴f(b)-f(-a)>g(a)-g(-b)
同理可证:f(a)-f(-b)>g(b)-g(-a)
答案:A
二、2.解析:①②③不满足均值不等式的使用条件“正、定、等”.④式:|x-y|=|(x-2)-(y-2)|≤|(x-2)-(y-2)|≤|x-2| |y-2|<ε ε=2ε.
答案:④
3.解析:由已知y1= 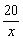 ;y2=0.8x(x为仓库与车站距离)费用之和y=y1 y2=0.8x
;y2=0.8x(x为仓库与车站距离)费用之和y=y1 y2=0.8x 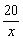 ≥2
≥2 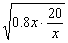 =8
=8
当且仅当0.8x= 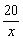 即x=5时“=”成立
即x=5时“=”成立
答案:5公里处
三、4.证实:(1)设g(x)=f(x)-x=ax2 (b-1)x 1,且x>0.
∵x1<2<x2<4,∴(x1-2)(x2-2)<0,即x1x2<2(x1 x2)-4,
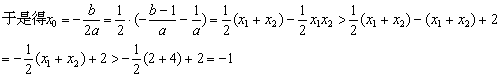
(2)解:由方程g(x)=ax2 (b-1)x 1=0可知x1·x2= 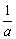 >0,所以x1,x2同号
>0,所以x1,x2同号
1°若0<x1<2,则x2-x1=2,∴x2=x1 2>2,
∴g(2)<0,即4a 2b-1<0 ①
又(x2-x1)2= 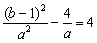
∴2a 1= 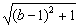 (∵a>0)代入①式得,
(∵a>0)代入①式得,
2 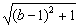 <3-2b ②
<3-2b ②
解②得b< 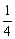
2°若 -2<x1<0,则x2=-2 x1<-2
∴g(-2)<0,即4a-2b 3<0 ③
又2a 1= 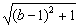 ,代入③式得
,代入③式得
2 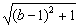 <2b-1 ④
<2b-1 ④
解④得b> 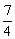 .
.
综上,当0<x1<2时,b< 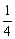 ,当-2<x1<0时,b>
,当-2<x1<0时,b> 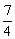 .
.
5.解:(1)由题意知某商品定价上涨x成时,上涨后的定价、每月卖出数量、每月售货金额分别是:p(1 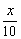 )元、n(1-
)元、n(1- 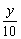 )元、npz元,因而
)元、npz元,因而
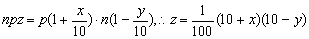 ,在y=ax的条件下,z=
,在y=ax的条件下,z= 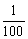 [-a
[-a
[x- 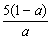 ]2 100
]2 100 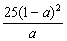 ].由于
].由于 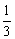 ≤a<1,则0<
≤a<1,则0< 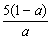 ≤10.
≤10.
要使售货金额最大,即使z值最大,此时x= 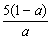 .
.
(2)由z= 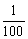 (10 x)(10-
(10 x)(10- 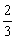 x)>1,解得0<x<5.
x)>1,解得0<x<5.
6.(1)证实:令m>0,n=0得:f(m)=f(m)·f(0).∵f(m)≠0,∴f(0)=1
取m=m,n=-m,(m<0),得f(0)=f(m)f(-m)
∴f(m)= 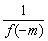 ,∵m<0,∴-m>0,∴0<f(-m)<1,∴f(m)>1
,∵m<0,∴-m>0,∴0<f(-m)<1,∴f(m)>1
(2)证实:任取x1,x2∈R,则f(x1)-f(x2)=f(x1)-f[(x2-x1) x1]
=f(x1)-f(x2-x1)·f(x1)=f(x1)[1-f(x2-x1)],
∵f(x1)>0,1-f(x2-x1)>0,∴f(x1)>f(x2),
∴函数f(x)在R上为单调减函数.
(3)由 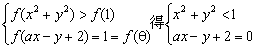 ,由题意此不等式组无解,数形结合得:
,由题意此不等式组无解,数形结合得: 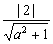 ≥1,解得a2≤3
≥1,解得a2≤3
∴a∈[- 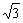 ,
, 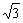 ]
]
7.(1)解:设y= 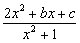 ,则(y-2)x2-bx y-c=0 ①
,则(y-2)x2-bx y-c=0 ①
∵x∈R,∴①的判别式Δ≥0,即 b2-4(y-2)(y-c)≥0,
即4y2-4(2 c)y 8c b2≤0 ②
由条件知,不等式②的解集是[1,3]
∴1,3是方程4y2-4(2 c)y 8c b2=0的两根
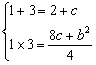 ∴c=2,b=-2,b=2(舍)
∴c=2,b=-2,b=2(舍)
(2)任取x1,x2∈[-1,1],且x2>x1,则x2-x1>0,且
(x2-x1)(1-x1x2)>0,∴f(x2)-f(x1)=- 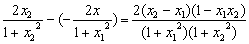 >0,
>0,
∴f(x2)>f(x1),lgf(x2)>lgf(x1),即F(x2)>F(x1)
∴F(x)为增函数.
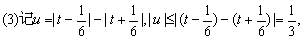
即- 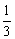 ≤u≤
≤u≤ 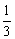 ,根据F(x)的单调性知
,根据F(x)的单调性知
F(- 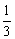 )≤F(u)≤F(
)≤F(u)≤F( 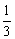 ),∴lg
),∴lg 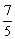 ≤F(|t-
≤F(|t- 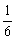 |-|t
|-|t 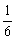 |)≤lg
|)≤lg 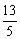 对任意实数t 成立.
对任意实数t 成立.
|