|
高考数学(理科)月考试题卷(三)
试题卷
一:选择题(每题只有一个选择满足要求,每小题5分,共40分)
1: 已知命题 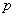 :
: 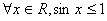 ,则( )
,则( )
A.  B.
B. 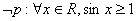
C.  D.
D. 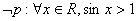
2.函数 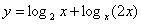 的值域是 ( )
的值域是 ( )
A. 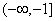 B.
B. 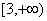 C.
C. 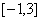 D.
D. 
3.在用数学归纳法证实多边形内角和定理时,第一步应验证( )
(A): n=1, ( B):n=2, (C):n=3 , ( D):n=4
4.有6个座位连成一排,现有3人就坐,则恰有两个空座位相邻的不同坐法有 ( )
A.36种 B.48种 C.72种 D.96种
5.一个等差数列共n项,其和为90,这个数列的前10项的和为25,后10项的和为75,则项数n为 ( )
A.14 B.16 C.18 D.20
6:把函数 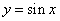 的图象按向量
的图象按向量 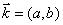 平移后得到函数
平移后得到函数  的图象,则向量
的图象,则向量 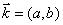 为:
为:
A:  , B:
, B: 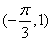 , C:
, C: 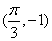 , D:
, D: 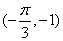 。
。
7.设f(x) = 10x,下列等式中,对于x1 , x2 Î R不恒成立的是( )
(A) f(x1 x2 ) = f( x1 )f( x2 ) (B) 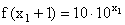
(C) 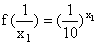 (D)
(D) 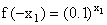
8.4只笔与5本书的价格之和小于22元,而6只笔与3本书的价格之和大于24元,则2只笔与3本书的价格比较( )
A.2只笔贵 B.3本书贵 C.二者相同 D.无法确定
二:填空题(每小题5分,共30分)
9:定义在R上函数f(x)满足f(x 1)=-f(x),若 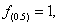 则
则 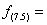
10:二项式  的展开式中的常数项是:
的展开式中的常数项是:
11:已知函数 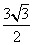 为增函数,则a的取值范围是:
为增函数,则a的取值范围是:
12:已知函数f(x)满足:f(p q)=f(p)f(q), f(1)=3,则
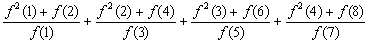 = .
= .
(从下列3题中选做两题,若全做的按前两题记分)
13::若 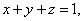 则
则 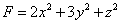 的最小值为: 。
的最小值为: 。
14:已知圆O直径为10,AB是圆O的直径,C为圆O上一点,且BC=6,过点B的圆O的切线交AC延长线于点D,则DA=
15:曲线  与曲线
与曲线 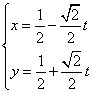 的位置关系是:
的位置关系是:
三:解答题(共80分)
16、(12分)从4名男生和2名女生中任选3人参加演讲比赛,试求:
(1)所选3人都是男生的概率。
(2)所选3人中恰有1名女生的概率。
(3)所选3人中至少有1名女生的概率。
17、(12分)在  中,
中,  、
、 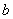 、
、 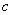 分别为
分别为 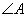 、
、  、
、 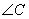 的对边,已知
的对边,已知  ,
, 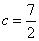 ,三角形面积为
,三角形面积为 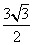 。
。
(1)求 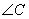 (2)
(2) 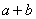
18、(14分)某公司要将一批不易存放的蔬菜从A地运到B 地,有汽车、火车两种运输工具可供选择,两种运输工具的主要参考数据如下表:
|
运输工具 |
途中速度
(km/h) |
途中费用
(元/km) |
装卸时间
(h) |
装卸费用
(元) |
|
汽车 |
50 |
8 |
2 |
1000 |
|
火车 |
100 |
4 |
4 |
2000 |
若这批蔬菜在运输过程(含装卸时间)中损耗为300元/h,试根据A、B 两地距离大小比较采用哪种运输工具较好(即运输过程中的费用与损耗费用之和最小)?
19、(14分)已知函数 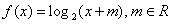
(1)若 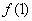 ,
, 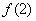 ,
, 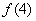 成等差数列,求m的值。
成等差数列,求m的值。
(2)若  、
、 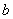 、
、 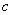 是两两不相等的正数,且
是两两不相等的正数,且  、
、 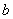 、
、 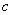 依次成等差数列,试判定
依次成等差数列,试判定 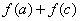 与
与  的大小关系,并证实你的结论。
的大小关系,并证实你的结论。
20、(14分)已知  在区间
在区间 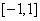 上是增函数
上是增函数
(1)求实数  的值组成的集合A;
的值组成的集合A;
(2)设关于 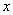 的方程
的方程 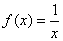 的两个非零实根为
的两个非零实根为 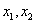 。
。
试问:是否存在实数m,使得不等式  对
对 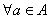 及
及  恒成立?若存在,求m的取值范围;若不存在,请说明理由。
恒成立?若存在,求m的取值范围;若不存在,请说明理由。
21、(14分)设 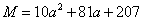 ,
,  ,Q=
,Q= 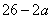 ;若将
;若将 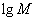 ,lgQ,lgP适当排序后可构成公差为1的等差数列
,lgQ,lgP适当排序后可构成公差为1的等差数列  的前三项
的前三项
(1)试比较M,P,Q的大小。
(2)求  的值及
的值及  的通项;
的通项;
(3)记函数 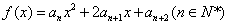 的图象在
的图象在 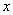 轴上截得的线段长为
轴上截得的线段长为 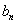 ,设
,设 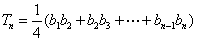 ,
, 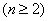
求 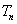 ,并证实
,并证实 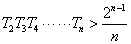
数学(理科)试题答题卷
二、填空题(每小题5分,共30分)
9、__________________;10、__________________;11、__________________;
12、__________________;
13、__________________;14、__________________; 15: __________________;
三、解答题(共80分)
16、(12分)
17、(12分)

18、(14分)

19、(14分)


|
姓名:____________班级:____________学号:____________ |  20、(14分) 20、(14分)

 21、(14分) 21、(14分)
12月月考答案
一:CDCCC,ACA.
(8)设每支笔x元,每本书y元,有 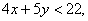
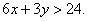
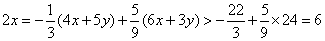
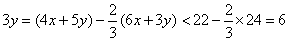
二:(9): -1; (10):15; (11)[—3,3]; (12):24;
(13) 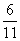 ; (14):
; (14):  ; (15):相交
; (15):相交
三:16、(本题12分)
解:从4名男生和2名女生中任选3人共有 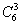 种等可能结果…………1分
种等可能结果…………1分
(1)设A={所选3人都是男生},则A中含有  种结果
种结果
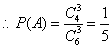 ………………………………………………………4分
………………………………………………………4分
(2)设B={所选3人中恰有1名女生},则B中含有 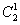
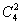 种结果
种结果
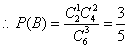 ……………………………………………………7分
……………………………………………………7分
(3)设C={所选3人中至少有1名女生},则C与A对立
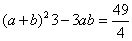 …………………………………………11分
…………………………………………11分
答:(1)所选3人都是男生的概率为 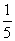
(2)所选3人恰有1名女生的概率为 
(3)所选3人至少1名女生的概率为  ……………………………12分
……………………………12分
17、解:(1)由条件的 

 ………………………………………4分
………………………………………4分
又  ………………………………………………………………5分
………………………………………………………………5分
 …………………………………………………………………6分
…………………………………………………………………6分
(2)由余弦定理及 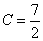 得
得
 ,即
,即 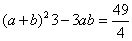 ……………①…………8分
……………①…………8分
又由 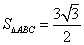 即
即  得
得  …②…………10分
…②…………10分
 由①②消去
由①②消去  解得
解得 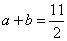 ……………………………………………12分
……………………………………………12分
18、(14分)解:设A、B两地相离 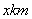 ,则
,则
用汽车运输的总支出为:
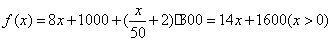 ………………………4分
………………………4分
用火车运输的总支出为:
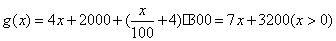 ………………………8分
………………………8分
(1)由 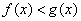 得
得 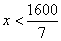
(2)由  得
得 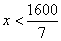
(3)由 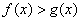 得
得 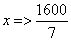 …………………………………………12分
…………………………………………12分
答:当A、B两地距离小于  时,采用汽车运输好
时,采用汽车运输好
当A、B两地距离等于  时,采用汽车或火车都一样
时,采用汽车或火车都一样
当A、B两地距离大于  时,采用火车运输好………………14分
时,采用火车运输好………………14分
19、(14分)解:(1) 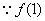 、
、 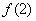 、
、 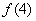 成等差数列
成等差数列
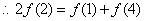 ,即
,即  2分
2分
解得  …………………………………………………………4分
…………………………………………………………4分
(2) 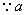 ,
, 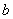 ,
, 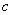 成等差数列
成等差数列
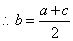 …………………………………①………………………6分
…………………………………①………………………6分
又  ,
, 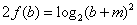
而 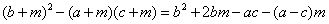 ……………………8分
……………………8分

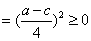 …………………………………12分
…………………………………12分

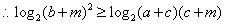
故 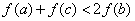 (因为
(因为  )…………………………14分
)…………………………14分
20、(14分)解:(1) 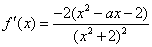 …………………………………1分
…………………………………1分
 在
在 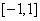 上是增函数
上是增函数
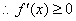 即
即 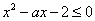 ,在
,在 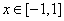 恒成立 …………①…………3分
恒成立 …………①…………3分
设 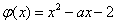 ,则由①得
,则由①得
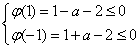 解得
解得 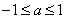
 ………………………………………………………6分
………………………………………………………6分
(2)由 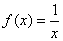 即
即 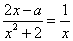 得
得 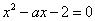

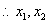 是方程
是方程 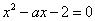 的两个非零实根
的两个非零实根
 ,
, 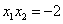 ,又由
,又由 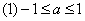
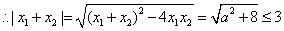 ……………………………9分
……………………………9分
于是要使  对
对 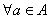 及
及  恒成立
恒成立
即 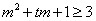 即
即 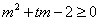 对
对 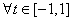 恒成立 ………②………11分
恒成立 ………②………11分
设 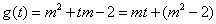 ,则由②得
,则由②得
 解得
解得  或
或 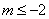
故存在实数  满足题设条件…………………………14分
满足题设条件…………………………14分
21、(14分)解:(1)由 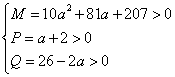 得
得 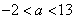 ……………2分
……………2分
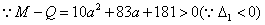 ………………………3分
………………………3分
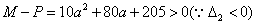 ………………………4分
………………………4分
 ,
, 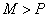
又  当
当 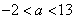 时,
时, 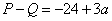 ,
,
当 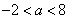 时,即
时,即 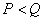 ,则
,则 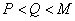 ………………………5分
………………………5分
当  时,
时, 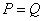 ,则
,则 
当 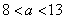 时,
时, 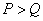 ,则
,则 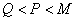
(2)依题 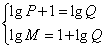 即
即 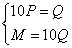

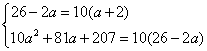
解得  ,从而
,从而  ………………………8分
………………………8分
(3) 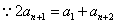 ,设
,设  与
与 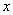 轴交点为
轴交点为 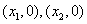
 当
当  =0时有
=0时有 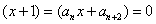
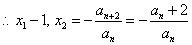 ………………………………………9分
………………………………………9分
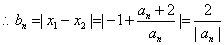
又 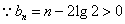 ,
, 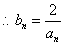

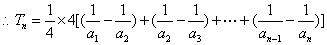
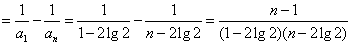 …………11分
…………11分

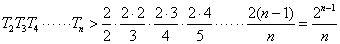 …………14分
…………14分
|