|
高考理科数学测试试题
数学试卷(理科)
一、选择题:(本大题共8个小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.若集合 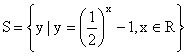 ,
,  ,则
,则 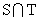 等于( )
等于( )
A.{0} B. 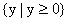 C.T D. S
C.T D. S
2. 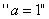 是“函数
是“函数 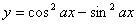 \* MERGEFORMAT
的最小正周期为
\* MERGEFORMAT
的最小正周期为 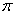 \* MERGEFORMAT
”的 ( ).
\* MERGEFORMAT
”的 ( ).
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
3.设  是方程
是方程 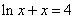 的解,则
的解,则  属于区间( )
属于区间( )
A. (0,1) B. (1,2) C. (2,3) D.(3,4)
4.有6个座位连成一排,现有3人就坐,则恰有两个空座位相邻的不同坐法有 ( )
A.36种 B.48种 C.72种 D.96种
5.一个等差数列共n项,其和为90,这个数列的前10项的和为25,后10项的和为75,则项数n为 ( )
A.14 B.16 C.18 D.20
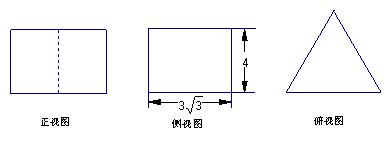 6.若一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如下图所示,则这个棱柱的体积为 ( ) 6.若一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如下图所示,则这个棱柱的体积为 ( )
A. 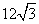 B.
B. 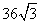 C.
C. 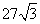 D. 6
D. 6
7.已知某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图(如图所示),则甲、乙两人得
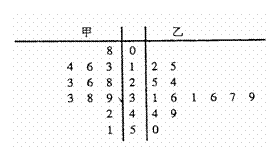 分的中位数之和是 ( ) ( ) 分的中位数之和是 ( ) ( )
A.62
B.63
C.64
D.65
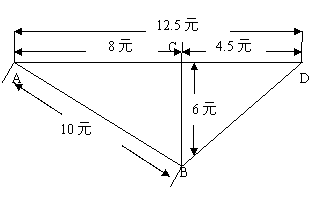 8. A,B,C,D四个城市之间有笔直的公路相连接,客运车行驶于各城市之间,其票价与路程成正比.具体票价如图,则BD之间的票价应为( ) 8. A,B,C,D四个城市之间有笔直的公路相连接,客运车行驶于各城市之间,其票价与路程成正比.具体票价如图,则BD之间的票价应为( )
A、7.5元 B、7元
C、8元 D、8.5元
二、填空题:(本大题共6个小题,每小题5分,共30分,其中9-12题必做,在13,14,15题中选做两题,多选以前两题计分,把答案写在答题卷上).
9. 已知  ,若
,若  ,则
,则 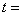
10.二项式 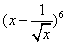 的展开式中的常数项是
的展开式中的常数项是
11.随机地向半圆 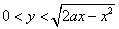 (
( 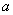 为正常数)内掷一点,点落在圆内任何区域的概率与区域的面积成正比,则原点与该点的连线与
为正常数)内掷一点,点落在圆内任何区域的概率与区域的面积成正比,则原点与该点的连线与 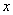 轴的夹角小于
轴的夹角小于  的概率为 .
的概率为 .
12.已知函数f(x)满足:f(p q)=f(p)f(q), f(1)=3, 则
 = .
= .
13、极坐标方程 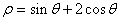 所表示的曲线的直角坐标方程是 .
所表示的曲线的直角坐标方程是 .
 14、已知 14、已知 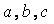 都是正数,且
都是正数,且 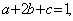 则
则  的最小值是 .
的最小值是 .
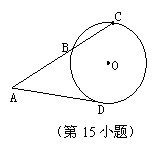
15.已知圆 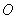 的半径为
的半径为 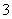 ,从圆
,从圆 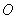 外一点
外一点  引切线
引切线  和割线
和割线 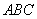 ,
,
圆心 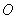 到
到 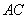 的距离为
的距离为 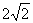 ,
,  ,则切线
,则切线  的长
的长
为 _______.
三.解答题:本大题共6小题,共80分.解答应写出文字说明,证实过程或演算步骤.
16.(本题满分(12分)
已知向量 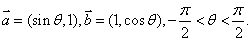 \* MERGEFORMAT
\* MERGEFORMAT
(I)若 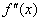 \* MERGEFORMAT
求
\* MERGEFORMAT
求 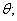 \* MERGEFORMAT
(II)求
\* MERGEFORMAT
(II)求 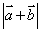 \* MERGEFORMAT
的最大值。
\* MERGEFORMAT
的最大值。
17.(本题满分(12分)已知函数  是定义在
是定义在 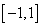 上的奇函数,在
上的奇函数,在 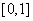 上
上 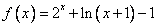 .
.
(Ⅰ)求函数  的解析式;并判定
的解析式;并判定  在
在 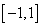 上的单调性(不要求证实)
上的单调性(不要求证实)
(Ⅱ)解不等式 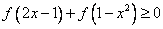 .
.
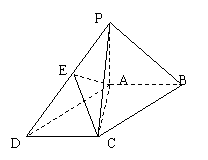 18.(本题满分14分)如图,在底面为平行四边形的四棱锥 18.(本题满分14分)如图,在底面为平行四边形的四棱锥  中,
中, 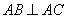 ,
,  平面
平面 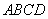 ,且
,且  ,点
,点 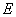 是
是 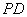 的中点.(Ⅰ)求证:
的中点.(Ⅰ)求证: 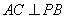 ; (Ⅱ)求证:
; (Ⅱ)求证: 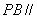 平面
平面  ;(Ⅲ)求二面角
;(Ⅲ)求二面角 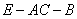 的大小.
的大小.
19.(本题满分14分)已知直线 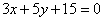 与
与 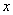 轴和
轴和  轴分别交于A、B两点,椭圆O以原点为中心,A、B为顶点,点C的坐标是
轴分别交于A、B两点,椭圆O以原点为中心,A、B为顶点,点C的坐标是 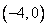 ,点D的坐标是
,点D的坐标是 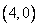 点P在椭圆O第一象限的部分上.
点P在椭圆O第一象限的部分上.
(1)求椭圆O的方程;(2)若 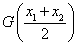 求点P的坐标;(3)求△PAB面积的最大值.
求点P的坐标;(3)求△PAB面积的最大值.
20.(本小题满分14分)一个蜂巢里有一只蜜蜂,第一天,它飞出去找回了 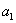 个伙伴;第二天,它又飞出去,找回了
个伙伴;第二天,它又飞出去,找回了 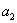 个伙伴……,第n天,它又飞出去,找回了
个伙伴……,第n天,它又飞出去,找回了  个伙伴,已知这只蜜蜂在这n天中它找到的伙伴总数
个伙伴,已知这只蜜蜂在这n天中它找到的伙伴总数 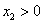 满足:
满足: 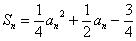 .
.
(Ⅰ)求这只蜜蜂第1天中它找的伙伴数 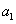 及这只蜜蜂在第n天中它找的伙伴数
及这只蜜蜂在第n天中它找的伙伴数  .
.
(Ⅱ)从第一天起,若这只蜜蜂找回的伙伴在家(蜂巢)建造小蜂房,已知第一天建造了 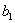 个小蜂房,第二天建造了
个小蜂房,第二天建造了 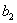 个小蜂房……,第n天建造了
个小蜂房……,第n天建造了  个小蜂房;问数列
个小蜂房;问数列 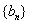 是否是等比数列,使得
是否是等比数列,使得  成立(
成立(  ),若是,请求出数列
),若是,请求出数列 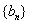 ;若不是,请说明理由。
;若不是,请说明理由。
21.(本题满分14分)对于三次函数 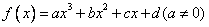 ,定义:设
,定义:设 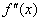 是函数
是函数 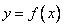 的导函数
的导函数  的导数,若
的导数,若 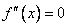 有实数解
有实数解  ,则称点
,则称点 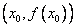 为函数
为函数 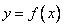 的“拐点”。现已知
的“拐点”。现已知 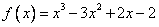 ,请解答下列问题:
,请解答下列问题:
(Ⅰ)求函数  的“拐点”A的坐标;
的“拐点”A的坐标;
(Ⅱ)求证  的图象关于“拐点”A 对称;并写出对于任意的三次函数都成立的有关“拐点”的一个结论(此结论不要求证实);
的图象关于“拐点”A 对称;并写出对于任意的三次函数都成立的有关“拐点”的一个结论(此结论不要求证实);
(Ⅲ)若另一个三次函数G(x)的“拐点”为B(0,1),且一次项系数为0,当 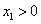 ,
, 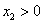
 时,试比较
时,试比较  与
与 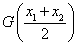 的大小。
的大小。
答案
一、选择题:1. D. 2.C 3.C 4.C 5.C 6.B 7. B 8.A
二、填空题:9. 3 10. 15 11.  12. 24 13.
12. 24 13. 
14.  15.
15. 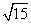
三.解答题:
16.(本题满分 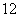 分)
分)
解析:(1) 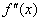 \* MERGEFORMAT
\* MERGEFORMAT
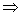 \* MERGEFORMAT
\* MERGEFORMAT
 \* MERGEFORMAT
\* MERGEFORMAT
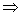 \* MERGEFORMAT
\* MERGEFORMAT
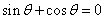 \* MERGEFORMAT
\* MERGEFORMAT
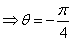 \* MERGEFORMAT
;
\* MERGEFORMAT
;
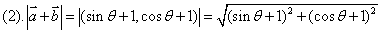 \* MERGEFORMAT
\* MERGEFORMAT
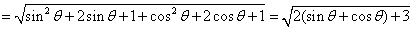 \* MERGEFORMAT
\* MERGEFORMAT
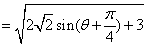 \* MERGEFORMAT
\* MERGEFORMAT
当 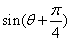 \* MERGEFORMAT
=1时
\* MERGEFORMAT
=1时 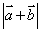 \* MERGEFORMAT
有最大值,此时
\* MERGEFORMAT
有最大值,此时  \* MERGEFORMAT
,最大值为
\* MERGEFORMAT
,最大值为 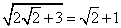 \* MERGEFORMAT
。
\* MERGEFORMAT
。
17. 解:(1) 设 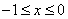 ,则
,则 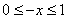 …………………1分
…………………1分
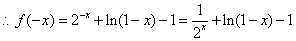 …………………2分
…………………2分
又 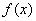 是奇函数,所以
是奇函数,所以 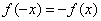 …………………3分
…………………3分
 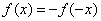 =
= 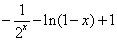 ……4分
……4分
………………5分
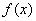 是[-1,1]上增函数 ………………6分
是[-1,1]上增函数 ………………6分
(2) 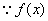 是[-1,1]上增函数,由已知得:
是[-1,1]上增函数,由已知得: 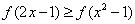 …………7分
…………7分
等价于 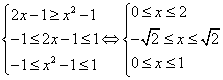 …………10分
…………10分
解得:  ,所以
,所以  …………12分
…………12分
18.解:(1)由  平面
平面 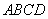 可得PA^AC
可得PA^AC
又 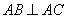 ,所以AC^平面PAB,所以
,所以AC^平面PAB,所以
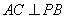
(2)如图,连BD交AC于点O,连EO,则
EO是△PDB的中位线,\EO 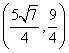 PB
PB
\PB 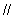 平面
平面 
(3)如图,取AD的中点F,连EF,FO,则EF是△PAD的中位线,
\EF 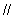 PA又
PA又  平面
平面 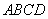 ,\EF^平面
,\EF^平面 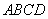
同理FO是△ADC的中位线,\FO 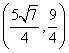 AB\FO^AC由三垂线定理可知\ÐEOF是二面角E-AC-D的平面角.又FO=
AB\FO^AC由三垂线定理可知\ÐEOF是二面角E-AC-D的平面角.又FO= 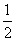 AB=
AB= 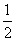 PA=EF\ÐEOF=45°而二面角
PA=EF\ÐEOF=45°而二面角 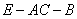 与二面角E-AC-D互补,故所求二面角
与二面角E-AC-D互补,故所求二面角 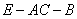 的大小为135°.
的大小为135°.
19、A、B两点分别为(-5,0),(0,-3)即长轴在x轴, 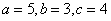
 椭圆的方程为
椭圆的方程为 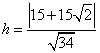 ................................................................................. 4分
................................................................................. 4分
(2)设点P坐标为 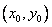
法一:  点P在椭圆O第一象限的部分上
点P在椭圆O第一象限的部分上
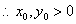 .......................................................................................................... 5分
.......................................................................................................... 5分
由 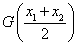 得:
得:  ........................... 6分
........................... 6分
与椭圆方程联立得 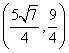 ................................................................................ 8分
................................................................................ 8分
法二:由 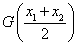 得
得 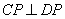
 P点在以CD为直径的圆
P点在以CD为直径的圆 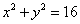 上......... 6分
上......... 6分
与椭圆方程联立得 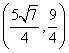 ................................................................................ 8分
................................................................................ 8分
(3)法一:设P点坐标为 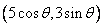 ,则P点到直线AB的距离:
,则P点到直线AB的距离:
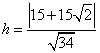
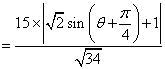
当  时P点在第一象限,此时d取得最大值
时P点在第一象限,此时d取得最大值 
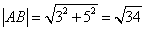
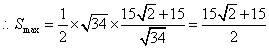 ...................... 14分
...................... 14分
法二:设直线  与椭圆相切,联立方程组得:
与椭圆相切,联立方程组得:
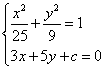

(2)代入(1)得: 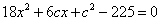
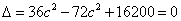
解得: 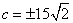
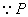 点在第一象限
点在第一象限 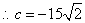
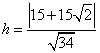 ,
, 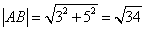
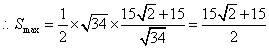 .......................................................... 14分
.......................................................... 14分
20.解:(Ⅰ)∵ 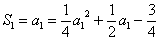 ,
, 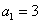 或
或 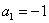 (舍去),
(舍去),
故 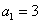 ;………………2分
;………………2分
∵ 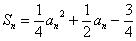 ……………………………①
……………………………①
∴  …………………………………②
…………………………………②
①式减②式得: 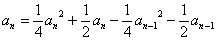 ,
, 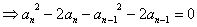
 ,
,
∵ 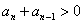 ,∴
,∴ 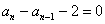 ,即
,即  (
( 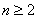 且
且  )
)
∴ 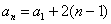
又 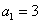
∴ 
∴这只蜜蜂在第n天中它找的伙伴数是 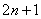 .………………………………………7分
.………………………………………7分
(Ⅱ)假设存在等比数列 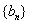
使 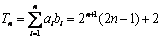 成立
成立
∴当  时,
时,  ;……10分
;……10分
当 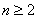 时,
时, 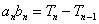 ,即
,即 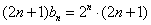 ,所以,
,所以, 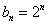 ……12分
……12分
∴存在等比数列 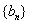 为
为 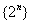 ,使得
,使得  成立(
成立(  ))…14分
))…14分
21 解:(1)  ………………………………1分
………………………………1分
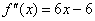
令  得
得  ………………………2分
………………………2分

 拐点
拐点 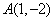 ……………………………………3分
……………………………………3分
(2)设  是
是  图象上任意一点,则
图象上任意一点,则 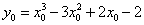 ,因为
,因为  关于
关于 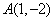 的对称点为
的对称点为  ,把
,把 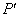 代入
代入  得左边
得左边 
|