第二学期初三数学开学测试
测试试题
一、选择题(本大题共8小题，每小题4分，共32分，在每小题给出的四个选项中，只有一项是符合题意的)
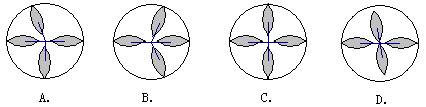
　　1．在下列各图中，既是轴对称图形又是中心对称图形的是(　).
　　

　　2．有9张相同的卡片，上面写有汉字：“我、努、力、我、收、获、我、快、乐”，9张卡片任意搅乱
　 　　后，一个人随机抽取一张，卡片上写有汉字“我”的概率是(　).
　　A. 　　　B. 　　　C. 　　　D.

　　3．两个圆的半径分别是2cm和7cm，圆心距是5cm，则这两个圆的位置关系是(　).
　　A.外离 　　　B.内切　　　 C.相交　　　 D.外切

　　4．在Rt△ABC中，∠C=90°，，则等于(　).
　　A. 　　　B. 　　　C. 　　　D.

　　5．将二次函数的图象先向右平移2个单位，再向下平移3个单位，得到的函数图象的解析式
　 　　是(　).
　　A. 　　　　　B.
　　C. 　　　　　D.

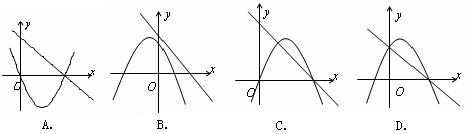
　　6．在同一坐标系中，直线和抛物线的图象只可能是(　).
　　

　　7．如下图，量角器外沿上有A、B两点，它们的读数分别是70°、40°，则∠1的度数为(　).
　　　　　　　　　　　　　　　　　　　　　
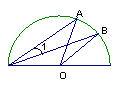
　　A.30°　　　 B.25°　　　 C.15°　　　 D.20°

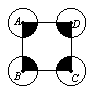
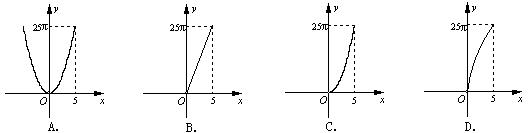
　　8．如右图，正方形ABCD的边长为10，四个等圆的圆心分别在正方形ABCD的顶点上.
　 　　若圆的半径为x，且0＜x ≤5，图中四个阴影部分面积的和为y，则能反映y与x之
　 　　间函数关系的大致图象是(　).
　　

二、填空题(本大题共4小题，每小题4分，共16分)
　　9．据调查，北京市机动车拥有量2005年底达到了近260万辆，而截至2007年底，北京市机动车拥有量已
　 　　达到了近314.6万辆，如果假设2005年至2007年北京市机动车拥有量每年的增长率相同，则此增长率
　 　　为______________.

　　10．已知关于的方程有两个实数根，则k的取值范围为______________.

　　11．某个立体图形的三视图如下，则这个立体图形的表面积为______________平方厘米.
　　　　　　　　　　　　　　　

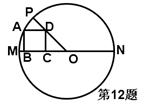
　　12．如图，已知在⊙中，直径，正方形ABCD的四个顶点分别在半径OM、OP以及⊙上，并且
　 　　 ，则AB的长为______________.
　　　　　　　　　　　　　　　　　　　

三、解答题(本题共25分，每小题5分)
　　13．计算：.

　　14．用配方法解方程：.

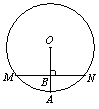
　　15．如图，在⊙O中，弦MN=12，半径OA⊥MN，垂足为B，AB=3，求OA的长.
　　　　　　　　　　　　　　　　　　　　　

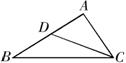
　　16．已知：如图，若AD=3cm，AB=7cm，AC=cm，试证：∠ABC=∠ACD.
　　　　　　　　　　　　　　　　　　　　

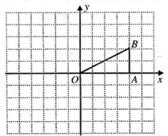
　　17．如图，在中，，且点的坐标为(4，2).
　　(1)画出绕点逆时针旋转后的；
　　(2)求点旋转到点所经过的路线长.
　　　　　　　　　　　　　　　　　　　

四、解答题(本题共47分)
　　18．(本小题满分5分)彤彤和朵朵玩纸牌游戏.下图是同一副扑克中的4张扑克牌的正面，将它们正面朝下洗匀后放在桌上，彤彤先从中抽出一张，朵朵从剩余的3张牌中也抽出一张.彤彤说：若抽出的两张牌的数字都是偶数，你获胜；否则，我获胜.
　　　　　　　　　　　　　　
　　(1)请用树状图或列表法表示出两人抽牌可能出现的所有结果；
　　(2)若按彤彤说的规则进行游戏，这个游戏公平吗？请说明理由.

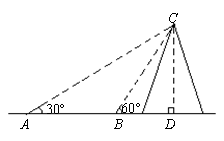
　　19．(本小题满分5分)如图，小明为了测量一铁塔的高度CD，他先在A处测得塔顶C的仰角为，再向塔的方向直行40米到达B处，又测得塔顶C的仰角为，请你帮助小明计算出这座铁塔的高度.(小明的身高忽略不计，结果精确到0.1米，参考数据：，，)
　　　　　　　　　　　　　　　

　　20．(本小题满分6分)已知二次函数，自变量的部分取值及对应的函数值如下表所示：
x … 0 2 …
y … 1 11 …
　　(1)求这个二次函数的解析式；
　　(2)写出这个二次函数图象的顶点坐标.
　　(3)若＞0，且，两点都在该函数的图象上，试比较与的大小.

　　21．(本小题满分5分)如图，⊙O的直径AB交弦CD于点M，且M是CD的中点.过点B作BE∥CD，交AC的延长线于点E.连接BC.
　　(1)求证：BE为⊙O的切线；
　　(2)如果CD=6，tan∠BCD=，求⊙O的直径的长.
　　　　　　　　　　　　　　　　　

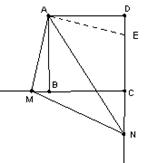
　　22．(本小题满分5分)已知：正方形中，，绕点顺时针旋转，它的两边分别交(或它们的延长线)于点.
　　(1)当绕点旋转到时(如图1)，线段和之间有怎样的数量关系？请直
　 　　接写出你的猜想.
　　(2)当绕点旋转到如图2的位置时，线段和之间又有怎样的数量关系？写出猜
　 　　想，并加以证明.
　　　　　　　　　　　　　　　

　　23．(本小题满分5分)已知：关于x的一元二次方程.
　　(1)求证：方程有两个实数根；
　　(2)设m＜0，且方程的两个实数根分别为，(其中)，若y是关于m的函数，且，
　 　　求这个函数的解析式；

　　24．(本小题满分8分)已知：在△ABC中，∠ABC=90°，点E在直线AB上，ED与直线AC垂直，垂足为D，且点M为EC中点，连接BM、DM.
　　(1)如图1，若点E在线段AB上，探究线段BM与DM及∠BMD与∠BCD所满足的数量关系，并直接写出你得到
　 　　的结论；
　　(2)如图2，若点E在BA延长线上，你在(1)中得到的结论是否发生变化？写出你的猜想并加以证明；
　　(3)若点E在AB延长线上，请你根据条件画出相应的图形，并直接写出线段BM与DM及∠BMD与∠BCD所满足
　 　　的数量关系.
　　　　　　　　　

　　25．(本小题满分8分)在平面直角坐标系中，以点为圆心、5为半径的圆与轴相交于点、(点B在点C的左边)，与轴相交于点D、M(点D在点M的下方).
　　(1)求以直线为对称轴，且经过点D、C的抛物线的解析式；
　　(2)若点P是这条抛物线对称轴上的一个动点，求PC+PD的取值范围；
　　(3)若E为这条抛物线对称轴上的点，则在抛物线上是否存在这样的点F，使得以点B、C、E、F为顶点的
　 　　四边形是平行四边形.若存在，求出点F的坐标；若不存在，说明理由.

参考答案：
一、选择题
　　1.C 2.B 3.B 4.C 5.D 6.C 7.C 8.C

二、填空题
　　9.10% 　　　10. 　　　11. 　　　12.

三、解答题
　　13．原式=

　　14．解：移项，得 ……………1分
　　　　　　二次项系数化为1，得 ……………2分
　　　　　　配方 ……………3分
　　　　　　……………4分
　　　　　　由此可得
　　　　　　，……………5分

　　15．解：连结ON. ………………………………………………1分
　　　　　　∵OA⊥MN于点B，∴. ………………2分
　　　　　　设ON=x，则OB=x-3.
　　　　　　在Rt△中，ON2=OB2+BN2，
　　　　　　∴ …………………………………………………………4分
　　　　　　解得， 即. ………………………………………5分

　　16．解：AD=3cm，AB=7cm，AC=cm
　　　　　　∴……………2分
　　　　　　在中，
　　　　　　，=.……………3分
　　　　　　∴∽……………4分
　　　　　　∴∠ABC=∠ACD……………5分

　　17．解：(1)图略………3分
　　　　　　(2) 点A旋转到点A1所经过的路线长=…………5分

四、解答题
　　18．解：(1)
　　　　　　　　　　　　　　　　　
　　　　　　　 共有12种可能结果. ·························· 2分
　　　　　　(2)游戏公平. ··························· 3分
　　　　　　　 ∵ 两张牌的数字都是偶数有6种结果：
　　　　　　　 (6，10)，(6，12)，(10，6)，(10，12)，(12，6)，(12，10).
　　　　　　　 ∴P(彤彤获胜)==. ······················· 4分
　　　　　　　 P(朵朵获胜)=.·························· 5分
　　　　　　　 ∴ 游戏公平.

　　19．解：∵∠CBD=60°，∠CAB=30°， ∴∠ACB=30°.
　　　　　　∴AB=BC=40.……………2分
　　　　　　在Rt△BDC中，
　　　　　　∴(米)………4分
　　　　　　答：这座铁塔的高度约为34.6米.…………5分

　　20．解：(1)依题意，得 ………………………………2分
　　　　　　　 解得 ………………………………………………………3分
　　　　　　　 ∴为所求. …………………………………………4分
　　　　　　(2)顶点坐标为(，).…………………………………………5分
　　　　　　(3)因为当时，随着的增大而增大；且＞0，
　　　　　　　 ，两点都在该函数的图象上，
　　　　　　　 所以＞.……………………………… 6分

　　21．解：(1)证明：∵AB是⊙O的直径，M是CD的中点，
　　　　　　　　　　 ∴CD⊥AB. ………………………………………………………… 1分
　　　　　　　　　　 ∴∠AMC=90°.
　　　　　　　　　　 ∵BE∥CD，∴∠AMC=∠ABE. ∴∠ABE=90°，即AB⊥BE.
　　　　　　　　　　 又∵B是⊙O上的点，
　　　　　　　　　　 ∴BE是⊙O的切线. ……………………………………………………… 2分
　　　　　　(2)∵M是CD的中点，CD=6，
　　　　　　　 ∴CM=CD=3.
　　　　　　　 在Rt△BCM中，，
　　　　　　　 ∴BM=. …………………………………………………… 3分
　　　　　　　 又∵AB是⊙O的直径， ∠ACB=90°.
　　　　　　　 ∵CM⊥AB于M， ∴Rt△AMC∽Rt△CMB.
　　　　　　　 ∴， ∴.
　　　　　　　 ∴.
　　　　　　　 ∴AM=6. …………………………………………………… 4分
　　　　　　　 ∴AB=AM+BM=6+=. ……………………………………………… 5分
　　　　　　　 即：⊙O的直径的长为.

　　22．解：(1).…………1分
　　　　　　(2).
　　　　　　　 如图，在DC的上截得DE=MB，连接AE，
　　　　　　　 易证： ≌.
　　　　　　　 ∴AE=AM.
　　　　　　　 ∴∠MAB=∠EAD.
　　　　　　　 ∵∠MAN=45°∠BAD=90°
　　　　　　　 ∴∠MAN=∠EAN=45°.
　　　　　　　 又AM为公共边，
　　　　　　　 ∴≌……………4分
　　　　　　　 ∴MN=NE.
　　　　　　　 ∴.……………5分

　　23．(1)证明：∵ 是关于x的一元二次方程，
　　　　　　　　 ………………………………… 1分
　　　　　　　 　∵ m2≥0，
　　　　　　　 　∴ 原方程有两个实数根. ………………………………………………… 2分
　　　　(2)解：由求根公式，得.
　　　　　　　 ∴ x=m+1或x=1. …………………………………………… 3分
　　　　　　　 ∵ m＜0， ∴ m+1＜1.
　　　　　　　 ∵ ，
　　　　　　　 ∴ x1=m+1， x2=1. ……………………………………………………4分
　　　　　　　 ∴ .
　　　　　　　 即(m＜0)为所求. …………………………………………… 5分
　　说明：若第(1)问直接求出两根，累计得3分；第(2)问没写m＜0不扣分；

　　24．解：(1) 结论：BM=DM，∠BMD=2∠BCD. …………………………………2分
　　　　　　(2)在(1)中得到的结论仍然成立. 即BM=DM，∠BMD=2∠BCD.
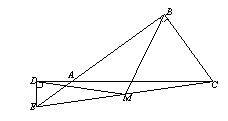
　　　　　　　 证法一：∵ 点M是Rt△BEC的斜边EC的中点，
　　　　　　　 　　　　∴ BM=EC=MC.
　　　　　　　 　　　　又 点M是Rt△DEC的斜边EC的中点，
　　　　　　　 　　　　∴ DM=EC=MC.
　　　　　　　 　　　　∴ BM=DM. ……………………………………………………………3分
　　　　　　　 　　　　∵ BM=MC， DM=MC，
　　　　　　　 　　　　∴ ∠CBM =∠BCM， ∠DCM=∠CDM. …………………………………4分
　　　　　　　 　　　　∴ ∠BMD=∠EMB∠EMD=2∠BCM2∠DCM
　　　　　　　 　　　　　 =2(∠BCM∠DCM)= 2∠BCD. ……………………………………5分
　　　　　　　 　　　　即 ∠BMD=2∠BCD.
　　　　　　　 证法二：∵ 点M是Rt△BEC的斜边EC的中点，
　　　　　　　 　　　　∴ BM=EC=ME.
　　　　　　　 　　　　又 点M是Rt△DEC的斜边EC的中点，
　　　　　　　 　　　　∴ DM=EC=MC.
　　　　　　　 　　　　∴ BM=DM. ……………………………………………………………3分
　　　　　　　 　　　　∵ BM=ME， DM=MC，
　　　　　　　 　　　　∴ ∠BEC=∠EBM， ∠MCD=∠MDC. …………………………………4分
　　　　　　　 　　　　∴ ∠BEM+∠MCD=∠BAC =90°.
　　　　　　　 　　　　∴ ∠BMD=180°(∠BMC+∠DME)
　　　　　　　 　　　　　 =180°(∠BEM+∠MCD)=180°2(90°∠BCD)=2∠BCD.……………5分
　　　　　　　 　　　　即∠BMD=2∠BCD.
　　　　　　(3)所画图形如图所示：
　　　　　　　　
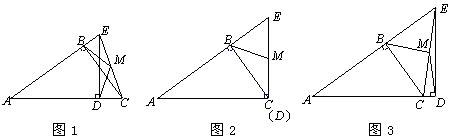
　　　　　　　 图1中有BM=DM，∠BMD=2∠BCD；
　　　　　　　 图2中∠BCD不存在，有BM=DM；
　　　　　　　 图3中有BM=DM，∠BMD=360°2∠BCD.……………………………………………8分
　　说明：每种情况图形及结论正确各1分.

　　25．解：(1)设以为对称轴的抛物线的解析式为，
　　　　　　　 由已知得点C、D的坐标分别为C(2，0)、D(0，-4)，分别代入解析式，
　　　　　　　 得， 解得
　　　　　　　 ∴为所求. ……………………………………………2分
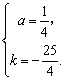
　　　　　　(2)(图1)∵点C(2，0)关于直线的对称点为点B(，0)，
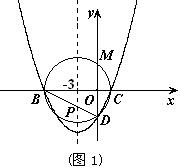
　　　　　　　 ∴要求PC+PD的最小值，即求线段BD的长.
　　　　　　　 在Rt△BOD中，由勾股定理得，
　　　　　　　 ∴PC+PD的最小值是.………………………4分
　　　　　　　 ∵点P是对称轴上的动点，
　　　　　　　 ∴PC+PD无最大值.
　　　　　　　 ∴PC+PD的取值范围是. …………5分
　　　　　　(3)存在.
　　　　　　　 ①(图2)当BC为平行四边形的一边时，
　　　　　　　 　若点F在抛物线上，且使四边形BCFE或四边形BCEF为平行四边形，则有BC∥EF且BC=EF.
　　　　　　　 　设点E(-3，t)，过点E作直线EF∥BC与抛物线交于点F(m，t).
　　　　　　　 　由，得. ∴(7，t)，(-13，t).
　　　　　　　 　又当时，.
　　　　　　　 　∴(7，)，(，). ……………………………………………7分
　　　　　　　 ②(图3)当BC为所求平行四边形的对角线时，
　　　　　　　 　由平行四边形性质可知，点F即为抛物线的顶点(，). ……8分
　　　　　　　 　∴存在三个符合条件的F点，分别为(7，)，(，)，(，).
　　　　　　　　　　　　　　　
　　(说明：各解答题不同的解法参照以上标准给分)