【内容提要】
1、 定义：
把一个图形绕着某一点O转动一个角度的图形变换叫做旋转．点O叫做旋转中心，转动的角叫做旋转角．
注：根据旋转的概念可知,旋转变换包括三个方面的要素，即旋转中心、旋转方向和旋转角度．
2、旋转的性质：
①旋转后的图形与原图形是全等的；
②旋转前后两个图形对应点到旋转中心的距离相等；
③对应点与旋转中心所连线段的夹角都等于旋转角；
3、中心对称
（1）概念：把一个图形绕着某一个点旋转180°，如果它能够与另一个图形重合，那么就关于说这两个
图形关于这个点对称或中心对称，这个点叫做对称中心，这两个图形中的对应点叫做中心的对称点。
（2）性质：中心对称是一种特殊的旋转（旋转角为180°），满足旋转的性质，由旋转的性质可以得到
中心对称性质：
①关于中心对称的两个图形是全等的；
②对称点所连线段经过对称中心；
③对称点所连线段被对称中心平分．
4、平移、旋转、轴对称的区别和联系
学习旋转变换与学习平移、轴对称的过程基本一致，主要都是研究变换过程中的不变量，是研究几何问题、发现几何结论的有效工具. 平移、轴对称、旋转都是全等变换，只改变图形的位置，不改变图形的形状和大小. 由于变换方式的不同，故变换前后具有各自的性质.
| 平移 | 轴对称 | 旋转 | ||
| 相同点 | 都是全等变换，即变换前后的图形全等. | |||
| 不同点 | 定义 | 把一个图形沿某一方向移动一定距离的图形变换，叫~. | 把一个图形沿着某一条直线折叠的图形变换叫~. | 把一个图形绕着某一定点转动一个角度的图形变换叫~. |
| 图形 |  |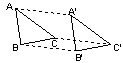
 |
 | |
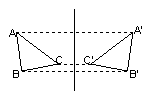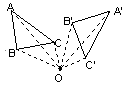要素 |
平移方向 平移距离 |
对称轴 | 旋转中心、旋转方向、 旋转角度 | |
| 性质 | 连接各组对应点的线段平行(或共线)且相等. | 任意一对对应点所连线段被对称轴垂直平分. | 对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角. 即：对应点与旋转中心连线所成的角彼此相等. | |
5、旋转与中心对称
中心对称是一种特殊的旋转(旋转180°)，满足旋转的性质，由旋转的性质可以得到中心对称性质.
| 旋转 | 中心对称 | ||
| 图 形 |
 |
 | |
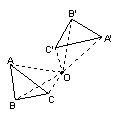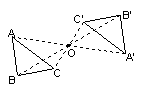| 性质 | 1 | 对应点与旋转中心所连线段的夹角等于旋转角. | 对称点所连线段都经过对称中心. |
| 2 | 对应点到旋转中心的距离相等. | 对称点所连线段被对称中心所平分. | |
| 3 | 旋转前、后的图形全等. | 关于中心对称的两个图形是全等图形 | |
【典型例题】
1、利用旋转的性质确定一个旋转变换的旋转中心、旋转角，探索图形之间的变换关系.
1、如图，在平面直角坐标系中，△ABC和△DEF为等边三角形，AB=DE，点B、C、D在x轴上，点
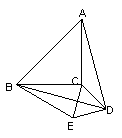
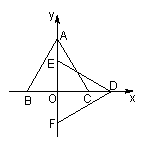A、E、F在y轴上，下面判断正确的是（ ）A．△DEF是△ABC绕点O顺时针旋转90°得到的
B．△DEF是△ABC绕点O逆时针旋转90°得到的
C．△DEF是△ABC绕点O顺时针旋转60°得到的
D．△DEF是△ABC绕点O顺时针旋转120°得到的
解：选A，也可以绕点O逆时针旋转270°。
2、以图1的右边缘所在直线为轴将该图案向右翻折180°后，再按顺时针方向旋转180°，所得到的图形是（ ）
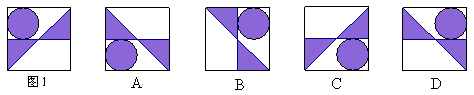
解：选A。
2、利用旋转、中心对称的性质作图.
3、在如图1的方格纸中，每个小方格都是边长为1个单位的正方形，△ABC的三个顶点都在格点上(每个小方格的顶点叫格点).画出△ABC绕点O顺时针旋转90°后的△A1B1C1，并求AA1的长.
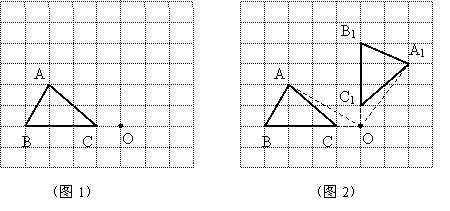
解：如图2，△A1B1C1记为所求，AA1=
。4、已知：如图，试用一条直线把图形分成面积相等的两部分（至少三种方法）.
[分析]利用过中心对称图形的对称中心的直线等分该图形的面积。
解：
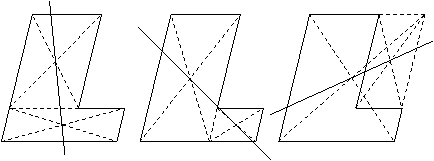
3、运用图形变换的思想解决问题.
5、如图，以等腰直角三角形ABC的斜边AB为边向内作等边△ABD，连结DC，以DC为边作
等边△DCE．B、E在C、D的同侧，若AB＝
，则BE＝____________．解：∵在等边△ABD中，BD=AD，∠ADB=60°，
在等边△CDE中，DE=CD，∠CDE=60°，
∴∠BDE=∠ADC=60°-∠BDC.
∴△BDE≌△ADC.
∴BE=AC
∵在等腰Rt△ABC中，AB=
，∴AC=1，∴BE=1.[小结]我们可以看成把△BDE绕点D顺时针旋转60°，得到△ADC.
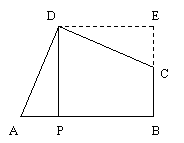
6、如图，在四边形ABCD中，∠ADC=∠ABC=90°， AD=CD，DP⊥AB于P，若四边形ABCD的面积是16，求DP的长.[分析] 根据AD=CD，∠ADC=90°，试想将△APD绕点D逆时针旋转90°，得到△CED，可证四边形DPBE为正方形，但比较麻烦，不如先将四边形DPBC补成一个正方形。
解：过点D作DE⊥BC于点E，
∵DP⊥AB，∴∠DPB=∠DEB=90°，
∵∠ABC=90°，
∴四边形DPBE是矩形，∴∠PDE=90°，即∠CDE+∠CDP=90°
∵∠ADC=∠ADP+∠CDP=90°,
∴∠ADP=∠CDE
∵AD=CD, ∠APD=∠CED=90°,
∴△ADP≌△CDE
∴DP=DE.
∴矩形DPBE是正方形.
∵
，∴DP=4.
7、如图，设P是等边三角形ABC内一点，PB=3，PA=4，PC=5，求∠APB的度数.[分析]要将题目条件中的三条线段尽可能集中在一个三角形中，而且出现等腰（或等边）三角形就可以利用旋转思想来构造全等三角形。
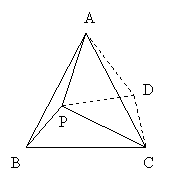解：∵△ABC为等边三角形，∴AB=AC，∠BAC=60°.将△PAB绕点A逆时针旋转60°，得到△DAC，
∴△PAB≌△DAC．
∴PA=AD=4，PB=CD=3，∠APB=∠ADC．
∵在Rt△PCD中，PC=5，
∴
.∴∠PDC=90°．
∵PA=AD，∠PAD=60°，
∴△PAD为等边三角形．
∴∠PDA=60°．
∵∠ADC=∠PDA+∠PDC=150°，
∴∠APB=150°．
8、如图，在四边形ABCD中，∠ABC＝30°，∠ADC＝60°，AD=CD. 求证：BD2=AB2+BC2. 
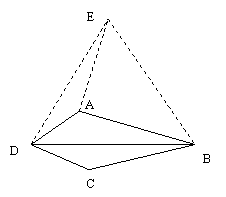[分析]利用AD=CD可以将△BCD绕点D逆时针 旋转60°，从而把条件集中到一个三角形中。证明：∵AD=CD，∠ADC=60°，
∴△BCD绕点D逆时针旋转60°，得到△EAD，
∴∠BDE=∠CDA=60°，△BCD≌△EAD．
∴BC=AE， BD=DE，∠DAE=∠DCB
∴△BDE为等边三角形．
∴BE=BD．
∵在四边形ABCD中，∠ABC＝30°，∠ADC＝60°，
∴∠DCB+∠DAB=270°，即∠DAE+∠DAB=270°．
∴∠BAE=90°．
∵在Rt△BAE中，
，∴
．
