|
二次根式化简和运算
本周内容:二次根式的化简和运算
本周重点、难点:二次根式的化简和运算。
本周重点、难点分析:
1. 最简二次根式
(1) 最简二次根式的概念
我们已经知道,根据二次根式的性质可以把二次根式化简,就是把一个二次根式化成最简单的形式.那么,什么是最简二次根式呢?
满足下列两个条件的二次根式叫最简二次根式.
(1)被开方数的因数是整数,因式是整式;
(2)被开方数中不含能开得尽方的因数或因式.
对应上面两个条件,最简二次根式可以这样理解:
(1)被开方数不含分母;
(2)被开方数中的每一个因式或因数都开不尽方.
 1.下列式子哪些是最简二次根式?哪些不是?为什么? 1.下列式子哪些是最简二次根式?哪些不是?为什么?

分析: 根据最简二次根式的条件来判断,不满足其一个条件的,都不是最简二次根式.
解:
因数;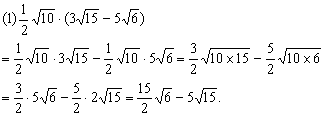 被开方数含有能开得尽方的因数; 被开方数含有能开得尽方的因数; 的被开方数不是整数; 的被开方数不是整数;
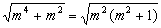 被开方数含有能开得尽方的因式; 被开方数含有能开得尽方的因式;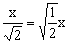 被开方数不是整数. 被开方数不是整数.
(2)将二次根式化为最简二次根式的方法步骤
把一个二次根式化成最简二次根式,有以下两种情况:
(1)如果被开方数是分式或分数(包括小数),先利用商的算术平方根的性质把它写成分式的形式,然后再分母有理化化简.
(2)如果被开方数是整式或整数,先将它分解因式或分解质因数,然后把开得尽方的因式或因数开出来,从而将式子化简.
化二次根式为最简二次根式的步骤:
(1)把被开方数(式)分解质因数(式),化为积的形式;(2)把根号内能开得尽方的因数(或式)移到根号外;(3)化去根号内的分母.若被开方数的因数中有带分数要化成假分数,小数化成分数.
 2.把下列各式化成最简二次根式: 2.把下列各式化成最简二次根式:
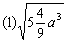 ; ; 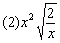
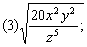 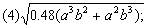
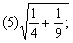 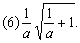
分析: 根据化简二次根式的方法步骤,进行化简.
解法:
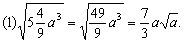
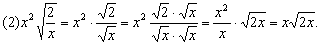
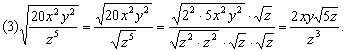
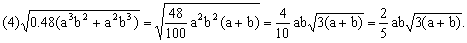

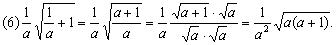
(3)分母有理化时有理化因式的选择
对于分母中含有根号的二次根式,把分母中的根号化去,叫做分母有理化.
根据分式的基本性质,把一个分式的分子、分母同乘以一个不等于零的整式,分式的值不变.因此化去分母中的根号的关键是选择一个适当的数(或代数式),用这个数(或代数式)去乘分式的分子和分母,可以使分母不含根号.如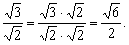
一般地,两个含有二次根式的代数式相乘时,如果它们的积不含二次根式,我们就说这两个代数式互为有理化因式.例如,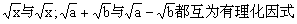
常用有互为有理化因式有以下几种:



注:分母有理化的因式不是惟一的.
 3.把下列各式分母有理化: 3.把下列各式分母有理化:
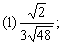 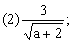
 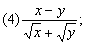

分析: 第(1)题分母是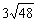 ,先化简,再分母有理化;第(2)题分母 ,先化简,再分母有理化;第(2)题分母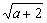 的有理化因式仍是 的有理化因式仍是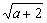 ;第(3)题分母 ;第(3)题分母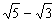 的有理化因式是 的有理化因式是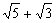 ;第(4)题分子x-y可以分解成 ;第(4)题分子x-y可以分解成 后,直接与分母约分,从而化去分母;第(5)题若直接分母有理化比较麻烦,根据本题特点,分子、分母分别分解因式,然后约分. 后,直接与分母约分,从而化去分母;第(5)题若直接分母有理化比较麻烦,根据本题特点,分子、分母分别分解因式,然后约分.
解:
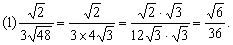


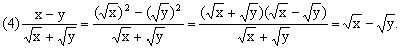

点评: 分母有理化是化简二次根式的一种重要方法.分母有理化时,应结合题目的具体特点,选择适当的方法.如上面第(1)题若使分母、分子都乘以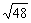 ,虽然可以达到分母有理化的目的,但计算比较繁.所以,当分子、分母中二次根式可以化简时应选将其化简.再如第(4)、(5)两题分子或分母可以分解因式,并且分解后的因式能够约分的,最好不要直接分母有理化. ,虽然可以达到分母有理化的目的,但计算比较繁.所以,当分子、分母中二次根式可以化简时应选将其化简.再如第(4)、(5)两题分子或分母可以分解因式,并且分解后的因式能够约分的,最好不要直接分母有理化.
注: 形如 的式子,分母有理化时,不宜采用分子、分母都乘以 的式子,分母有理化时,不宜采用分子、分母都乘以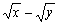 ,因为 ,因为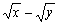 有可能等于零.此题也可以这样解: 有可能等于零.此题也可以这样解:
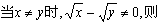
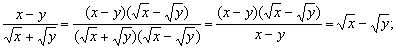
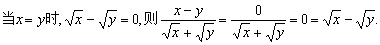
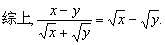
2.二次根式的加减乘除混合运算
(1)二次根式的加减运算
二次根式的加减,首先要化简二次根式,化简之后,就类似整式的加减运算了.整式的加减实质就是去括号和合并同类项.二次根式的加减也是如此.合并同类二次根式与合并同类项类似.如:
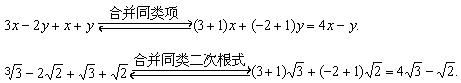
 4.计算: 4.计算:
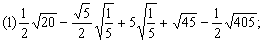


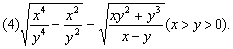
分析: 先化简二次根式,再合并同类二次根式.
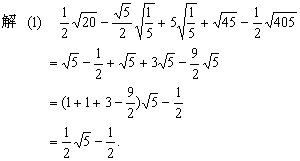
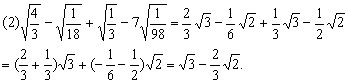
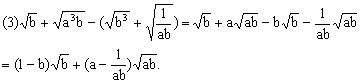
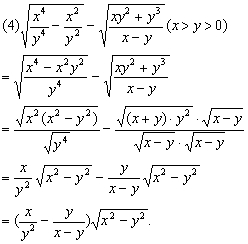
(2)二次根式的混合运算
二次根式的混合运算是本章学习的落脚点,是前面学过的二次根乘法、除法及加减法的综合运用.学习二次根式的混合运算应注意以下几点:
(1)二次根式的混合运算顺序与实数运算类似,先算乘方,再算乘除,最后算加减,有括号先算括号里
面的.
(2)对于二次根式混合运算,原来学过的所有运算律、运算法则及乘法公式仍然适用.
(3)在二次根式混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往
往能事半功倍.
 5.计算: 5.计算:

分析:这里可以把二次根式看成是一个“单项式”或者“多项式”利用整式乘法或除法法则进行运算.
解:
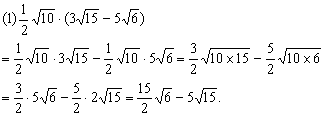
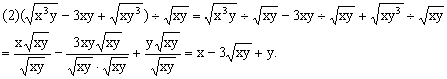


点评 第(1)、(2)、(3)题都与整式运算类似.第(4)题,因为除法不满足分配律,可先转化成分数形式,再分母有理化.
 6.计算: 6.计算:
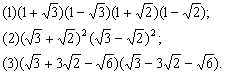
分析:这三道题都可以利用平方差公式或完全平方公式.
解:

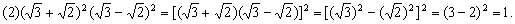

|