|
梯 形
知识要点:
1.梯形的定义:
一组对边平行而另一组对边不平行的四边形叫做梯形.
说明:(1)梯形是一种特殊的四边形;
(2)证明梯形时除了证明一组对边平行外,特别注意还要证明另一组对边不平行;
有时证明不平行比较困难,还可以证明平行的这一组对边不相等.
2.梯形常用的辅助线做法:
(1) 过一顶点作一腰的平行线,分解成一个平行四边形和一个三角形;
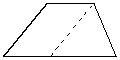
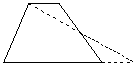
(2) 过一顶点作一条对角线的平行线,构造出平行四边形和一个面积与梯形相等的三角形;
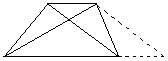 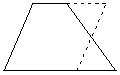
(3) 过一腰中点作另一腰的平行线,构造出平行四边形和一对全等的三角形;
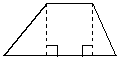
(4) 过一底边的端点作另一底边的垂线, 构造出一个矩形和两个直角三角形;特别对于等腰梯形,两
个直角三角形全等;
(5) 延长梯形的两腰使其交于一点, 构成两个形状相同的三角形;
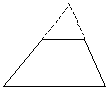
(6) 连接一顶点和一腰的中点并延长与底边相交,构造一对全等的三角形, 将梯形作等积变换;
3.特殊的梯形
1)等腰梯形:两腰相等的梯形叫做等腰梯形.
性质:(1)等腰梯形的同一底边上的两个角相等;等腰梯形的两条对角线相等.
(2)同一底边上的两个角相等的梯形是等腰梯形.
(3)等腰梯形是轴对称图形,它的对称轴是经过两底中点的一条直线.
2)直角梯形:有一个角是直角的梯形叫做直角梯形.
例题分析
 1.已知:如图,四边形ABCD为矩形,四边形ABDE为等腰梯形, 1.已知:如图,四边形ABCD为矩形,四边形ABDE为等腰梯形,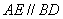 。 。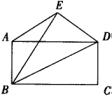
求证: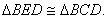
证明:∵四边形ABCD为矩形,∴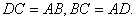
∵四边形ABDE为等腰梯形,且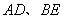 为其对角线, 为其对角线,
∴ 。在 。在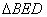 和 和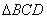 中, 中,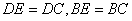 , ,
又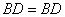 ,∴ ,∴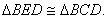
 2.已知,如图,梯形ABCD中, 2.已知,如图,梯形ABCD中,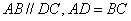 ,延长AB到E,使 ,延长AB到E,使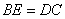 , ,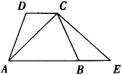
求证: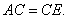
证法一:由四边形ABCD是等腰梯形,∴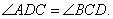
又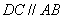 ,∴ ,∴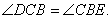
∴∠ADC=∠CBE
在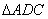 与 与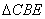 中, 中,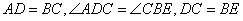 , ,
于是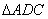 ≌ ≌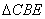 ,故 ,故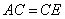 。 。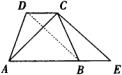
证法二:如图,连结BD,由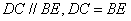 可知四边形DCEB为平行四边形, 可知四边形DCEB为平行四边形,
所以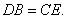
又四边形ABCD为等腰梯形,于是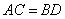 ,故 ,故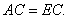
证法三:如图,作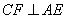 于 于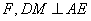 于M。 于M。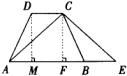
在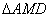 与 与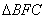 中, 中,
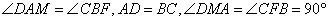 , ,
所以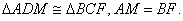
又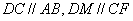 ,故 ,故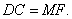
又由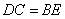 ,可得MF=BE ,可得MF=BE
所以
所以F为AE的中点,CF为AE的垂直平分线,所以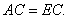 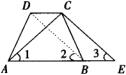
证法四:如图,连结BD。
由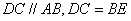 知四边形BECD为平行四边形,所以 知四边形BECD为平行四边形,所以 。 。
又四边形ABCD是等腰梯形,所以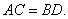
又由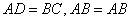 ,可知 ,可知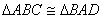 。 。
所以∠1=∠2
所以∠1=∠3
所以AC=CE
说明:本题采用了几种常用的作辅助线的方法证得结论,目的是说明解与梯形有关的问题经常用这些作辅助线的方法。
 3.如图,把边长为2cm的正方形剪成四个全等的直角三角形.请用这四个直角三角形拼 3.如图,把边长为2cm的正方形剪成四个全等的直角三角形.请用这四个直角三角形拼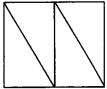 成符合下列要求的图形(全部用上,互不重叠且不留空隙),并把你的拼法画出来: 成符合下列要求的图形(全部用上,互不重叠且不留空隙),并把你的拼法画出来:
(1)不是正方形的菱形一个;
(2)不是正方形的矩形一个;
(3)梯形两个;
(4)不是矩形、菱形的平行四边形一个;
(5)不是梯形和平行四边形的凸四边形一个。
解: 
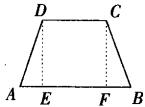  4.如图,已知:四边形ABCD是等腰梯形,其中 4.如图,已知:四边形ABCD是等腰梯形,其中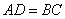 ,若 ,若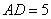 , ,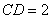 , ,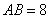 . .
求:梯形ABCD的面积.
解答:过点D、C作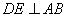 于E, 于E,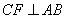 于F. 于F.
则根据等腰梯形的轴对称性可知: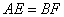 . .
∵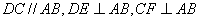 , ,
∴四边形CDEF是矩形.
∴ 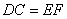 . .
∴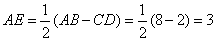
在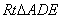 中,根据勾股定理有, 中,根据勾股定理有,
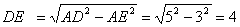
∴ 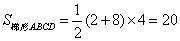 . .
 5.如图,已知:在梯形ABCD中, 5.如图,已知:在梯形ABCD中, ,AC、BD相交于点O. ,AC、BD相交于点O. 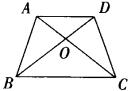
求证: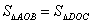 . .
证明:∵ , ,
∴A、D两点到BC的距离相等.
即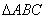 中BC边上的高与 中BC边上的高与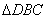 中BC边上的高相等. 中BC边上的高相等.
∴ 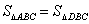 (等底等高). (等底等高).
∴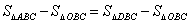
∴ 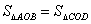
 6.已知梯形ABCD中,AD∥BC,AD=5cm.BC=7cm,AB=6cm 6.已知梯形ABCD中,AD∥BC,AD=5cm.BC=7cm,AB=6cm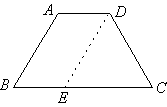
求另一腰CD的取值范围.
解:如图,过D点作DE∥AB,交BC于点E .
∵AD∥BC,DE∥AB,
∴四边形ABED是平行四边形,
∴DE=AB=6,
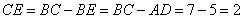 . .
在△DEC中,
∵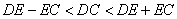 , ,
∴4(cm)< DC < 8(cm).
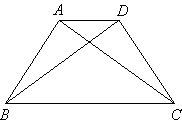
 7.如图,已知:在等腰梯形ABCD中, 7.如图,已知:在等腰梯形ABCD中,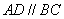 . .
(1)若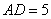 , ,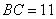 ,梯形的高是4,求梯形的周长; ,梯形的高是4,求梯形的周长;
(2)若 , ,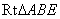 ,梯形的高是 ,梯形的高是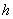 ,求梯形的周长 ,求梯形的周长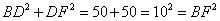 ; ;
(3)若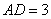 , , , ,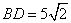 ,求证: ,求证: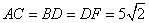 . .
解:(1)如图,过点A作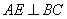 于点 于点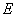 , ,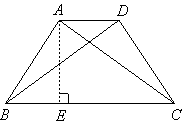
则在等腰梯形ABCD中,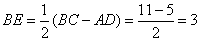 . .
在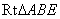 中, 中,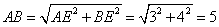 . .
所以,等腰梯形ABCD的周长是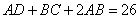 . .
(2)类似(1),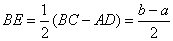 . .
在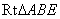 中, 中,
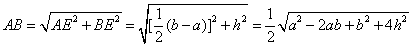 . .
所以,等腰梯形ABCD的周长是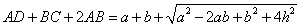 . .
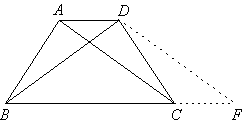 (3)如图,过点D作 (3)如图,过点D作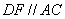 ,交BC的延长线于点F, ,交BC的延长线于点F,
即得平行四边形ACFD,
则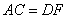 , ,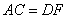 . .
在等腰梯形ABCD中,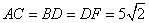 . .
而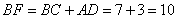 . .
在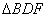 中, 中,
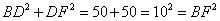 . .
所以∠BDF=90°,即BD⊥DF
又因为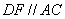
所以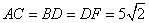
 8.如图,在梯形ABCD中,对角线 8.如图,在梯形ABCD中,对角线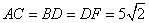 于点P. 于点P.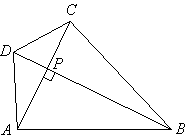
求证: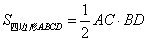 . .
证明:由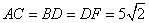 ,可知 ,可知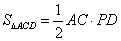 , ,
且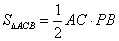 . .
所以,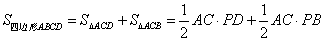
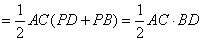 . .
解答问题:
(1)上述证明得到的性质可以叙述为:___________________.
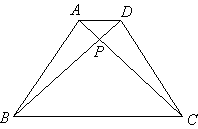 (2)已知:如图,等腰梯形ABCD中, (2)已知:如图,等腰梯形ABCD中,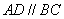 ,对角线 ,对角线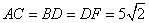 于点P, 于点P,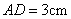 , ,
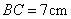 ,利用上述的性质求梯形的面积. ,利用上述的性质求梯形的面积.
解析:
(1)对角线互相垂直的四边形的面积等于对角线乘积的一半.
(2)先利用例7(3)的方法,求出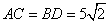 ; ;
再利用上述性质,求出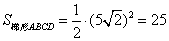 . .
 9.已知:梯形ABCD中,AD∥BC,E为DC中点,EF⊥AB于F点,AB=3cm,EF=5cm, 9.已知:梯形ABCD中,AD∥BC,E为DC中点,EF⊥AB于F点,AB=3cm,EF=5cm,
求梯形ABCD的面积.
解:如图,过E点作MN∥AB,分别交AD的延长线于M点,交BC于N点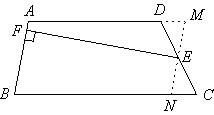 . .
∵DE=EC,AD∥BC,
可以证明△DEM ≌△CNE,
四边形ABNM是平行四边形.
∵EF⊥AB,
∴S梯形ABCD=S□ABNM=AB×EF=3cm×5cm=15cm2.
 10.已知:梯形ABCD中, AD=1,BC=4,BD=3,AC=4,求梯形ABCD的面 10.已知:梯形ABCD中, AD=1,BC=4,BD=3,AC=4,求梯形ABCD的面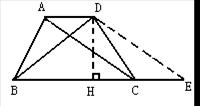 积。 积。
解:如图,作DE∥AC,交BC的延长线于E点。
∵AD∥BC
∴四边形ACED是平行四边形
∴BE=BC+CE=BC+AD=4+1=5
DE=AC=4
在△DBE中,∵BD=3,DE=4,BE=5
∴∠BDE=90°
作DH⊥BC于H,则
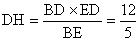
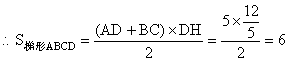
 11.已知:梯形ABCD中,AD∥BC,E是AB的中点,△ECD的面积为10, 11.已知:梯形ABCD中,AD∥BC,E是AB的中点,△ECD的面积为10,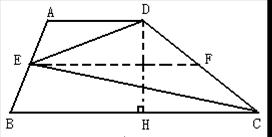
求梯形ABCD的面积。
解:如图12,取DC的中点F,连结EF,
作DH⊥BC于H点。
∵AE=EB,DF=FC,AD∥BC,
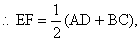 EF∥AD∥BC,DH⊥EF EF∥AD∥BC,DH⊥EF
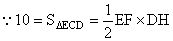
∴EF×DH=20
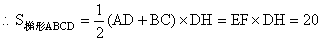
 12.有一块梯形形状的土地,现要平均分给两个农户种植(即将梯形的面积两等分),试设计两种方案(平分方案画在备用图上),并给予合理的解释. 12.有一块梯形形状的土地,现要平均分给两个农户种植(即将梯形的面积两等分),试设计两种方案(平分方案画在备用图上),并给予合理的解释.
图(1) 图(2)
分析:思路(一) 连接梯形上、下底的中点.
思路(二) 在下底上截一边及另一腰为边的三角形,使它们面积为原梯形面积的一半.
思路(三) 取梯形一条对角线的中点,连接另外两个顶点所得的两个四边形.
解:设梯形上、下底分别为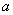 、 、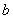 ,高为 ,高为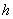 . .
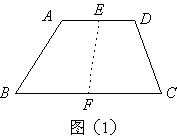
方案一:如图(1),连接梯形的上、下底的中点E、F,则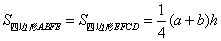 . .
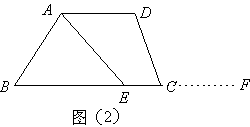
方案二:如图(2),延长BC至F,使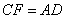 ,取 ,取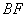 的中点E,连接AE, 的中点E,连接AE,
则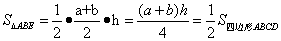 . .
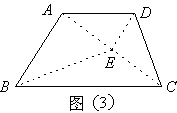
方案三:如图(3),连接AC,取AC的中点E,连接BE、ED,
则四边形ABED的面积等于梯形ABCD的面积的一半.分析可知,
因为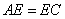 ,所以 ,所以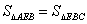 , ,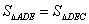 , ,
所以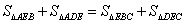 , ,
故有四边形ABED的面积等于梯形ABCD的面积的一半.
|