菱形的性质与判定
本周目标:
　　掌握菱形的定义，了解菱形与平行四边形的关系；掌握菱形的性质与判定；能运用菱形性质与判定解决相关问题；通过实际应用提高学生用数学的意识。

重点:
　　本周教学的重点是菱形的性质及判定

难点：
　　区别菱形的性质与判定并正确运用其解决相关问题。

知识要点：
1、 菱形的定义：
　　有一组邻边相等的平行四边形叫菱形。
　　　

2、菱形的性质：
　　性质1　菱形的四条边相等。
　　性质2　菱形的对角线互相垂直并且每一条对角线平分一组对角。
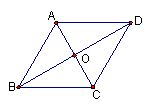
　　已知：菱形ABCD中，对角线AC和BD相交于点O（如图1）
　　求证：AC⊥BD，AC平分∠BAD和∠BCD，BD平分∠ABC和∠ADC。
　　证明：∵四边形ABCD是菱形
　　　　　∴AB＝AD（菱形的四条边相等）
　　　　　在等腰△ABD中，∵BO＝OD，
　　　　　∴AC⊥BD，AC平分∠BAD。
　　　　　同理：
　　　　　AC平分∠BCD；BD平分∠ABC和∠ADC。
　　　　　　　　　　　
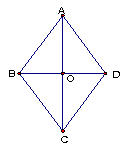
　　　　　　　　　　　　　　　图1

3、菱形面积计算方法：
　　(1) S＝底×高
　　(2) S＝对角线1×对角线2＝ab
　　例　已知菱形ABCD的边长为2cm ，∠BAD＝120°，对角线AC、BD相交于点O（如下图），求这个菱形的对角线长和面积。
　　解：∵四边形ABCD是菱形
　　　　　
　　　　∴AC⊥BD，∠BAO＝＝×120°＝60°
　　　　（菱形的对角线互相垂直，并且每一条对角线平分一组对角）
　　　　在Rt△AOB中，
　　　　∵∠ABO＝90°－∠BAO＝30°
　　　　∴AO＝＝×2＝1（cm）
　　　　BO＝（cm）
　　　　∵AO＝，BO＝
　　　　∴AC＝2AO＝2（cm），BD＝2BO＝2（cm）
　　　　∴S_菱形ABCD＝AC×BD＝2（cm²）

4、菱形的判定：
　　判定定理1　四边都相等的四边形是菱形。
　　判定定理2　对角线互相垂直的平行四边形是菱形。

本周典型例题分析：
　　1．已知：如图，□ABCD中，AB=2BC，E、F是直线BC上的点，BE=BC=CF，求证：AF⊥ED
　　分析：若连结MN，欲证DE⊥AF，只要证四边形AMND是菱形。
　　证明：连结MN
　　　　　∵四边形ABCD是平行四边形
　　　　　∴ADBC，ABDC
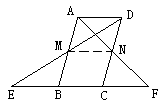　　　　　在△ABF中，∵BC=CF，AB∥CN
　　　　　∴AN=NF
　　　　　又∵AD∥BF，∴DN=NC
　　　　　同理可证：AM=MB
　　　　　又∵AB=2BC
　　　　　∴AMDN，
　　　　　∴四边形AMND是平行四边形
　　　　　而AD=DN，∴四边形AMND是菱形
　　　　　∴AN⊥MD，即AF⊥ED
　　换个思路想一想，如果利用“如果一个三角形的一边上的中线等于这边的一半，那么这条边所对的角是直角。”这个直角三角形的判定定理 ,如何证？
　　解法2：如图，延长BE至G，使得EG=EB，连结AG
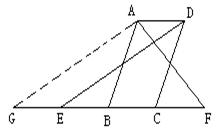
　　　　　 ∵AB=2BC，EB=BC=CF
　　　　　 ∴在△AGF中，AB=GB=FB
　　　　　 ∴∠GAF=90°，即GA⊥AF
　　　　　 ∵四边形ABCD是平行四边形
　　　　　 ∴ADBC
　　　　　 又∵GE=BC，∴GEAD
　　　　　 ∴四边形AGED是平行四边形
　　　　　 ∴AG∥ED，
　　　　　 ∴AF⊥ED
　　想一想，例1还有哪些证法？

　　2. 已知：如图，Rt△ABC中，CD⊥AB于D，∠ACB=90°，AF平分∠BAC，交CD于E，FG⊥AB于G，求证：四边形GFCE是菱形
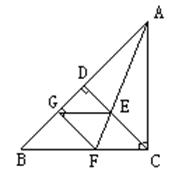　　分析：可先证四边形GFCE是平行四边形，再证它是菱形
　　证明：如图所示，
　　　　　∵AF平分∠BAC，FG⊥AB、FC⊥AC，
　　　　　∴FG=FC
　　　　　在△ABC中，∵∠ACB=90°，CD⊥AB，
　　　　　∴∠B=∠ACD
　　　　　∴∠CEF=∠CAF+∠ACD=∠BAF+∠B=∠EFC
　　　　　在△CEF中，∵∠CEF=∠CFE，∴CE=CF
　　　　　又∵CD⊥AB，FG⊥AB
　　　　　∴CEFG
　　　　　∴四边形CEGF是平行四边形
　　　　　又∵CE=CF
　　　　　∴四边形CEGF是菱形
　　
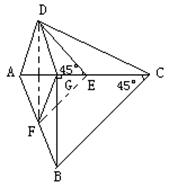　　3. 已知：如图，四边形ABCD中，∠ADC=90°，AC=CB，E、F分别是AC、AB的中点，∠DEA=∠ACB=45°，BG⊥AE于G点。求证：
　　(1)四边形AFGD是菱形；
　　(2)若AC=BC=10cm，求菱形AFGD的面积。
　　证明提示：
　　①在Rt△ABG中，由F是斜边AB的中点，可得AF=GF
　　②在△ABC中，若连结EF，由E、F分别是AC、AB的中点，得EFBC，
　　　而由已知，AC=CB，，则DE=EF，
　　　由EF∥BC，则∠AEF=∠ACB=45°
　　③连结DF，由DE=FE，AE平分∠DEF，则AE垂直平分DF，从而AD=AF，GD=GF
　　④由AF=FG=GD=DA，得四边形AFGD为菱形
　　(2)解法提示：
　　①
　　②
　　③

　　4．请阅读下列材料：
　　问题：如图1，在菱形和菱形中，点在同一条直线上，是线段的中点，连结．若，探究与的位置关系及的值．
　　小聪同学的思路是：延长交于点，构造全等三角形，经过推理使问题得到解决．
　　　　　　　　　
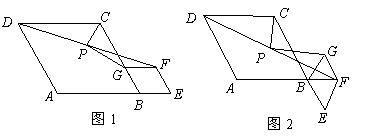
　　请你参考小聪同学的思路，探究并解决下列问题：
　　（1）写出上面问题中线段与的位置关系及的值；
　　（2）将图1中的菱形绕点顺时针旋转，使菱形的对角线恰好与菱形的边
　　　　 在同一条直线上，原问题中的其他条件不变（如图2）．你在（1）中得到的两个结论是否发生
　　　　 变化？写出你的猜想并加以证明．
　　解：（1）线段与的位置关系是；．
　　　　（2）猜想：（1）中的结论没有发生变化．
　　证明：如图，延长交于点，连结．
　　　　　是线段的中点，
　　　　　．
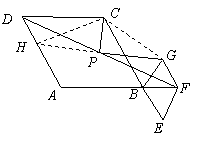
　　　　　由题意可知．
　　　　　．
　　　　　，
　　　　　．
　　　　　，．
　　　　　四边形是菱形，
　　　　　，．
　　　　　由，
　　　　　且菱形的对角线恰好与菱形的边在同一条直线上，
　　　　　可得．
　　　　　．
　　　　　四边形是菱形，
　　　　　．
　　　　　．
　　　　　．
　　　　　，．
　　　　　．
　　　　　即．
　　　　　，，
　　　　　，．
　　　　　．

　　5. 已知：如图，由菱形ABCD的顶点C作CF⊥射线AD于F点，CE⊥射线AB于E点，试确定CF与CE的大小关系，并证明你的结论。
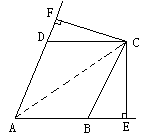　　分析与提示：对于提出的猜想CF=CE，许多同学采取证明△CFD≌△CEB，但是此方法显然不如“连结AC”这个证法好。
　　解：CF=CE证明如下，连结AC
　　　　∵四边形ABCD是菱形，
　　　　∴∠CAE=∠CAF
　　　　又∵CE⊥AE，CF⊥AF，∴CF=CE

　　6. 已知：如图，E是菱形ABCD边AD的中点，EF⊥AC于H，交CB的延长线于F点，交AB于G点。
　　求证：AB与EF互相平行分于G点
　　分析：欲证AB与EF互相平分于G点，连结AF、EB，只要证四边形AFBE是平行四边形，又需证AEFB，为此，就要考虑E是AD边中点及EF⊥AC的条件如何运用。
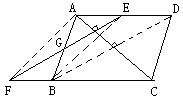　　证明：如图，分别连结AF、BE、BD
　　　　　∵四边形ABCD是菱形
　　　　　∴AD∥BC，AC⊥BD
　　　　　又∵EF⊥AC，∴EF∥BD
　　　　　∵EF∥BD，ED∥FB
　　　　　∴四边形EFBD是平行四边形
　　　　　∴EDFB
　　　　　又∵AE=ED,∴AEFB
　　　　　∴四边形AFBE是平行四边形
　　　　　∴AB、EF互相平分于G点