本周目标：
1．掌握平行四边形的概念及性质，会应用性质解决简单的几何问题；
2．掌握平行四边形的五种判定方法，会应用判定方法解决有关问题；
重点：
掌握平行四边形的性质及判定方法，发展逻辑思维能力
难点：
灵活运用平行四边形的性质及判定方法解决几何问题
知识要点：
1．定义：
有两组对边分别平行的四边形叫做平行四边形，平行四边形ABCD，记作“□ABCD”
2．平行四边形的性质：
(1)平行四边形的两组对边分别平行且相等。
(2)平行四边形的两组对角分别相等。
(3)平行四边形的对角线互相平分。
(4)平行四边形是中心对称图形，对称中心是其两条对角线的交点。
(5)平行四边形的面积等于底×高，且两条对角线分平行四边形所成四个小三角形面积相等。
推论：夹在两条平行线间的平行线段相等。
3．平行线间的距离：
两平行线中，一条直线上任意一点到另一条直线的距离叫两条平行线间的距离。
4．平行四边形的判定：
(1)两组对边分别平行的四边形是平行四边形
(2)两组对边分别相等的四边形是平行四边形
(3)两组对角分别相等的四边形是平行四边形
(4)对角线互相平分的四边形是平行四边形
(5)一组对边平行且相等的四边形是平行四边形
例题分析：
1．已知：如图l，□ABCD的对角线AC、BD相交于点O，EF过点O与AB、CD分别相交于点E、F，求证：OE=OF。
证明：∵ 四边形ABCD是平行四边形 ∴ OA=OC，AB∥CD
∴ ∠OAE=∠OCF，∠OEA=∠OFC
∴ △OAE≌△OCF ∴ OE=OF
变形题：已知：如图2，□ABCD的对角线AC、BD相交于点O，EF过点O与DA,BC延长线分别相交于点E、F，求证：OE=OF。
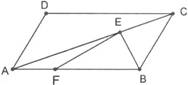
2．已知：□ABCD中，E在AC上，AE=2EC，F在AB上，BF=2AF，若△BEF的面积为2，求：□ABCD的面积。解：∵ △BEF的面积为2且BF=2AF，
∴ S△AEF=
S△BEF =1∴ S△BAE=3
∵ AE=2EC
∴ S△BCE =
S△BAE =1.5∴ S△ABC =4.5
∴ S□ABCD =2S△ABC =9
3．如图，E、F分别是□ABCD边AD和BC上的点，并且AE=CF，AF和BE相交于G，CE和DF相交于H，求证：EF和GH互相平分。
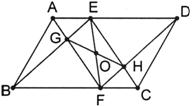
证明：∵ □ABCD ∴AD∥BC AD=BC
∵ AE=CF
∴ □AFCE
∴ AF∥CE
同理： BE∥DF
∴ □EGFH
∴ EF和GH互相平分。
4．如图，□ABCD的周长为
，BC的长为
，AE⊥BC ,AF⊥DC的延长线于F，AE=3，求（1）∠D的度数；（2）AF的长。
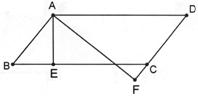
解：∵ □ABCD如图所示，
∴ AB=CD , ∠B=∠D
∵□ABCD的周长为
，BC的长为∴
，∵ AE⊥BC，AF⊥CD AE=3，
∴ BE=3，∴ ∠B=∠D=45°，
∵ AE·BC=AF·CD
∴
，∴
。5．如图，□ABCD中，E、F分别是AD、BC的中点，直线CE交BA的延长线于G，直线DF交AB的延长线于H，CG与DH交于点O，若
，求
。
解答与提示：连结EF，则□ABFE的面积=□CDEF的面积=2
易证
易证△CDE≌△GAE，△CDF≌△BHF；
总结：平行四边形的面积等于底与高的乘积，且它的两条对角线分原平行四边形为四个等积三角形．证明面积关系问题的常用思路有：利用同底(等底)同高(等高)的两个三角形面积相等；利用同一个平行四边形面积找等量关系，也就是用不同关系式表示同一个平行四边形面积找等量关系．
6．已知，如图，在□ABCD中，AE⊥BD，CF⊥BD，M、N分别是BC、AD的中点，求证：四边形EMFN是平行四边形。
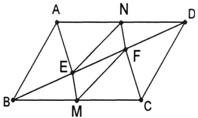
证明：如图示，连结MN交BD于O
∵ □ABCD
∴ AD=BC，AD∥BC
∴ ∠ADB=∠CBD
∵ M、N分别是BC、AD的中点
∴ ND=BM
∵ ∠MOB=∠NOD
△MOB≌△NOD
∴ OM=ON OB=OD
∵ AE⊥BD，CF⊥BD
∴ ∠AED=∠CFB=90°
∴ △AED≌△CFB
∴ DE=BF
∴ OE=OF
∴ 四边形EMFN是平行四边形
7．在□ABCD中，∠A的平分线分BC成4cm和3cm两部分，求□ABCD的
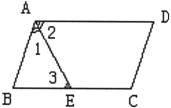周长。分析：此题利用平行四边形的定义：去求BC相邻的边AB的长。
需要注意的是，两部分中，哪一部分是4cm，需讨论。
解：如图，∵ 四边形ABCD是平行四边形
∴ AD∥BC
∴ ∠2=∠3
∵ AE平分∠BAD
∴ ∠1=∠2，∴ ∠1=∠3，
∴ BA=BE
若BE=4cm，则□ABCD的周长=2(AB+BC)=22cm
若BE=3cm，则□ABCD的周长=20cm
8．如图，□ABCD中，BE平分∠ABC，交AD于E，DF平分∠ADC，交BC于F，求证：BF=DE
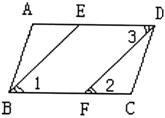
分析：此题证法较多，可以证明△ABE≌△CDF或证明四边形BEDF是平行四边形。
证明：∵ □ABCD中AD∥BC，∠ABC=∠ADC
∴ ∠2=∠3
∵ BE平分∠ABC，DF平分∠ADC
∴
，
∴ ∠1=∠3
∴ ∠1=∠2
∴ BE∥DF
又∵ DE∥BF
∴ 四边形BEDF是平行四边形
∴ BF=DE
9．如图，□ABCD中，2AB=AD，AB=AE=BF，求证：CE⊥DF分析：主要运用平行四边形的性质，要证垂直关系，需证角是90°。
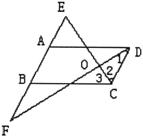
证明：∵□ABCD中，AB∥CD，AD=BC，AD∥BC
∴ ∠2=∠E，∠ADC+∠BCD=180°
∵ AD=2AB，AB=AE
∴ BC=BE
∴ ∠3=∠E，
∴
同理
∴ ∠COD=90°
∴ CE⊥DF
10．如图：□ABCD中，A1，A2，A3，A4和B1，B2，B3，B4分别是AB和CD的五等分点，C1，C2和D1，D2分别是AD和BC的三等分点，若四边形A4C1B1D2的面积为1，求□ABCD的面积。
分析：采用割补求面积，利用平行四边形的性质，建立方程
设□ABCD的面积为x，
由平行四边形的性质，易证：△DC1B1≌△BD2A4，△AA4C1≌△CB1D2
且
∴
∴
.
