要点分析
我们在研究、解决几何问题时,常常把多边形和圆的问题转化为三角形(特别是直角三角形)来解决.然而有些图形结构中无法找到可解的三角形,这时我们就需要将已知的三角形进行平移、旋转或轴对称变换,从而将一些分散的元素(线段或角)重新组合成新的三角形,在新的图形结构中寻求元素之间的关系.这个转化过程就是几何变换的过程.
经典例题
一、用旋转变换分析解决问题
已知:在Rt△ABC中,AB=BC,在Rt△ADE中,AD=DE,连结EC,取EC的中点M,连结DM和BM.
(1)若点D在边AC上,点E在边AB上,且与点B不重合,如图①,探索BM、DM的关系并给予证明;
(2)如果将图①中的△ADE绕点A逆时针旋转小于45°的角,如图②,那么(1)中的结论是否仍成立?
如果不成立,请举出反例;如果成立,请给予证明.
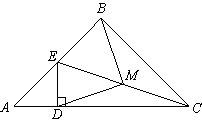
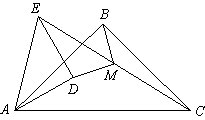
图① 图②
解析:(1)根据“直角三角形斜边的中线等于斜边的一半”,
不难证明
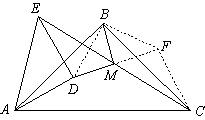
(2)如图,作
连接BD、BF.
则
可得
相当于将
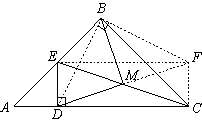
可得
反思一下:由于本题的第(1)问探究的两条线段在特殊位置关系下的数量关系和位置关系,因此证明起来并不困难.而第(2)问探究的两条线段在一般位置关系下的关系,我们以旋转的观点可以清楚地看出这两条线段在运动变化过程中的不变关系.那么第(1)问中的情况是否也符合这个一般规律呢?我们可以用第(2)问中的旋转方法再来研究第(1)问中的特殊情况(如图所示).
二、用平移变换分析解决问题
已知:如图,在平面直角坐标系xOy中,直线
(1)直接写出点C的坐标,并求过A、B、C三点的抛物线的解析式;
(2)若抛物线的顶点为D,在直线BC上是否存在点P,使得四边形 ODAP为平行四边形?若存在,求出点
P的坐标;若不存在,说明理由;
(3)设抛物线的对称轴与直线BC的交点为T,Q为线段BT上一点,直接写出

解析:(1)易求C
过A、B、C三点的抛物线的解析式为
(2)可得抛物线的对称轴为
顶点D的坐标为
设抛物线的对称轴与x轴的交点为G.
直线BC的解析式为
可设点P的坐标为
解法一:如图1,作OP∥AD交直线BC于点P,
连结AP,作PM⊥x轴于点M.
∵ OP∥AD,
∴ ∠POM=∠GAD,tan∠POM=tan∠GAD.
∴
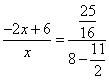 .
.解得
此时点P的坐标为
但此时
∵
∴ OP<AD,即四边形的对边OP与AD平行但不相等,
∴ 直线BC上不存在符合条件的点P.
解法二:如图2,取OA的中点E,作点D关于点E的对称点P,作PN⊥x轴于点N.
则∠PEO=∠DEA,PE=DE.可得△PEN≌△DEG .

由
NE=EG=
∴ 点P的坐标为
∵ x=
∴ 点P不在直线BC上.
∴ 直线BC上不存在符合条件的点P .
用平移变换的想法解题:
解法三:如图2,点D向上平移
再向右平移2.5个单位长度得到点A.
若四边形ODAP为平行四边形,则需要点O向上平移
再向右平移2.5个单位长度得到点P.

而此时点P坐标为(
它不在抛物线
因此不存在符合条件的点P.
(3)
说明:如图3,由对称性可知QO=QH,
反思一下:第(2)问中探究平行四边形的存在性,可以直接根据平行四边形的判定方法解题.显然根据角的关系判定或根据边的关系判定计算量比较大.因此,我们考虑变换一下判定的方法,即OP和AD平行且相等看成D到A和O到P各自平移的方向和长度是相同的.这样,解题的过程就变得容易多了.
三、用轴对称变换分析解决问题
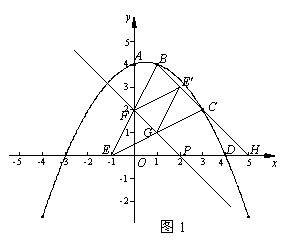
已知抛物线经过点 A(0,4)、B(1,4)、C(3,2),与x轴正半轴交于点D.
(1)求此抛物线的解析式及点D的坐标;
(2)在x轴上求一点E,使得△BCE是以BC为底边的等腰三角形;
(3)在(2)的条件下,过线段ED上动点P作直线PF//BC,与BE、CE分别交于点F、G,将△EFG沿FG翻折得
到△E′FG.设P(x,0),△E′FG与四边形FGCB重叠部分的面积为S,求S与x的函数关系式及自变量
x的取值范围.
 解:(1)抛物线的解析式为
解:(1)抛物线的解析式为(2)点E(
(3)可求得直线BC的解析式为
从而直线BC与x轴的交点为H(5,0).
如图1,根据轴对称性可知S△E ′FG=S△EFG,
当点E′在BC上时,点F是BE的中点.
∵ FG//BC,
∴ △EFP∽△EBH.
可证 EP=PH.
∵ E(-1,0), H(5,0),
∴ P(2,0).
(i) 如图2,分别过点B、C作BK⊥ED于K,CJ⊥ED于J,
则
当-1<x≤2时,
∵ PF//BC,
∴ △EGP∽△ECH,△EFG∽△EBC.
∴
∵ P(x,0), E(-1,0), H(5,0),
∴ EP=x+1,EH=6.
∴
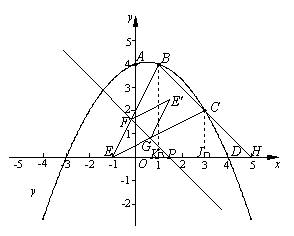
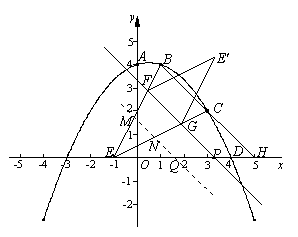
图2 图3
(ii) 如图3,当2<x ≤4时, 在x轴上截取一点Q, 使得PQ=HP,
过点Q作QM//FG, 分别交EB、EC于M、N.
可证S=S四边形MNGF,△ENQ∽△ECH,△EMN∽△EBC.
∴
∵ P(x,0),E(-1,0),H(5,0),
∴ EH=6,PQ=PH=5-x,EP=x+1,
EQ=6-2(5-x)=2x-4.
∴
同(i)可得
∴
综上,
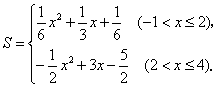
反思一下:本题第(3)问是一个轴对称变换的问题,在图3的情况中直接求重叠部分的面积是比较困难的,我们作一个BC关于FG的对称图形,得到梯形MNGF,它的的面积就容易求得了.
我们希望每一位同学在解综合题后,都能及时进行总结和反思,掌握几何变换的基本方法和一般规律,力求在变化中解决千变万化的数学综合题.
巩固练习
1.在等边
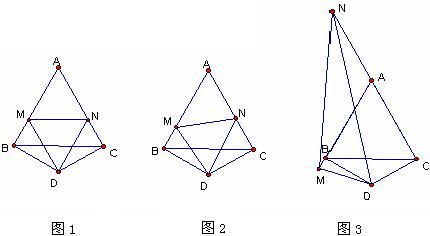
(I)如图1,当点M、N在边分别AB、AC上,且DM=DN时,BM、NC、MN之间的数量关系是____________;
此时
(II)如图2,点M、N分别在边AB、AC上,且当DM
想并加以证明;
(III)如图3,当M、N分别在边AB、CA的延长线上时,若AN=
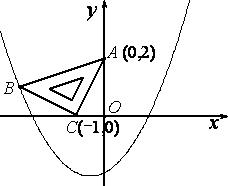 2.在平面直角坐标系中,现将一块等腰直角三角板ABC放在第二象限,斜靠在两坐标轴上,且点A(0,2),点C(-1,0),如图所示,抛物线
2.在平面直角坐标系中,现将一块等腰直角三角板ABC放在第二象限,斜靠在两坐标轴上,且点A(0,2),点C(-1,0),如图所示,抛物线(1)求点B的坐标;
(2)求抛物线的解析式;
(3)在抛物线上是否还存在点P(点B除外),使△ACP仍然是以
AC为直角边的等腰直角三角形?若存在,求所有点P的坐
标;若不存在,请说明理由.
参考答案:
1.(I)BM、NC、MN之间的数量关系BM+NC=MN.此时
(II)结论仍然成立.
设
设
欲求
如图,作
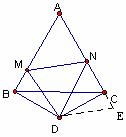
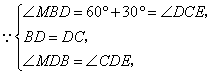

(III)设
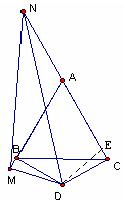
作
不难证明
2.解:不难求得
(1)点B的坐标为(
(2)抛物线解析式为
(3)方法一:①若以AC为直角边,点C为直角顶点;
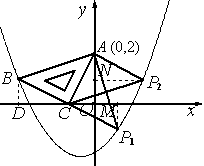 则可以设直线BC交抛物线
则可以设直线BC交抛物线由题意,
直线BC的解析式为:
不难求得P1(1,-1).
此时
②若以AC为直角边,点A为直角顶点;
则过点A作AF∥BC,交抛物线
由题意,直线AF的解析式为
不难求得
同理,有
综上所述,在抛物线上存在点
使△ACP是以AC为直角边的等腰直角三角形.
方法二:①若以AC为直角边,点C为直角顶点;
则延长
过点
∵
∴△
∴
经检验点P1(1,-1)在抛物线
使得△
②若以AC为直角边,点A为直角顶点;则过点A作
且使得
得到等腰直角三角形△
同理可证△
∴
经检验点
使得△
用平移变化的想法解题:
解法三:①若点C为直角顶点,则C为
由
②若点A为直角顶点,可知
由点C向右平移1个单位长度、向上平移2个单位长度得到A,
可知P1(1,-1)经过同样的平移方式得到
