|
周末练习7(四边形部分的中考链接)
(一)选择题:
1.(08白银)如图:在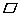 ABCD中,点E是CD的中点,AE的延长线与BC的延长线相交于点F,连结AC、 ABCD中,点E是CD的中点,AE的延长线与BC的延长线相交于点F,连结AC、
DF,则四边形ACFD是( )
A.梯形 B.菱形 C.正方形 D.平行四边形
2.(08湖南邵阳)如图,将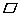 ABCD沿AE翻折,使点B恰好落在AD上的点F处,则下列结论不一定成立的 ABCD沿AE翻折,使点B恰好落在AD上的点F处,则下列结论不一定成立的
是( )
A.AF=EF B.AB=EF C.AE=AF D.AF=BE
3.(08四川巴中)如图,在 ABCD中,对角线AC和BD相交于点O,则下面条件能判定 ABCD中,对角线AC和BD相交于点O,则下面条件能判定 ABCD是矩形的 ABCD是矩形的
是( )
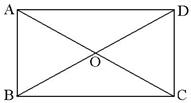
A.AC=BD B.AC⊥BD C.AC=BD且AC⊥BD D.AB=AD
4.(08山东威海)将矩形纸片ABCD按如图所示的方式折叠,得到菱形AECF。若AB=3,则BC的长为( )

A.1 B.2 C. D. D.
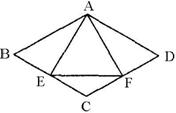
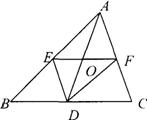
5.(08山东临沂)如图,菱形ABCD中,∠B=60°,AB=2,E、F分别是BC、CD的中点,连接AE、EF、
AF,则△AEF的周长为( )
A.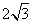 B. B.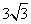 C. C.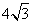 D.3 D.3
6.(08哈尔滨)如图,将边长为8cm的正方形纸片ABCD折叠,使点D落在BC边中点E处,点A落在点F处,
折痕为MN,则线段CN的长是( )
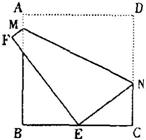
A.3cm B.4cm C.5cm D.6cm
7、(08四川渭田)如图,将一块边长为12的正方形纸片ABCD的顶点A折叠至DC边上的点E,使DE=5,折
痕为PQ,则PQ的长为( )
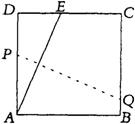
A.12 B.13 C.14 D.15
8.(08沈阳)如图所示,正方形ABCD中,点E是CD边上一点,连接AE,交对角线BD于点F,连接CF,则
图中全等三角形共有( )
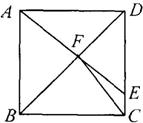
A.1对 B.2对 C.3对 D.4对
9.(08山东潍坊)如图,梯形ABCD中,AD∥BC,AD=AB,BC=BD,∠A=100°,则∠C=( )
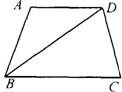
A.80° B.70° C.75° D.60°
10.(08四川眉山).如图,在梯形ABCD中,AD∥BC,AB=a,DC=b,DC边的垂直平分线EF交BC边于E,
且E为BC边的中点,又DE∥AB.则梯形ABCD的周长等于( )
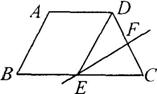
A.2a+26 B.3a+b C.4a+b D.5a+b
(二)填空题:
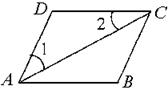
11.(08赤峰).如图,已知AC平分∠BAD,∠1=∠2,AB=DC=3,则BC=________。
12.(08福建).如图, ABCD中,CE⊥AB,垂足为E,如果∠A=115°,则∠BCE=________. ABCD中,CE⊥AB,垂足为E,如果∠A=115°,则∠BCE=________.
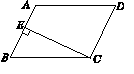
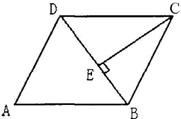
13.(08湖南怀化)如图,在平行四边形ABCD中,DB=DC、∠A=65°,CE⊥BD于E,则∠BCE=_______。
14.(08山东济南).如图,在△ABC中,EF为△ABC的中位线,D为BC边上一点(不与B、C重合),AD与
EF交于点O,连接DE、DF,要使四边形AEDF为平行四边形,需要添加条件____.(只添加一个条件)
15.如图,矩形纸片ABCD中,AD=9,AB=3,将其折叠,使点D与点B重合,折痕为EF,那么折痕EF的长
为________.
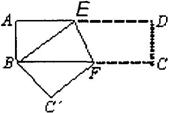
16.(08山东济南).如图:矩形纸片ABCD,AB=2,点E在BC上,且AE=EC.若将纸片沿AE折叠,点B恰
好落在AC上,则AC的长是________.

17.(08山东临沂).如图,矩形ABCD中,AB=2,BC=3,对角线AC的生直平分线分别交AD,BC于点E、
F,连接CE,则CE的长________.

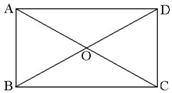
18.(08山东青岛).如图,在矩形ABCD中,对角线AC,BD相交于点O,若∠AOB=60°,AB=4cm,则
AC的长为________。
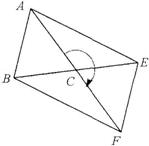
19.(08山东淄博).如图,在△ABC中,AB=AC,将△ABC绕点C旋转180°得到△FEC,连接AE,BF。
当∠ACB为________度时,四边形ABFE为矩形。
20.如图,菱形ABCD中,O是对角线AC,BD的交点,AB=5cm,AO=4cm,则BD=________cm.

21.(08浙江温州).如图,菱形ABCD中,∠A=60°,对角线BD=8,则菱形ABCD的周长等于________.
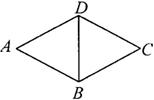
22.(08湖南长沙)、如图,P为菱形ABCD的对角线上一点,PE⊥AB于点E,PF⊥AD于点F,PF=3cm,则
P点到AB的距离是________cm.
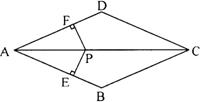
23.(08四川凉山).菱形ABCD中,AE垂直平BC,垂足为E,AB=4cm。那么,菱形ABCD的面积是_______,
对角线BD的长是________.
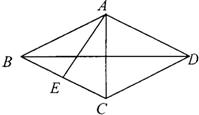
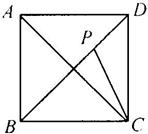
24.(08广东佛山).如图,已知P是正方形ABCD对角线BD上一点,且BP=BC,则∠ACP度数是______.
答案:
(一)选择题
1. D
2. C
3. A
4. D
5. B
6. A
7. B
8. C
9. B
10. C
(二)填空题
11.3
12.25°
13.25°
14.D是BC的中点
15.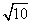
16.4
17.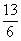
18.8
19.60°
20.6
21.32
22.3
23.
24.22.5°
|