|
二次根式
一、知识结构:
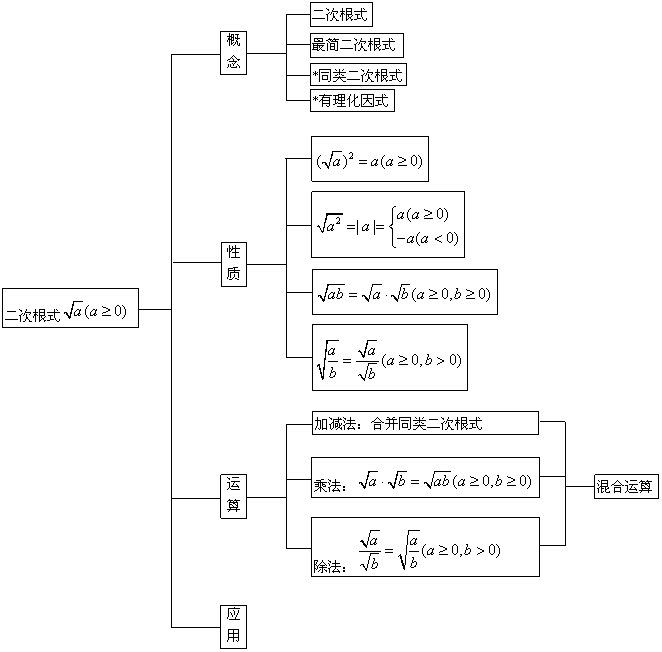
二、知识要点:
1.关于二次根式的概念,要注意以下几点:
(1)从形式上看,二次根式是以根号“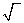 ”表示的代数式,这里的开方运算是最后一步运算。如 ”表示的代数式,这里的开方运算是最后一步运算。如
 , ,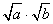 等不是二次根式,而是含有二次根式的代数式或二次根式的运算; 等不是二次根式,而是含有二次根式的代数式或二次根式的运算;
(2)当一个二次根式前面乘有一个有理数或有理式(整式或分式)时,虽然最后运算不是开方而是乘
法,但为了方便起见,我们把它看作一个整体仍叫做二次根式,而前面与其相乘的有理数或有理
式就叫做二次根式的系数;
(3)二次根式的被开方数,可以是某个确定的非负实数,也可以是某个代数式表示的数,但其中所含
字母的取值必须使得该代数式的值为非负实数;
(4)象“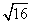 , ,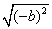 ”等虽然可以进行开方运算,但它们仍属于二次根式。 ”等虽然可以进行开方运算,但它们仍属于二次根式。
2.二次根式的主要性质:
(1)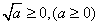 ; ;
(2)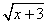 ; ;
(3)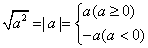 ; ;
(4)积的算术平方根的性质: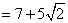 ; ;
(5)商的算术平方根的性质: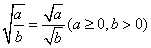 ; ;
(6)若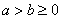 ,则 ,则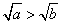 。 。
3.注意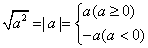 与 与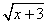 的逆用。 的逆用。
4.二次根式的运算:
(1)二次根式的乘除运算:二次根式相乘除,把被开方数相乘除,根指数不变。
由特殊到一般,理解二次根式乘除运算法则的合理性;
明确运算结果的要求,不断归纳运算结果应满足的两个要求:
①应为最简二次根式(包括两个条件)或有理式;②分母中不含根号。
(2)二次根式的加减运算:先将二次根式化为最简二次根式,再将被开方数相同的二次根式进行合
并。
二次根式的加减运算需要先化为最简二次根式,再类比整式加减运算中的合并同类项,二次根式
加减运算的实质是合并同类二次根式。
(3)二次根式的混合运算
整式的运算顺序、运算法则、公式和运算律在二次根式的运算中同样适用。
三、例题分析:
 1.下列各式中,哪些是二次根式?哪些不是二次根式?为什么? 1.下列各式中,哪些是二次根式?哪些不是二次根式?为什么?
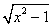 , ,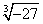 , ,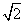 , ,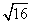 , ,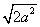 , , , ,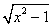 , ,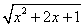 , ,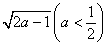 , ,
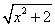 , ,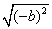 , ,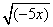 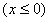 , ,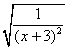 , ,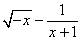 , ,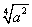 。 。
解:二次根式有: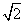 , ,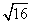 , ,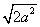 , ,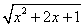 , ,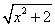 , ,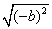 , ,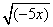 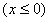
 2. 2.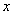 是怎样的实数时,下列各式在实数范围内有意义? 是怎样的实数时,下列各式在实数范围内有意义?
(1)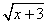 ;(2) ;(2)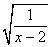 ; (3) ; (3)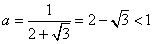 ; (4) ; (4)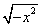 ; (5) ; (5) ; ;
(6)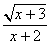 ;(7) ;(7)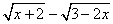 ; (8) ; (8)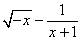 ;(9) ;(9) 。 。
解:(1)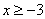 (2) (2)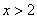 (3) (3)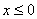
(4)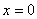 (5) (5)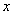 为任何数 (6) 为任何数 (6)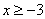 且 且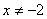
(7)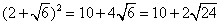 (8) (8)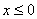 且 且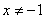 (9) (9)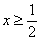 且 且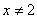
 3.当 3.当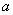 ________时, ________时,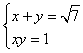 。 。
解:∵ 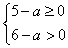 ∴ ∴ 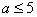
 4.在 4.在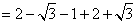 、 、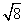 、 、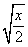 、 、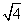 、 、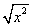 、 、 、 、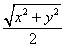 、 、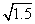 中,最简二次根式有____。 中,最简二次根式有____。
解析:最简二次根式满足:
(1)被开方数中不含有分母、分数、小数
(2)被开方数中因数或因式的指数小于根指数
∴ 最简二次根式有: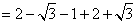 , , , ,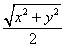 。 。
 5.在实数范围内分解因式: 5.在实数范围内分解因式: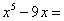 ________; ________;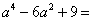 ________。 ________。
解析:原式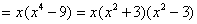 原式 原式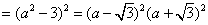
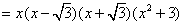
 6.若 6.若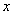 、 、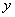 为实数, 为实数, 。求 。求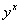 的值。 的值。
解:∵ 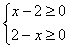 ∴ ∴ 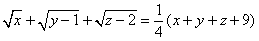 ∴ ∴ 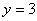 ∴ ∴ 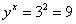
 7.已知 7.已知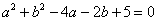 求 求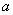 、 、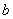 、 、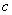 的值。 的值。
解:∵ 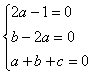 ∴ ∴ 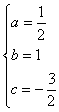
 8.已知 8.已知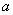 , ,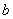 , ,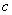 为三角形的三边,则 为三角形的三边,则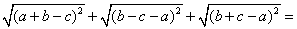 _____。 _____。
解:∵ 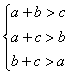 ∴ 原式 ∴ 原式 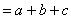
 9.比较大小(1) 9.比较大小(1) ;(2) ;(2)
解:(1)∵ 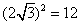 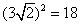 且 且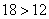
∴ 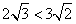
(2)∵ 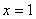 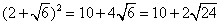
∴ 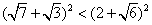 ∴ ∴ 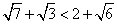
总结:常用的比较大小的方法
1.两上实数a,b比较大小,一般有“比”与“较”两种方法:
①将两个实数相除(比):若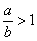 ,当 ,当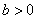 时,则 时,则 ;当 ;当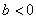 时,则 时,则 。 。
若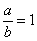 ,则 ,则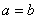
若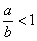 ,当 ,当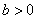 时,则 时,则 ;当 ;当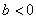 时,则 时,则 。 。
②将两个实数相减(较):若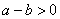 ,则 ,则 ; ;
若 ,则 ,则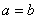 ; ;
若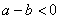 ,则 ,则 。 。
2.除此之外,还有以下常用方法:
(1)估算法; (2)被开方数比较法; (3)平方比较法;
(4)倒数的比较法; (5)设参数比较法; ※(6)分子有理化比较法。
练习:比较下列各根式或含有根式的代数式的大小:
(1) (2) (2)
(3) (4) (4)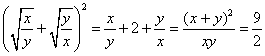
(5)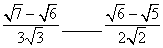 (6) (6)
答案:(1)> (2)>(3)> (4)< (5)< (6)<
 10.若最简二次根式 10.若最简二次根式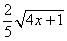 与最简二次根式 与最简二次根式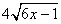 可以合并,则 可以合并,则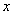 的取值为________。 的取值为________。
解:可以合并的根式是同类根式。
∴ 
∴ 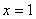
 11.①已知: 11.①已知: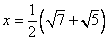 , ,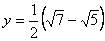 ,求 ,求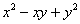 的值。 的值。
解:由已知: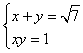 ∴ ∴ 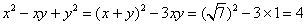
②已知: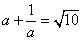 ,求:(1) ,求:(1)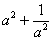 的值;(2) 的值;(2)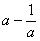 的值 的值
解:(1)∵ 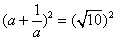 ∴ ∴ 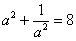
(2)∵ 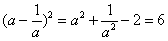 ∴ ∴ 
③已知: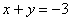 , ,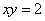 ,求 ,求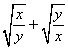 的值 的值
∵ 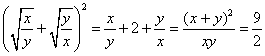
∴ 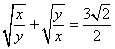
④已知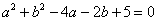 ,求 ,求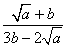 的值。 的值。
∵ 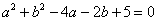
∴ 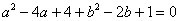
∴ 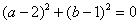
∴ 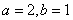
∴ 原式 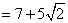
⑤已知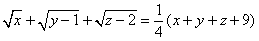 ,求 ,求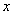 、 、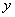 、 、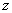 的值。 的值。
∵ 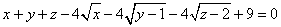
∴ 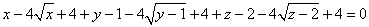
∴ 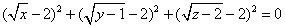
∴ 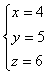
⑥已知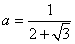 ,求 ,求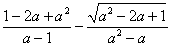 的值。 的值。
∵ 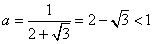
∴ 原式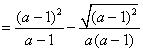
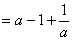
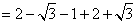
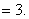
|