共150分    时间120分钟

    一、选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项符合题目要求，将正确答案的代号填入答题栏中）

    1.设A={1，2}，则满足A∪B={1，2，3}的集合B的个数是（    ）

        A．1                B.3                C.4                D.8

    2.若函数f(2x－1)的定义域为[0，2]，则f(x)的定义域为（    ）

    3.已知分段函数f(x)是奇函数，当x＞0时f(x)=(1－x)x，则x＜0，f(x)等于（    ）

        A．－x(1＋x)        B. x(1＋x)          C. －x(1－x)       D. x(1－x)

    4.下列结论正确的是（   ）

        A．偶函数的图象一定与y轴相交             B.若f(x)为奇函数，则一定有f(0)=0

        A．4                B.3                 C.2                D.1

    6.若y=log(x＋b)，（a＞0，且a≠1）的图象经过（－1，0），（0，1）则（    ）

    7.若f(x)是定义在R上的偶函数，在（－∞，0]上是减函数，且f(2)=0，使得f(x)＜0的x的取值范围是（   ）

        A．（－∞，2）       B.（2，＋∞）       C.（－∞，2）∪（2，＋∞） D.（－2，2）

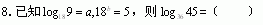
    9.三个数6^0.7，0.7⁶，log_0.76的大小顺序是（    ）

        A．log_0.76＜0.7⁶＜6^0.7                     B. 0.7⁶＜6^0.7＜log_0.76

        C．log_0.76＜6^0.7＜0.7⁶                     D. 0.7⁶＜log_0.76＜6^0.7

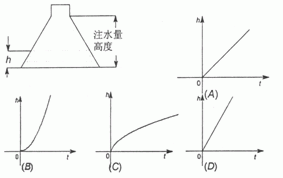
    10.用固定的速度向如下图形状的瓶子注水，则水面的高度h和时间t之间的关系是（    ）

    11. f(x)=2ax²－x－1在（0，1）内恰有一个零点，则实数a的取值范围（    ）

        A．a＞1             B. a≥0            C. a＜1               D. a≥1

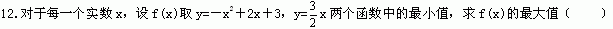
        A．0                B.4                C.3                   D.2

    二、填空题（本大题共4小题，每小题4分，共16分，把答案填入题中的横线上）

    13.A={y|y=x＋1}，B={y|y=x²－x－2}，则A∩B=             。

    14.已知f(x－1)=x²－2x，求f(x)的解析式为                。

    三、解答题（本大题共6小题，共74分，解答应写出文字说明、证明过程或演算步骤）

    17.（12分）已知A={x∈R|x²－3x＋2=0}，B={x∈R|ax－2=0}，且A∪B=A。求实数a的值组成的集合C。

    18.（12分）已知M={a，b}，N={－1，0，1}

    （1）写出从集合M到集合N的映射；

    （2）若从M到N的映射f满足：f(a)＋f(b)=0，问这样的映射有多少个？

    （1）求f(x)的定义域；

    （2）作出函数图象；

    （3）判断并证明f(x)在（－∞，－1]上的单调性（写出用定义证明的过程）

    22.（14分）在R上定义运算V：xVy=x(y＋1)，函数f(x)=(x＋m)V(x－3)＋5＋m。若f(x)的零点都大于2，求m的取值范围。