|
数学试卷
一、单项选择题(每题5分,满分60分。)
1.定义A-B={x|x∈A,且x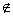 B},如果M={1,2,3,4,5},N={2,3,6},则M-N等于( ) B},如果M={1,2,3,4,5},N={2,3,6},则M-N等于( )
A. M B.N C.{1,4,5} D.{6}
2.命题“方程|x|=2”的解是x=2或x=-2中,使用的逻辑词的情况是( )
A.没有使用 B.或 C.且 D.非
3.设原命题“若p则q”真而逆命题假,则p是q的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
4.下列函数中,与y=x是同一函数的是( )
A.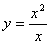 B. B.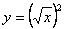 C. C. D. D.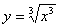
5.若(x,y)在映射f下的象是(x+y,x-y),则(1,2)在f下的原象是( )
A.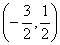 B. B.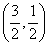 C. C. D. D.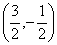
6.函数 的单调递增区间( ) 的单调递增区间( )
A.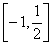 B. B.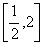 C. C. D. D.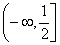
7.函数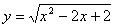 , ,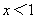 。则它的反函数的定义域是( ) 。则它的反函数的定义域是( )
A.(-∞,1) B.(1,+∞) C. D. D.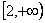
8.已知a=0.80.8,b=0.8 0.9,c=1.20.8,则a、b、c三者的大小数是( )
A.c>a>b B.a>b>c C.c>b>a D.b>a>c
9.如果 ( ) ( )
A.lg2lg3 B.lg2+lg3 C. D.-6 D.-6
10.在等差数列{an}中,已知前10项和5,前20项和15,求前30项的和( )
A.15 B.10 C.20 D.30
11.设A和G分别是x,y的等差中项和等比中项,则x2+y2等于( )
A.2A2-G2 B.4A2-2G2 C.4A2-G2 D.2A2-2G2
12.在等比数列中,a7=6,a9=9,则a5=( )
A.3 B.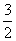 C.4 D.2 C.4 D.2
二、填空题(每 小 题4分 ,共 16分)
13. 函数y= 的定义域是 。 的定义域是 。
14.已知f(x)=x3+a,且f(-1)=0,则f (2)的值是 。
15.若¦(x)=(k-2)x2+(k-1)x+3是偶函数,则¦(x)的单调递增区间是_________。
16. 已知等差数列{an},以(n,an)为坐标的点均在直线y=2kx-(k-12)上,并从a5开始各项均小于零,则d的取值范围 .
三、解答题 ( 共74分 )
17.解不等式(12分)
(1) >0 >0
(2) x2-3x-10≤0
18.(12分)求值: +(log318-log32)2+ +(log318-log32)2+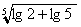
19.(12分)在等差数列{an}中,a4=9,a8=21,求d及S11。
20.(本 题 满 分 12分 )
已知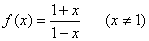
(1)求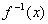 ; ;
(2)判断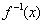 在(1,+ 在(1,+ )是增函数,还是减函数?并用增减函数的定义证明你的判断。 )是增函数,还是减函数?并用增减函数的定义证明你的判断。
21.(本题满分12分)已知f(x)=x2-2(n+1)x+n2+5n+3。
(Ⅰ)设f(x)的图像的顶点的纵坐标构成数列{an},问:数列{an}是等差还是等比数列,并求其公差d(或公比q)及通项an。
(Ⅱ) 若从数列{an}中依次取出第2、4、8…2n,…项,按原来的顺序排列成一个新的数列,试求新数列的前n项的和为An。
22.(本题满分14分)某租赁公司拥有汽车100辆,当每辆车的月租金为3000元时,可全部租出;当每辆车的月租金每增加50元时未租出的车将会增加一辆,租出去的车每辆每月需要维护费150元, 未租出去的车每辆每月需要维护费50元。
(Ⅰ)当每辆车的月租金定为3600时,能租出多少辆车?
(Ⅱ)当每辆车的月租金多少时,租赁公司的月收益最大?最大月收益为多少元?
2006年湖南长沙市天心一中高一上学期期末考试
数学试卷
参考答案
一、选择题
1.C 2.B 3.A 4.D 5.D 6.A
7.B 8.A 9.C 10.D 11.B 12.C
二、填空题:
13.{x∣–3≤ x ≤3};
14.9;
15.(- ,0); ,0);
16.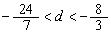
三、解答题:
17.(1)-5< x <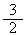
(2)-2≤x≤5
18.解:原式=4+4+1=9
19.解:d=3 S11=165
20.解:(1)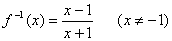 (4分) (4分)
(2)令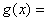  ,则 ,则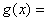  , , 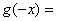 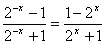 , ,
 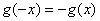 , , 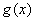 是奇函数,即 是奇函数,即 是奇函数。 (4分) 是奇函数。 (4分)
(3)增函数 (2分)
证明略
21.解:(Ⅰ)等差数列 , an =3n+2 , d=3
(Ⅱ)An=a2+a4+a8+…+a2n=(3×2+2)+(3×4+2)+(3×8+2)+ …+(3×2n+2)
=3×(2+4+8+…+2n)+2n
=3×2n+1+2n-6
22.题:解:(Ⅰ)当每辆车的月租金定为3600时,未能租出的车辆数为:
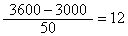
(Ⅱ)设每辆车的月租金为x元,则租赁公司的月收益为
f(x)= 
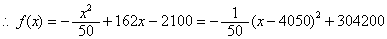
所以,当x=4050时, f(x)最大,最大值为f(4050)=307050
所以,当每辆车的月租金为4050元时,租赁公司的月收益最大,最大月收益为307050元。
|