|
集合的表示方法
(一)重点知识理解与简单应用
知能点1 集合的表示方法自主迁移
1.用列举法表示下列集合.
(1)不大于10的非负偶数集;
(2)自然数中不大于10的质数集;

(4){自然数中五个最小的完全平方数};
(5){x|(x-1)2(x-2)=0};
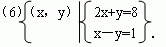
2.用描述法表示下列集合:
(1){3,6,9,12,15};
(2){1,2,4,8,16};
(3){1,7,11,12}.
3.用适当方法表示下列集合.
(1)由所有非负偶数组成的集合;
(2)由所有小于20的既是奇数又是质数的正整数组成的集合;
(3)方程(x-1)(x-2)(x2-5)=0的解组成的集合;
(4)以A为圆心,m为半径的圆上所有点组成的集合.
4.判断下列对象能否构成集合,如果能请用适当方法表示该集合,如不能请说明理由.
(1) 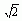 近似值的全体; 近似值的全体;
(2)正三角形的全体;
(3)方程x2-2x-3=0的实数解.
知能点2 集合的分类
5.判断下列各组集合中哪些是有限集,哪些是无限集,哪些是空集.
(1)全世界的人组成的集合;
(2)小于1的正数集合;
(3)大于0小于100的偶数集;
(4)高一年级所有的学生集合;
(5)方程(x-1)(x-2)(x-3)=0的解集;
(6)方程x2+7x+100=0的实数解集.
(二)学科内综合
综合 利用集合元素的特性和方程的联系解决问题
6.已知集合A={x|ax2+2x-3=0,a∈R},若A中只有一个元素,判断集合{x|ax+3=0}是有限集、还是无限集、还是空集?
(三)创新拓展实践
7.某学校组织运动会,运动员从1号开始编排共有261名运动员参赛,用适当方法表示运动员编号集合,并说明是有限集还是无限集.
新课标梯度评价
基础巩固
1.(知能点1)下列集合表示正确的是( )
A.{3,3,2} B.{全体实数} C.{正整数} D.方程x2-2x+1=0的解集为{x2-2x+1=0}
2.(知能点1)将集合{2,4,6,8}用描述法表示正确的有( )
①{x|x是大于0小于10的偶数}; ②{x|2≤x≤8}; ③{x|(x-2)(x-4)(x-6)(x-8)=0};
④{x|x是2的倍数}; ⑤{x|x=2n,1≤n≤4,n∈N}.
A.①②③ B.①③④ C.②③⑤ D.①③⑤
3.(知能点1)将集合 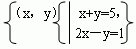 表示成列举法,正确的是( ) 表示成列举法,正确的是( )
A.{2,3} B.{(2,3)} C.{x=2,y=3} D.{2,3}
4.(知能点1)下列对象能否构成集合,若能,则用适当方法表示该集合;若不能,则说明理由.
(1)高一(1)班全体女学生; (2)高一(1)班全体胖学生;
(3)高一年级所开设的全部课程; (4)高一(2)学生的平均身高.
5.(知能点1)用适当方法表示下列集合.
(1)大于1小于10的奇数; (2)12的正约数;
(3)能被5整除的两位正整数; (4)方程3x+5=0的解集;
(5)平面直角坐标系内坐标轴上的点.
6.(知能点2)判断下列集合是有限集、无限集,还是空集?
(1){x|x5-1=0,x∈R}; (2){x|3x-5>0};
(3)方程x2+x-1=0的解; (4)2x2+x+1=0的解.
能力培养
7.(综合)设集合A={(x,y)|3x+y=5,x∈N,y∈N},试用列举法表示集合A.
8.(综合)集合M={x∈Z|1≤x≤4},N={y2-1| y∈M},试用列举法表示集合M,N.
创新拓展
9.(创新应用)已知集合A={a|a2+ka-k-1=0},A中的元素不在集合{4,7,10}中,A中只有一个元素在集合{2,3,4,7,10}中,求集合A.
|