|
1.2.2 集合的运算
第一课时
（一）重点知识理解与简单应用
知能点1 交集的概念
自主迁移
1．已知M=｛y|y=x2+1,x∈R｝,N=｛y|y=－x2+1,x∈R｝,则M∩N是（ ）
A．｛0，1｝ B．｛（0，1）｝ C．｛1｝ D．以上都不对
2．已知M=｛x|x是平行四边形｝,P=｛x|x是梯形｝,则M∩P等于（ ）
A．M B．P C．｛x|x是平行四边形且是梯形｝ D．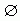
3．已知集合M=｛（x，y）|x+y=2｝,N=｛（x，y）|x－y=4｝,那么集合M∩N为（ ）
A．x=3，y=－1 B．（3，－1） C．｛3，－1｝ D．｛（3，－1）｝
知能点2 交集的性质及简单应用
4．若｛3，4，m2－3m－1｝∩｛2m，－3｝=｛－3｝，则m= ．
5．集合A=｛1，2，3，4｝，B A，且1∈（A∩B），4∈（A∩B），则满足上述条件的集合B的个数是（ ）
A．1 B．2 C．4 D．8
知能点3 并集的概念
6．满足｛1，3｝∪A=｛1，3，5｝的所有集合A的个数是（ ）
A．1 B．2 C．3 D．4
知能点4 并集性质及简单应用
7．设M=｛0，1，2，4，5，7｝，N=｛1，4，6，8，9｝，P=｛4，7，9｝，则（M∩N）∪（M∩P）等于（ ）
A．｛1，4｝ B．｛1，7｝ C．｛4，7｝ D．｛1，4，7｝
8．若集合A、B、C满足A∩B=A，B∪C=C，则A与C之间的关系必定是（ ）
（二）学科内综合
综合 综合运用交集和并集的性质
9．设集合A=｛x2，2x－1，－4｝，B=｛x－5，1－x，9｝，若A∩B=｛9｝，求A∪B．
（三）创新拓展实践
10．某学校组织运动会参加田赛的运动员占运动员总数的60%．参加径赛的运动员占运动员总数的70%，两项都参加的运动员有60名，问全校共有多少名运动员参加了比赛？
新课标梯度评价
基础巩固
1．（知能点1）集合A=｛x|x＜－3，或x＞3｝，B=｛x|x＜1，或x＞4｝，则A∩B= ．
2．（知能点2）集合A=｛a2，a+1，－3｝，B=｛a－3，2a－1，a2+1｝，若A∩B=（－3），则a的值为（ ）
A．0 B．1 C．2 D．－1
3．（知能点1、3）已知A∩B= ，M=｛A的子集｝，N=｛B的子集｝，则下列各式成立的是（ ）
A．M∩N=○ B．A∪B=M∩N C．M∩N=｛｝ D．A∪B=M∪N
4．（综合）设A=｛x∈Z|x2－px+15=0｝，B=｛x∈Z|x2－5x+q=0｝，若A∪B=｛2，3，5｝，则A、B分别为（ ）
A．｛3，5｝，｛2，3｝ B．｛2，3｝，｛3，5｝
C．｛2，5｝，｛3，5｝ D．｛3，5｝，｛2，5｝
5．（综合）下列4个推理①a∈（A∪B） a∈A；②a∈（A∩B） a∈（A∪B）；③A B A∪B=B；④A∪B=A A∩B=B，其中正确的个数是（ ）
A．1 B．2 C．3 D．4
6．（知能点3）若A∪B=○，则（ ）
A．A=，或B= B．B=○，或A≠ C．A=B=○ D．A≠，或B≠
7．（知能点2）已知集合A、B、C为非空集合，M= A∩C，N= B∩C，P=M∪N，则一定有（ ）
A．C∩P=C B．C∩P=P C．C∩P=A D．C∩P=
8．（知能点2）已知集合X=｛x|x=2m，m∈Z｝，Y=｛y|y=4n+2，n∈Z｝，则X与Y关系为（ ）
9．（综合）已知集合A∪B=｛a，b，c，d｝，A=｛a，b｝，则集合B的子集最多可能有的个数为（ ）
A．8 B．16 C．4 D．2
10．（知能点2）已知集合A=｛x|x2+ x+1=0｝，若A∩R=○，则实数m的取值范围为（ ）
A．m＜4 B．m＞4 C．0＜m＜4 D．0≤m＜4
11．（综合）已知集合A=｛a，b｝，B=｛x|x∈A｝，C=｛x|x A｝，试用列举法写出集合B、C，并说明B、C之间的关系．
12．（综合）设A=｛x|（x+2）（x－4）＞0｝，B=｛y|x≤y＜x+3｝，问x为何值时，
（1）A∩B=； （2）A∩B≠ （3）A∩B=B．
13．（综合）已知A=｛x|x2－px+15=0｝，B=｛x|x2－ax－b=0｝，且A∪B=｛2，3，5｝，A∩B=｛3｝，求p，a，b的值．
创新拓展
14．（知能点2）设A=｛（x，y）y=x2+2x+5｝，B=｛（x，y）y=mx+m－1｝．问：
（1）m为何值时A∩B有两个元素；
（2）m为何值时A∩B至多有一个元素．
15．（知能点2）已知集合A=｛x|x2－ax+a2－37=0｝，B=｛x|x2－7x+12=0｝，C=｛x|x2－2x－8=0｝求a为何值时，A∩B ○，与A∩C=同时成立．
16．（创新应用）某公司为了提高职工的业务素质，举办职工技能大赛，共考查三种专业技能，通过第一种技能考查的人数为45人，通过第二种技能考查的占总人数的80%．全部通过第三种技能考查，同时通过第一种和第二种技能考查的占总人数的70%，问该公司总共有多少职工？
第2课时
（一）重点知识理解与简单应用
知能点1 全集与补集的概念
1． 已知集合U=｛x≤10且x∈N｝，A=｛x|x是6的正约数｝，求CuA．
知能点2 补集的性质及应用
2．已知集合U=｛1，2，3，4，5，6｝，A=｛2，3，a｝，CuA=｛1，5，4｝，求a的值．
（二）学科内综合
综合 利用数形结合解相关问题
3．已知全集U，M、N是U的非空子集，若CuM N，则有（ ）
A．M CuN B．M CuN C．CuM= CuN D．M=N
4．已知全集S和集合M、N、P，M=CsN，N=CsP，则M与P的关系是（ ）
A．M= CsP B．M=P C．P M D．M P
5．设集合A=｛x|－3≤x≤a｝，B=｛y|y=3x+10，x∈A｝，C=｛z|z=5－x，x∈A｝，且B∩C=C，求实数a的取值范围．
6．（1999年全国）设集合M=｛x|－1≤x＜2＝，N=｛x|x－k≤0｝，若M∩N≠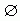 ，则k的取值范围是（ ）
A．（－ ，2］ B．［－1，+ ） C．（－1，+ ） D．［－1，2］
（三）创新拓展实践
7．某班50名学生，参加数学、外语学科竞赛，已知参加数学竞赛的人数是全班人数的 ,参加外语竞赛的人数比参加数学竞赛的人数多3人，两科都没参加的人数比同时参加数学、外语竞赛的人数的 多1人，求两科都参加的人数和两科都没参加的人数各是多少？
新课标梯度评价
基础巩固
1．（知能点1）设全集U=｛0，1，2，3，4｝，集合A=｛0，1，2，3｝，集合B=｛2，3，4｝，则由CuA与CuB的所有元素组成的集合为（ ）
A．｛0｝ B．｛0，1｝ C．｛0，1，4｝ D．｛0，1，2，3，4｝
2．已知全集U，集合M、N满足M∪N=U，那么下列关系中一定正确的是（ ）
A．N 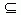 （CuM） B．M∩N=○ C．（CuM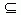） N D．（CuM）∪（CuN）=U
3．（知能点2）已知U=｛x|－1≤x≤3｝，M=｛x|－1＜x＜3｝，N=｛x|x2－2x－3=0｝，P=｛x|－1≤x＜3｝，则有（ ）
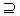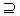A．CuM=N B．CuN=P C．CuM P D．M P
4．（综合）下列命题正确的是（ ）
A．Cu（CuP）=｛P｝ B．若M=｛1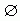，｛2｝｝，则｛2｝ M
C．CRQ=Q D．若N=｛1，2，3｝，S=｛x|x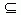N｝，则N∈S
5．（学科内综合）给出下列命题：
①CuA=｛x|x∈A｝； ②Cu=U；
③若S=｛三角形｝，A=｛钝角三角形｝，则CsA=｛锐角三角形｝；
④若U=｛1，2，3｝，A=｛2，3，4｝，则CuA=｛1｝．
其中正确命题的序号是 ．
6．（学科内综合）用集合的交、并、补表示1-2-10中集合的阴影部分为① ；② ；③ ．
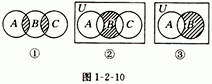
7．（知能点1）设全集U=｛小于10的自然数｝，集合A=｛小于10的正偶数｝，B=｛小于10的正质数｝，求CuA，CuB．
8．（知能点2）设全集U=｛2，0，3－a2｝，P=｛2，a2－a－2｝，CuP=（－1），求a的值．
9．（知能点1）设全集U=｛1，2，3，4，5｝，A=｛x|x2－5x+q=0，x∈U｝，求q的值及CuA．
10．（知能点2）设全集U=｛（x，y）|x∈R，y∈R｝，A=｛（x，y）|x2+y2≠0，x∈R，y∈R｝，用列举法表示CuA ．
能力培养
11．（学科内综合）用集合表示图1-2-11中的阴影部分是 ．
12．（学科内综合）已知全集U=｛（x，y）|x∈R，y∈R｝，集合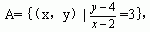 B=｛（x，y）|y=3x－2｝，则（CuA）∩B= ．
13．（综合）已知全集U=｛x|－4≤x≤4，x∈Z｝，A=｛－1, a2+1, a2－3｝，B=｛a－3 ，a－1，a+1｝，且A∩B=（－2），求Cu（A∪B）．
创新拓展
14．（学科与生活）在一次考试中，某班有36人的数学成绩不低于80分，有20人物理成绩不低于80分，且15人的物理、数学成绩都不低于80分，那么有多少人在两科成绩中至少一科不低于80分？若全班有50人，则两科都达不到80分的有几人？
15．（创新应用）对某村家庭拥有洗衣机、冰箱、彩电的情况进行统计，统计表如下，那么该村中拥有三种电器的家庭与全村家庭总数的比例应为（ ）
|
拥有电器种类 |
与全村家庭总数的比例 |
|
洗衣机 |
72% |
|
冰箱 |
64% |
|
彩电 |
80% |
|
洗衣机和冰箱 |
52% |
|
洗衣机和彩电 |
56% |
|
冰箱和彩电 |
52% |
|
都没有 |
2% |
A．42% B．44% C．48% D．52%
|
