|
一次函数的性质与图象
自主迁移
1、已知直线y=（a+2）x-4a2+4.
（1）a为何值时，这条直线经过原点； （2）a为何时时，这条直线与y轴交于点（0，-2）；
（3）a为何时时，这条直线这点（1，0）； （4）a为何时时，这条直线平行于直线y=-x。
2、已知y+5与3x+4成正比例，当x=1时，y=2。
（1）求y与x的函数关系式； （2）求当x=－1时的函数值； （3）如果y的取值范围0≤y≤5，求x的取值范围。
3、一根弹簧的原长是12cm，它能挂的重量不超过15kg，并且每挂重1kg就伸长![]() cm，挂职重后的弹簧长度y（cm）与挂重（kg）是一次函数的关系。
（1）求y与x的函数解析式； （2）求自变量x的取值范围； （3）画出这个函数的图象。
4、某船在静水中的速度为10km/h，现在船在如图2-2-2所示的Y字形的河中，由A逆流到相距12km的B地，然后又沿另一支流顺流而下到C地。A、B间的水速为4km/h，B、C间的水速为6km/h，写出船行距离y（km）与船行时间x（h）之间的关系式，并作出图像。
![]()
新课标梯度评价
基础巩固
1.（知能点1）下列函数中既是一次函数，又是正比例函数的是（ ）
A、y=-5x2 ![]() C、y=5x+1 D、y=5x
2.（知能点2）已知一次函数y=（1+2m）x-3，若y随x的增大而减小，则m的取值范围是（ ）
![]()
![]()
A、2 B、－1 C、2或－1 D、0或2
4.（知能点2）已知直线y=kx+b且过点A（x1，y1）和B（x2，y2），若k＜0，且x1＜x2，则y1与y2的大小关系是（ ）
A、y1＞y2 B、y1＜y2 C、y1=y2 D、不能确定
5.（知能点2）下列函数中，y随x的增大而增大的是（ ）
![]()
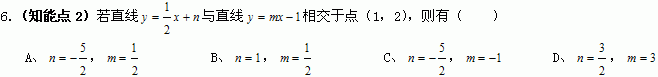
7.（知能点2）如果函数y=ax+2与y=bx+3的图象相交于x轴上一点，那么a，b的关系是（ ）
A、a=b B、a：b=2：3 C、a+2=b+3 D、a·b=1
8.（知能点1）函数y=kx+b的图象经过P（3，-2）和Q（-1，2），则这个函数解析式为（ ）
A、y=x-1 B、y=x+1 C、y=-x-1 D、y=-x+1
能力培养
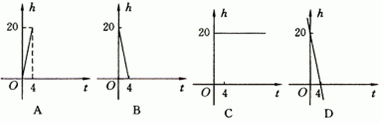
9.（知能点2）一根蜡烛长20cm，点燃后每小时燃烧5cm，燃烧时剩下的高度h（cm）与燃烧时间t（h）的函数关系用图象表示为下图中的（ ）
10.（知能点2）已知直线y=kx+4与两坐标轴围成的三角形面积为6，则k值为（ ）
11.（知能点1）已知某种产品5kg的价格为30元，那么这种产品7kg的价格是（ ）
A、210元 B、30元 C、42元 D、35元
12.（知能点1）一辆匀速行驶的火车90min行驶了180km，则这辆火车行驶的路程y（km）与时间t（h）之间的函数关系式是（ ）
A、y=2t B、y=120t C、y=2t （t≥0） D、y=120t（t≥0）
13.（知能点1）一等腰三角形的周长是20，则底边y是关于腰长x的函数，其解析式为（ ）
A、y=20-2x（x≤10） B、y=20-2x（x＜10） C、y=20-2x（5≤x≤10） D、y=20-2x（5＜x＜10）
14.（知能点2）某音像社对外出租光盘的收费方法是：每张光盘在租出后的头两天每天收0.8元，以后每天收0.5元，那么一张光盘在租出的第n天（n是正整数）应收租金 元。
创新拓展
15.（创新应用）《在华人民共和国个人所得税法》规定，公民全月工资、薪金所得不超过800的部分不必纳税，超过800元的部分为全月应纳税所得额，此项税款按下表分段累进计算：
|
全月纳税所得额 |
税率 |
|
不超500元的部 |
5% |
|
超过500～2000元的部分 |
10% |
|
超过2000～5000元的部分 |
15% |
|
… |
… |
某人一月份应交纳此税款26.78元，则它的当月工资所得介于（ ）
A、800～900元 B、900～1200元 C、1200～1500元 D、1500～2800元
16.为了保护学生的视力，课桌椅的高度都是按一定的关系配套设计的，研究表明：假设课桌的高度为y cm，椅子的高度为x cm，则y应是x 的一次函数。下表列出两套符合条件的课桌椅的高度：
|
|
第一套 |
第二套 |
|
椅子高度x（cm） |
40.0 |
37.0 |
|
桌子高度y（cm） |
75.0 |
70.2 |
（1）请你确定y与x的函数关系式（不必写出x的取值范围）；
（2）现有一把高42.0cm椅子和一张高78.2cm的课桌，它们是否配套？为什么？
|
