|
待定系数法
自主迁移
1、已知一个函数y=f(x),f(0)=3,又知当x=-3或x=-5时,这个二次函数的函数值为零,求这个二次函数的解析式。
2、函数y=ax2(a≠0)与直线y=2x-3交于点A(1,b)。
(1)求a和b的值;
(2)求抛物线y=ax2的解析式、顶点坐标、对称轴,并指出其开口方向;
(3)如果抛物线上另一点B与点A关于y轴对称,求点B的坐标;
(4) 求△OAB的面积。

A、第一象限
B、第二象限
C、第三象限
D、第四象限
4、已知集合A={x|x2-ax+a2-19=0},B={x|x2-5x+6=0},C={x|x2+2x-8=0},是否存在实数a,使得A∩C=Ø和A∩B≠Ø同时成立?若存在,求出a的值;若不存在,说明理由。
新课标梯度评价
基础巩固
1.(知能点)已知一次函数的图象经过(5,-2)和(3,4),求这个函数的解析式 。
2.(知能点)二次函数y=ax2+bx+c(a≠0)的图象顶点为(2,3),且过点(3,-1),则函数的解析式为 。
3.(综合)已知二次函数y=ax2+bx+c的图象经过点A(1,1),B(-1,4),C(3,0),求此函数的解析式。
4.(知能点)把y=3x2的图象向右平移2个单位长度,再向上平移5个单位长度,就可以得到函数 的图象。
5.(知能点)抛物线和y=2x2的图象形状相同,对称轴平行于y轴,且顶点在(-1,3),则它的解析式为 。
6.(知能点)二次函数y=-x2+bx+c的图象的最高点是(-1,3),则b、c的值为 。

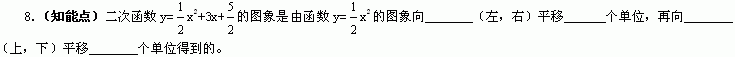
能力培养
9.(综合)已知抛物线的对称轴是x=-1,它与x轴交点间的距离等于4,它在y轴上的截距是-6,则它的解析式是 。
10.(综合)已知抛物线的顶点为(-1,-3),与y轴的交点为(0,-5),求此抛物线的解析式。
11.(综合)已知抛物线与x轴交于A(-1,0),B(1,0),并经过点M(0,1),求此抛物线的解析式。

13.(综合)若函数y=x2+(a+2)x+3,x∈[a,b]的图象关于直线x=1对称,则b= 。
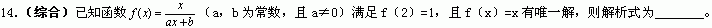
创新拓展
15.(创新应用)已知二次函数y=ax2+bx+c,当x=1时,y有最大值4,且|a|=1。
(1)求它的解析式;
(2)若上述图象与x轴交点为A、B,直线y=kx+m(k<0)过A、B中的一点与函数图象顶点G,且与y 轴交于点C,求直线解析式;
(3)求原点到所求直线的距离。
16.(创新应用)已知函数f(x)=x2-4ax+2a+30。
(1)求对一切实数x,f(x)的值均为非负实数的充要条件;

17.(创新应用)图2-2-12中折线是某电信局规定打长途电话所需付的电话费y(元)与通话时间t(分钟)之间的函数关系图象,根据图象填空:通话2分钟,需付电话费 元;通话5分钟,需付电话费 元;如果t≥3分钟,电话费y(元)与通话时间t(分钟)之间的函数关系式是 。

|