|
函数的单调性
自主迁移
1、下列函数中,在区间(0,2)上为增函数的是( )
A、y=3-x B、y=x2+1 C、![]() D、y=-|x| D、y=-|x|
2、有下列四个命题
①函数y=2x2+x+1在(0,+∞)上不是增函数; ②函数![]() 在(-∞,-1)∪(-1,+∞)上是减函数; 在(-∞,-1)∪(-1,+∞)上是减函数;
③函数![]() 的单调区间为[-2,+∞); ④已知f(x)在R上为增函数,若a+b>0,则有f(a)+f(b)>f(-a)+f(-b)。 的单调区间为[-2,+∞); ④已知f(x)在R上为增函数,若a+b>0,则有f(a)+f(b)>f(-a)+f(-b)。
其中正确命题的序号是 。

4、下列函数中,在区间(-∞,0]上为增函数的是( )
![]()
5、函数f(x)的定义域M内为增函数,且f(x)>0,则下列函数在M内不是增函数的是( )
![]()
6、已知y=f(u),u=g(x)的定义域为R,且y是u的减函数,u是x的增函数,判断y=f[g(x)]的增减性并证明。

8.已知A=[1,b](b>1),对于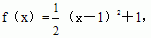 若x∈A时,f(x)∈A,试求b的值域。 若x∈A时,f(x)∈A,试求b的值域。
9、函数f(x)对任意的a、b∈R,都有f(a+b)= f(a)+ f(b)-1,并且当x>0时,f(x)>1。
(1)求证:f(x)是R上的增函数;
(2)若f(4)=5,解不等式f(3m2- m -2)<3
10、已知函数f(x)=x3-x在(0,a]上递减,在[a,+∞)上递增,求a的值。
11、(开放题)老师给出一个函数,三个学生正确地各指出了这个函数的一个性质:甲:在(-∞,1]上是减函数;乙:在[1,+∞)上是递增函数;丙:f(0)不是这个函数的最小值。 请你写出一个这样的函数。
新课标梯度评价
基础巩固
1.(知能点1)函数y=x2-6x-10在区间(2,4)上是( )
A、递减函数 B、递增函数 C、先递增再递减 D、先递减再递增
2.(知能点1)若一次函数y=kx+b在(-∞,+∞)上是减函数,则点(k,b)在直角坐标平面的( )
A、上半平面 B、下半平面 C、左半平面 D、右半平面
3.(知能点1)若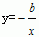 在(0,+∞)上减函数,则b的取值范围是 。 在(0,+∞)上减函数,则b的取值范围是 。
4.(知能点1)若函数f(x)=x2+2(a-1)x+2在区间(-∞,4)上是减函数,则实数a的取值范围是( )
A、a≤-3 B、a≥-3 C、a≤5 D、a≥3
5.(知能点1)已知函数f(x)是区间(0,+∞)上的减函数,那么f(a2-a+1)与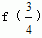 的大小关系是 。 的大小关系是 。
6.(知能点1,2)定义在R上的函数y=f(x)关于y轴对称,且在[0,+)上是增函数,则下列关系成立的是( )
A、f(3)<f(-4)<f(-π) B、f(-π)<f(-4)<f(3)
C、f(-4)<f(-π)<f(3) D、f(3)<f(-π)<f(-4)

8.(知能点1,2,3)如果二次函数f(x)=x2-(a-1)x+5在区间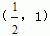 上是增函数,那么f(2)的取值范围是 。 上是增函数,那么f(2)的取值范围是 。
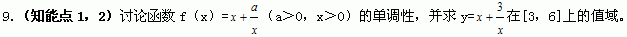
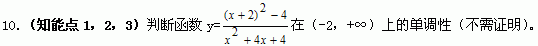
能力培养
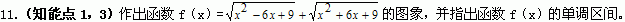
12.(知能点1,2)是否存在实数λ,使函数f(x)=x4+(2+λ)x2+2-λ在区间(-∞,-2]上是减函数,在区间[-1,0)上是增函数?若存在,求出λ的取值范围;若不存在,请说明理由。
13.(综合1)已知2x3-3x≤0,则函数f(x)=x2+x+1的最值情况为( )
A、有最小值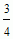 ,但无最大值 B、有最小值 ,但无最大值 B、有最小值![]() ,有最大值1 C、有最小值1,有最大值 ,有最大值1 C、有最小值1,有最大值![]() D、无最小值,也无最大值 D、无最小值,也无最大值
14.(综合2)如果函数f(x)=x2+bx+c对任意实数都有f(2+t)=f(2-t),那么( )
A、f(2)<f(1)<f(4) B、f(1)<f(2)<f(4) C、f(2)<f(4)<f(1) D、f(4)<f(2)<f(1)
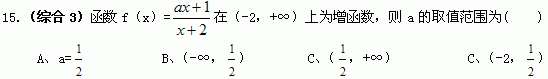
16.(综合2)函数f(x)定义在(0,+∞)上,且对x,y∈(0,+∞)均有f(xy)=f(x)+f(y),且在(0,+∞)上是增函数,若f(2)=1,解不等式f(x)+f(x-2)<3。
创新拓展
17.(创新应用)函数f(x)在区间[a,b]上具有单调性,且f(a)f(b)<0,则方程f(x)=0在区间[a,b]上( )
A、至少有一个实根 B、至多有一个实根 C、没有实根 D、必有唯一实根
18、(创新应用)已知函数y= f(x)的定义域是[a,b],当x∈[a,c]时,f(x)是单调增函数;当x∈[c,b]时,f(x)是单调减函数。试证明f(x)在x=c时取得最大值。
|