|
函数的零点
自主迁移
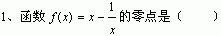
A、1 B、-1
C、1和-1 D、不存在
2、函数f(x)=x3-64x零点的个数是( )
A、0 B、3 C、1 D、2

4、对于函数f(x)=x2+mx+n,若f(a)>0, f(b)>0,则函数f(x)在区间(a,b)内( )
A、一定有零点
B、一定没有零点
C、可能有两个零点
D、至多有一个零点
5、若函数f(x)=x2+ax+b的两个零点分别是2和-4,求a,b的值。
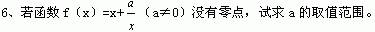
7、函数y=-2x2+x+3的自变量x在什么范围内取值时,函数值大于0,小于0,等于0?
8、若一元二次方程ax2+2x+1=0(a≠0)有一个正根和一个负根,则有( )
A、a<0 B、a>0
C、a<-1 D、a>1
9、已知二次函数f(x)=ax2+bx(a,b为常数,且a≠0)满足条件:f(-x+5)=f(x-3),且f(x)=x只有一个零点。
(1)求f(x)的解析式;
(2)是否存在实数m,n使f(x)的定义域和值域分别为[m,n]和[3m,3n],如果存在,求出m,n的值;如果不存在,说明理由。
新课标梯度评价
基础巩固
1.(知能点1)函数f(x)=x2+x+3的零点的个数是( )
A、0 B、1 C、2 D、3
2.(知能点1)若函数f(x)=x2+2x+a没有零点,则实数a的取值范围是( )
A、a<1 B、a>1 C、a≤1 D、a≥1
3.(知能点1)若函数f(x)=ax+b有一个零点2,那么函数g(x)=bx2-ax的零点是( )

4.(知能点2)若函数y=f(x)是偶函数,定义域为{x∈R|x≠0}且f(x)在(0,+∞)上是减函数,f(2)=0,则函数f(x)的零点有( )
A、唯一一个 B、两个
C、至少两个 D、无法判断

7.(知能点2,3)若函数f(x)=x2-ax-b的两个零点是2和3,则函数g(x)=bx2-ax-1的零点是 。
8.(知能点2,3)若函数f(x)=2(m+1)x2+4mx+2m-1的图象与x轴有两个交点,则实数m的取值范围是 。
能力培养
9.(知能点2)已知函数f(x)在区间(a,b)上单调且f(a)·f(b)<0,则函数f(x)在区间(a,b)上( )
A、至少有一个零点 B、至多有一个零点
C、没有零点 D、必有唯一零点
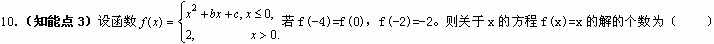
A、1 B、2 C、3 D、4
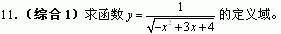
12.(知能点2)已知函数f(x)的图象是连续不断的,有如下x、f(x)的对应值表:
|
x |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
f(x) |
14 |
8 |
-2 |
2 |
7 |
3 |
-2 |
-1 |
8 |
问函数f(x)在哪几个区间内有零点?为什么?
13.(知能点3,综合1)二次函数y=ax2+bx+c(x∈R)的部分对应值如下表:
|
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
|
y |
6 |
0 |
-4 |
-6 |
-6 |
-4 |
0 |
6 |
则使ax2+bx+c>0的自变量x的取值范围是。
14.(综合2)已知函数f(x)=ax3+bx2+cx+d的图象如图2-4-3所示,则b的取值范围是( )
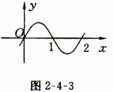
A、(-∞,0) B、(0,1)
C、(1,2) D、(2,+∞)
创新拓展
15.(综合2)已知f(x)=(x-a)(x-b)-2,并且α,β是函数f(x)的两个零点,则实数a,b,α,β间的大小关系可能是( )
A、a<α<b<β B、a<α<β<b
C、α<a<b<β D、α<a<β<b
16.(综合1,2)设二次函数f(x)=x2+x+a(a>0)满足f(m)<0,试比较f(m+1)与0的大小。
|