|
指数函数
第1课时
自主迁移
A.0个 B.1个 C. 2个 D. 3个
2.函数y=（a2-3a+3）ax是指数函数，则有（ ）
A.a=1或a=2 B.a=1 C.a=2 D.a>0,且a≠1
A.R,R B.R, (0，+∞)
C. (-∞,0)∪(0，+∞) , (-∞,1)∪(1，+∞) D. (-∞,0)∪(0，+∞) , (0,1)∪(1，+∞)
4.函数y=ax在[0，1]上的最大值与最小值的和为3，则a=（ ）
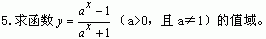
6.函数y=2x-3+3恒过定点 。
7.指数函数y=f（x）的图象经过点（2，4），那么f（2）·f（4）= 。
9.完成下列真空：
（1）1618与1816的大小关系是 。
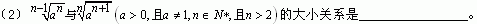
10.函数f(x)=x2-bx+c满足f(1+x)=f(1-x),且f(0)=3,则f(bx)与f(xx) 的大小关系是( )
A. f(bx)≤f(xx) B. f(bx) ≥f(cx)
C. f(bx)>f(cx) D. 大小关系随x的不同区间而改变
12.（课本变式题）家用电器（如冰箱等）使用的氟化物的释放破坏了大气上层的臭氧层，臭氧含量Q呈指数函数型变化，满足关系式Q=Q0e-0.0025t，其中Q0是臭氧的初始量。
（1）随时间的增加，臭氧的含量是增加还是减少？
（2）多少年后将会有一半的臭氧消失？
新课标梯度评价
基础巩固
1.（知能点1）指出下列函数哪些是指数函数？（ ）
2.（知能点2）函数f(x)=3-x-1的定义域、值域分别是（ ）
A.R,R B.R,(0,+∞) C. R,(-1,+∞) D.以上都不对
3.（知能点2）函数y=2-|x|的值域是（ ）
A.(0,1) B. (0,1] C. (0,+∞) D. (-∞,+∞)
4.（知能点1）已知函数y=ax-1+4(a>0，且a≠1)的图象恒过定点P，则点P的坐标是（ ）
A．（1，5） B.(1,4) C.(0,4) D.(4,0)
5.（综合）用“<”或“>”填空。
能力培养
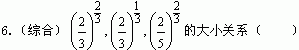
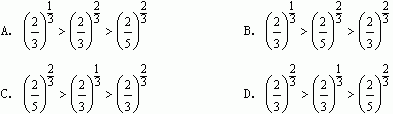
7.(知能点2)函数f(x)=(a2-1)x是R上的减函数，则|a|的取值范围是（ ）
A. a>0 B.a>1 C.0
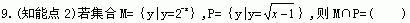
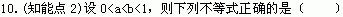
A.aab B.bab C. aaa D. bb < ab
11.(知能点2)设f(x)=3x+7,则f-1(x)的定义域为（ ）
A.（0，+∞） B. （7，+∞） C. （8，+∞） D.（-∞，+∞）
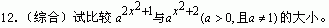
13．（知能2）函数在y=a2x+2ax-1(a>0，且a≠1)[-1,1]上有最大值14，求a的值。
创新拓展
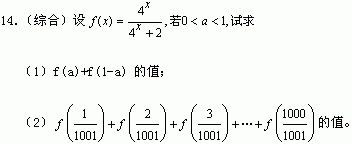
15.(创新应用)截止到1999年底我国人口约为13亿，如果今后能将人口平均增长优选法控制在1%，那么经过20年后，我国人口约为多少？（精确到亿）
第2课时
自主迁移
1.图3-1-4是指数函数（1）y=ax；（2）y=bx；（3）y=cx；（4）y=dx的图象，则a、b、c、d与1的大小关系为（ ）
2.函数y= 2x+1的图象是下图中的（ ）
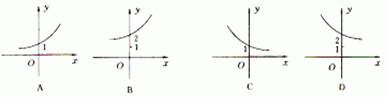
3.已知函数f(x)= 2x+a的图像不经过第二象限，则a的取值范围是 .
4.函数y= 3x的图象与函数y= -3-x的图象关于 轴对称。
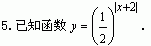
(1)画出该函数的图象；
(2)由图象指出函数的单调区间，并证明。
6.方程2x=2-x的解的个数为。
7.（高考真题）直线y=2a与函数y=|ax-1|(a >0,且a≠1)的图象有两个公共点，则a的取值范围是 。
8.当a>2时，函数y=ax和y=(a-1)x2的图象只能是下图中的（ ）
9.当a≠0时，函数y=ax+b和y=bax的图象只可能是下图中的（ ）
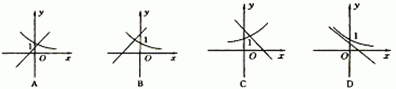
10.（数形结合题）已知函数f(x)=| 2x-1|的图象与直线y=a有一公共点，则a的取值范围是 。
11.（教材变式题）画出函数y= 2|x-1|的图象，并根据图象指出这个函数的一些重要性质。
新课标梯度评价
基础巩固
1.（知能点1）函数y= 2 -x的图象是下图中的（ ）
2.（知能点2）指数函数y= f(x)的图象经过点（2，4），那么f(3)·f(4)= 。
3. (知能点2)函数y= ax-1+1(a>0,且a≠1)中，无论a取什么值恒经过一个定点，则这个定点的坐标是 。
4.(知能点1)设a >1，-1x+b的图象必定不通过的象限是第 象限。
能力培养
5.（知能点1）函数y=2 x与y=x2的图象的交点个数是（ ）
A．0 B.1 C.2 D.4
6.（知能点2）函数y=ax-（b+1）(a >0,且a≠1) 的图象在第一、三、四象限，则必有（ ）
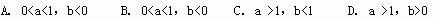
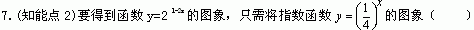
A.向左平移1个单位 B. 向右平移1个单位
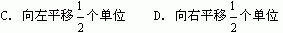
8.（知能点1）如果mx>nx对一切x>0都成立，则m、n的大小关系为（ ）
创新拓展
第3课时
自主迁移
1.求下函数定义域和值域。
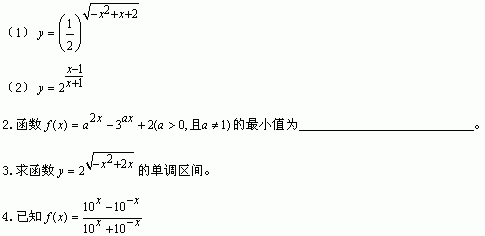
(1)判断函数奇偶性；
(2)证明f(x)是定义域内的增函数；
(3)求f(x)的值域。
（1）求的f(x)定义域和值域；
（2）判断f(x)与f(-x)的关系；
（3）讨论f(x)的单调性。
7.已知函数f(x)满足对任意x1,x2，当x12时，f(x1)2)且f(x1+x2)= f(x1)·f(x2)，则满足上述条件的一个函数是 。
10.设n为正整数，讨论函数f(n)=(n+1)·(0.9)n的增减性，并求当f(n)最大时的n的值。
新课标梯度评价
基础巩固
能力培养
（1）证明:不论a为何实数，f(x)均为增函数；
（2）试确定a的值，使f(x)为奇函数成立。
（1）求函数的定义域；
（2）判断函数的奇偶性；
（3）求证f(x)>0。
创新拓展
|
