|
函数的表示方法
第1课时
自主迁移
1、试用列表法表示0°,30°,45°,60°,90°角的正弦值和余弦值。
2、已知函数f(2x+1)=3x+2,且f(a)=4,则a= 。
3、(1)已知f(x+1)=x2-3x+2,求f(x)。
(2)已知 f(x)=-2x+1,求f[f(x)]。
知能点2 函数值域的求法
4、求下列函数的值域。

(二)学科内综合
综合 函数解析式的求法
5、已知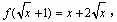 ,求f(x)与f(x-1)。 ,求f(x)与f(x-1)。
6、(2004年湖北)已知 ,则f(x)的解析式为 。 ,则f(x)的解析式为 。
7、(1)若a≠±1,x≠0时,函数f(x)满足方程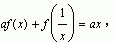 ,求f(x)的解析式; ,求f(x)的解析式;
(2)已知n为奇数,a≠1,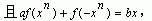 求f(x)的解析式。 求f(x)的解析式。
8、已知f(x)是一次函数,且满足3f(x+1)-2f(x-1)=2x+17,求f(x)。
9、已知f(x)为二次函数,且f(x+1)+f(x-1)=2x2-4x,求f(x)的表达式。
(三)创新拓展实践
10、是否存在正的自然数,a,b,使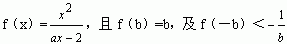 成立,若存在求出a,b的值,不存在说明理由。 成立,若存在求出a,b的值,不存在说明理由。
新课标梯度评价
1.(知能点1)若函数f(x)满足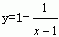 则f(2)的值为( ) 则f(2)的值为( )
A、1 B、-1 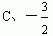 
2.(知能点1) 。 。
3.(知能点1)海面上的距离常用海里表示,1海里约合1852米。根据这一关系,米数y与海里数x的系数关系式为 。
4.(知能点1)设g(x)=1-2x, 。 。
5.(知能点1)已知函数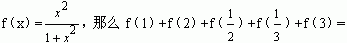 。 。
6.(知能点1)已知f(x)是正比例函数,g(x)是反比例函数,且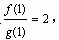 f(2)+4g(2)=6。求f(x)与g(x)的解析式。 f(2)+4g(2)=6。求f(x)与g(x)的解析式。
7.(知能点2)函数y=--x2-4x+1,x∈[-3,3]时的值域是( )
A、(-∞,5] B、[5,+∞) C、[-20,5] D、[4,5]
8.(知能点2)函数 的值域是( ) 的值域是( )

9.(知能点2)函数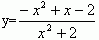 的值域为( ) 的值域为( )

10.(知能点2)函数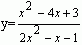 的值域是 。 的值域是 。
11.(知能点2)函数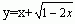 的值域是 。 的值域是 。
能力培养
12.(知能点2)已知函数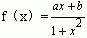 的最大值为4,最小值为-1,求实数a,b的值。 的最大值为4,最小值为-1,求实数a,b的值。
13.(综合)设f(x)=2x+3,g(x+2)=f(x),则g(x)=( )
A、2x+1 B、2x-1 C、2x-3 D、2x+7
14.(综合)设f(x)是一次函数,且2f(1)+3f(2)=3,2f(-1)- f(0)=-1,则f(x)= 。
15.(综合)求下列函数解析式:
(1)已知二次函数满足f(3x+1)=9x2-6x+5,求f(x)。
(2)已知f(x)为二次函数,且f(2x+1)+f(2x-1)=16x2-4x+6,求f(x)。
创新拓展
16.(探究题)是否存在实数a,c的值,使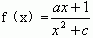 的值域为[-1,5],若存在,求出a,c的值;不存在,说明理由。 的值域为[-1,5],若存在,求出a,c的值;不存在,说明理由。
第2课时
(一)重点知识理解与简单的应用
知能点1 函数图象的画法
自主迁移
1、图2-1-7可表示函数图象的是( )
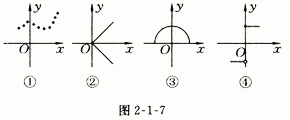
A、只有① B、②③④ C、①③④ D、②
2、设M={x|0≤x≤2},N={y|0≤y≤2},给出下列四个图形(如图2-1-8),其中能表示从集合M到集合N的函数关系的有( )
A、0个 B、1个 C、2个 D、3个

3、画出下列函数的图象。
(1)y=2x-3,x∈Z,且|x|≤2;
(2)y=|x-5|+|x+3|;
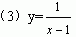
知能点2 分段函数
|
(1)在函数定义内,对于自变量x的不同取值范围,有着不同的对应法则,这样的函数通常叫分段函数。
(2)分段函数的定义域是各段定义域的并集,其值域是各段值域的并集。 |
4、作出函数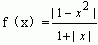 的图象。 的图象。
5、已知函数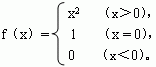
求f(1),f[f(-3)],f{f[f(-3)]}的值。
(二)学科内综合
综合1 对称、平移法作函数图像
6、函数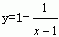 的图象是( ) 的图象是( )

7、已知函数y=f(|x|)的图象如图2-1-12所示,则函数y=f(x)的图不可能是( )

8、已知函数y=f(x)的图象如图2-1-13所示。请根据地上述图象作出下列函数的图象。
① y=f(-x);② y=-f(x);③ y=|f(x)|;
④ y=f(|x|);⑤ y=f(x-1);⑥ y=f(1-x)
综合2 数形结合
11、已知函数f(x)=2-x2,g(x)=r,定义F(x)=min{ f(x),g(x)},求F(x)的最大值(注:min表示最小值)。
新课标梯度评价
基础巩固
1、(知能点1)函数y=x+ 的图象为下图中的( )
2、(知能点1)函数y=ax2+bx+b与y=ax+b(ab≠0)的图象可能是图中的( )
3、(知能点1)在同一坐标系下,函数y=ax+ 与y=ax2的图象只能是( )
4、(知能点1)若[x]为不超过x的最大整数,则函数y=[x]的图象与y=x的交点个数为( )
A、0 B、1 C、2 D、无数
5、(知能点1)定义在(-∞,0)∪(0,+∞)上的函数f(x),它的图象关于y轴对称,它在(0,+∞)上的图象如图2-1-16所示,则不等式f(x)<0的解集为 。
6、(知能点1)作出函数y= 的图象,并说明该函数图象与y= 的图象之间的关系。
7、(知能点2)下列关于分段函数的叙述正确的有( )
①分段函数的定义域是在各段定义域的并集,值域是各段值域的并集;
②分段函数尽管在定义域不同的部分,有不同的对应法则,但它们是同一个函数。
③若D1,D2分别是分段函数的两个不同对应法则的值域,那么D1∩D2=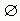 。 。
A、1个 B、2个 C、3个 D、0个
8、(知能点2)下列给出的函数是分段函数的是( )
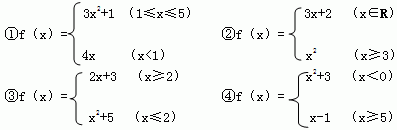
A、①②③ B、①④ C、②④ D、④
9、(知能点2)在函数 中,f(x)=3,则x= 。 中,f(x)=3,则x= 。
10、(知能点1、2)函数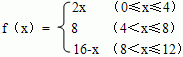 的最大值为 ,最小值为 。 的最大值为 ,最小值为 。
11、(知能点1、2)作出函数y=2 | x-1 | - 3 | x | 的图象,并求出其最大值。
能力培养
12、(知能点1、2)“依法纳税是每个公民应尽的义务”,国家征收个人所得税是分段计算的,总收入不超过800元,免征个人所得税,超过800元部分需征税,设全月纳税所得额为x,x=全月总收入-800元,税率见下表:
|
级数 |
全月纳税所得额 |
税率 |
|
1 |
不超过500元部分 |
5% |
|
2 |
超过500元至2000部分 |
10% |
|
3 |
超过2000元至5000部分 |
15% |
|
… |
… |
… |
|
9 |
超过10000元部分 |
45% |
(1)某人1月份应缴纳此项税款26.78元,则他当月工资总收入介于( )
A、800~900元 B、8900~1200元 C、1200~1500元 D、1500~2800元
(2)若应纳税额为f(x),试用分段函数表示1~3级纳税额f(x)的计算公式:
(3)某人2002年10月份总收入3000元,试计算该人此月份应缴纳个人所得税多少元?
13、(综合2)已知定义域为[a,b]的函数y=f(x)的图象如图2-1-17所示,则y=f(|x|)的图象为( )
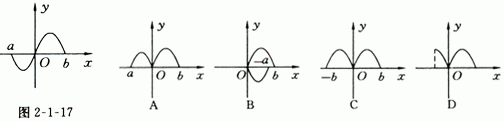
14、(综合1)若将函数y=f(x)的图象平移,使图象上的点(1,2)变为(2,2),则此图象平移后的解析式为( )
A、y=f(x-1) B、y=f(x)-1 C、y=f(x+1) D、y=f(x)+1
创新拓展
15、(综合1)已知函数y=f(x-1)的图象,通过怎样的图象变换可得到y=f(-x+2)的图象?
16、(创新应用)某学生离家去学校,由于怕迟到,所以一开始就跑步,等跑累了再走余下的路程,在下图中,纵轴表示离学校的距离,横轴表示出发后的时间,则图中四个图形中较符合该学生到校办法的是( )

17、(创新应用)如图2-1-18所示,动点P从边长为1的正方形ABCD的顶点A出发顺次经过B,C,D,再回到A,设x表示P点行程,y表示PA的长,求y关于x的函数关系式。
|