自主迁移

    1、某家报刊销售点从报社买进报纸的价格是每份0.35元，卖出的价格是每份0.50元，卖不掉的报纸还可以以每份0.08元的价格退回报社。在一个月（按30天计）里，有20天每天可卖出400份，其余10天每天只能卖出250份。设每天从报社买进的报纸的份数相同。则应该每天从报社买进多少份报纸，才能使每月所获得利润最大？并求出最大利润。

    2、假设国家收购某种家产品的价格是120元/担，其中征税标准为每100元征8元（叫做税率为8个百分点，即8%），计划可收购m万担。为了减轻农民负担，决定税率降低x个百分点。预计收购量可增加2x个百分点。

    （1）写出税收y（万元）与x的函数关系。

    （2）要使此项税收在税率调整后，不低于原计划的78%，试确定x的范围。

    3、某公司生产一种电子仪器的固定成本为20000元，每生产一台仪器需增加投入100元，已知总收益满足函数：

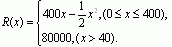
    （1）将利润表示为月产量的函数f（x）；

    （2）当月产量为何值时，公司所获利润最大？最大利润为多少元？（总收益=总成本+利润）

    4、某厂生产某种零件，每个零件的成本为40元，出厂单价为60元，该厂为鼓励销售商订购，决定当一次订购量超过100个时，每多订购一个，订购的全部零件的出厂单价降低0.02元，但实际出厂单位不能低于51元。

    （1）当一次订购量为多少时，零件的实际出厂单价恰为51元？

    （2）设一次订购量为x个，零件的实际出厂单价为P元，写出函数P=f（x）表达式；

    （3）当销售商一次订购500个零件时，该厂获得的利润是多少元？如果订购1000个，利润又是多少元？

    5、我国1999年至2002年国内生产总值（单位：万亿元）如下表所示：

    （1）画出（x，y）的散点图，近似地写出一个函数关系式；

    （2）利用得出的关系式检验表中未用数据；

    （3）利用得出的关系式预测2003年我国的国内生产总值。

    新课标梯度评价

    基础巩固

    1.（知能点1）一辆匀速行驶的火车90分钟行驶了180km，则这辆火车行驶的路程y（km）与时间t（h）之间的函数关系为（    ）

       A、y=2t                 B、y=120t

       C、y=2t（t≥0）         D、y=120t（t≥0）

    2.（知能点1）一等腰三角形的周长是20，则底边y是关于腰长x的函数，其解析式为（    ）

       A、y=20－2x（x≤10）

       B、y=20－2x（x＜10）

       C、y=20－2x（5≤x≤10）

       D、y=20－2x（5＜x＜10）

    3.（知能点2）用长度为24m的材料围成一矩形场地，并且中间加两道隔墙，要使矩形面积最大，则隔墙的长度就为（    ）

       A、3m                 B、4m

       C、6m                 D、12m

    4.（知能点2）将进货单价为80元的商品按90元一个售出时，能卖出400个，已知该商品每个涨价1元，其销售量就减少20个，为了赚得最大利润，售价应定为（    ）

       A、每个110元

       B、每个105元

       C、每个100元

       D、每个95元

    5.（综合）已知A、B两地相距150公里，某人开汽车以每小时60公里的速度从A地到B地，在B地停留一小时后再以每小时50公里的速度返回A地，把汽车离开A地的距离x表示为t的函数，表达式是（    ）

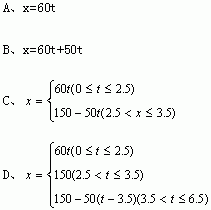
    6.（综合）《在华人民共和国个人所得税法》规定，公民全月工资、薪金所得不超过800的部分不必纳税，超过800元的部分为全月应纳税所得额，此项税款按下表分段累进计算：

    某人一月份应交纳此税款26.78元，则它的当月工资所得介于（    ）

        A、800～900元               B、900～1200元

        C、1200～1500元             D、1500～2800元

    7.（知能点1，2）某种产品市场产销量情况如图2-3-4所示，其中L₁表示产品各年年产量的变化规律；L₂表示产品各年的销售情况，下列叙述：

    （1）产品产量、销售量均以直线上升，仍可按原生产计划进行下去；

    （2）产品已经出现了供大于求的情况价格将趋跌；

    （3）产品的库存积压将越来越严重，应压缩产量或扩大销售量，你认为较合理的叙述是（    ）

        A、（1）（2）（3）              B、（1）（3）

        C、（2）                       D、（2）（3）

    8.（知能点2）某产品的成本y（万元）与产量x（台）之间的函数关系式是y=3000+20－0.1x²，x∈（0，240），若每台产品的售价为25万元，则生产者不亏本时（销售收入不小于总成本）的最低产量为（    ）

        A、100台                       B、120台

        C、150台                       D、180台

    能力培养

    9.（知能点1，2）某工厂八年来某种产品总产量c与时间t（年）的函数关系如图2-3-5，下列四种说法：

    ①前三年中产量增长速度越来越快；

    ②前三年中产量增长速度越来越慢；

    ③第三年后，这种产品停止生产；

    ④第三年后，年产量保持不变。

    其中说法正确的是       。

    10.（知能点2）用一根长为12m的铁丝弯折成一个矩形的铁框架，则能弯成的框架的最大面积是       。

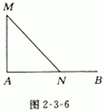
    11.（知能点2）如图2-3-6所示，大海中的两艘船，甲船在A处，乙船在A处正东50km的B处，现在甲船从A处以20km/h的速度向正北方向航行，同时乙船从B处以10km/h的速度向正西方航行，则经过       h后，两船相距最近。

    12.（综合）如图2-3-7，在边长为4的正方形ABCD的边上有一点P，沿折线BCDA由点B（起点）向点A（终点）运动，设点P运动的路程为x，△APB的面积为y。

    （1）求y与x的关系式；

    （2）画出y=f（x）的图象。

    13.（知能点2）某租凭公司拥有汽车100辆，当每辆车的月租金3000元时，可全部租出，当每辆车的月租金增加50元时，未租出的车将会增加1辆。租出的车每辆每月需要维护费150元，未租出的每辆每月需要维护费50元。

    （1）当每辆车的月租金定为3600元时，能租出多少辆车？

    （2）当每辆车的月租金定为多少元时，租凭公司的月收益最大？最大月收益是多少元？

    14.（知能点1）为了保护学生的视力，课桌椅的高度都是按一定的关系配套设计的，研究表明：假设课桌的高度为y cm，椅子的高度为x cm，则y应是x 的一次函数。下表列出两套符合条件的课桌椅的高度：

    （1）请你确定y与x的函数关系式（不必写出x的取值范围）；

    （2）现有一把高42.0cm的椅子和一张高78.2cm的课桌，它们是否配套？为什么？

    （1）把利润表示为年产量的函数；

    （2）年产量是多少时，工厂所得利润最大？

    （3）年产量是多少时，工厂才不亏本？

    16.（知能点2）某村计划建造一个室内面积为800m²的矩形蔬菜温室。在温室内，沿左、右两侧与后侧内墙各保留1m宽的通道，沿前侧内墙保留了3m宽的空地。当矩形温室的边长各为多少时，蔬菜的种植面积最大？最大种植面积是多少？

    创新拓展

    17.（数学与生活）某家庭今年一月份、二月份、三月份煤气用量支付费如下表所示：

    该市煤气收费的方法是：煤气费=基本费+超额费+保险费+，若每月用气量不超过最低限定A m³，只付基本费3元和每户每月的定额保险费C元，若用气量超过A m³时，超过部分每立方米（m³）付B元。又知保险费不超过5元，根据上面的表格求A、B、C。

    18.（多变题）通过研究学生的学习行为，心理学家发现，学生的接受能力依赖于老师引入概念和描述问题所用的时间。讲座开始时，学生的兴趣激增，中间有一段不太长的时间，学生的兴趣保持较理想的状态，随后学生的注意力开始分散。分析结果和实验表明，用f（x）表示学生掌握和接受概念的能力，x表示提出和讲授概念的时间（单位：分）可有以下的公式：

    （1）开讲后多少分钟，学生的接受能力最强？能维持多长时间？

    （2）开讲后5分钟与开讲后20分钟比较，学生的接受能力何时强一些？

    （3）一道数学难题，需要55的接受能力以及13分钟时间，老师能否及时在学生一直达到所需接受能力的状态下讲授完这道难题？

    参考答案：

    自主迁移

    1．解：设每天应从报社买x份，易份250≤x≤400.

    设每月利润为y元，则有

    y=0.5x×20+0.5×250×10+(x-250)×0.08×10-0.35×x×30

    =0.3x+1050，x∈[250，400].

    由于函数y=0.3x+1050在定义域上是增函数，所以当x=400时，y取最大值y_max=400×0.3+1050=1170(元)

    即每天应从报社买进400份报纸，获得的最大利润每月为1170元.

    2．解：(1)由于税收=总收入×税率，所以

    y=120×m×(1+2x%)×(8%-x%)×10⁴

    =-240m(x²+42x-400)(0＜x≤8).

    (2)要使税收在税率调整后不低于原计划的78%，则应有：-240m(x²+42x-400)≥120×m×10⁴×8%×78%，

    即x²+42x-88≤0，解得-44≤x≤2.

    又∵0＜x≤8，∴0＜x≤2.

    即x的范围是0＜x≤2.

    3．解：(1)设月产量为x台，则总成本为20000+100x，从而，

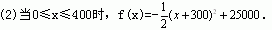
    ∴当x=300时，有最大值25000.

    当x＞400时，f(x)=60000-100x是减函数，

    f(x)＜60000-100×400＜25000.

    答：每月生产300台仪器时，利润最大，最大利润为25000元.

    因此，当一次订购量为550个时，每个零件的实际出厂价恰好为51元.

    (2)当0＜x≤100时，P=60；

    当100＜x＜550时，

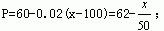
    当x≥550时，P=51.

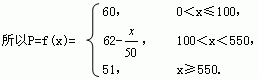
    (3)设销售商的一次订购量为x个时，工厂获得的利润为S元，

    当x=500时，S=6000；当x=1000时，S=11000.

    因此当销售商一次订购500个零件时，该厂利润是6000元；如果订购1000个，利润是11000元.

    5．解：(1)画散点图在此从略，从图形可以看出，四个点近似地落在一条直线上，设所求函数为y=kx+b.

    选择两点(0，8.2067)和(3，10.2398)代入，

    解方程组得k=0.6777，b=8.2067.

    因此所求函数关系式为y=f(x)=0.6777x+8.2067.

    (2)f(1)=0.6777×1+8.2067=8.8844，

    f(2)=0.6777×2+8.2067=9.5621.

    与表中相应函数值相比，误差不超过0.1(万亿元).

    (3)2003年，即x=4时，有

    f(4)=0.6777×4+8.2067=10.9175.

    即可以预测2003年国内生产总值约为10.9175万亿元.

    新课标梯度评价

    1．D    2. D    3. A    4. D    5. D    6. C    7. D    8. C

    9．②③     10. 9m²     11. 1

    (2)y=f(x)的图象如图所示.

    所以当x=4050时，f(x)最大，最大值是307050.即当每辆车的月租金为4050元时，租赁公司的月收益最大，最大月收益为307050元.

    14．解：(1)依题意，由于课桌高度y是椅子高度x的一次函数，故可设y=ax+b，将给出的符合条件的两套课桌椅的高度代入上述函数关系式，得

    所以y与x的函数关系式是y=1.6x+11.

    (2)将x=42代入(1)中的函数解析式得y=1.6×42+11=78.2，因此给出的这套课桌椅是配套的.

    15．解：(1)当x≤5时，产品能全部售出；当x＞5时，只能售出5百台，故利润函数为L(x)=R(x)-C(x)

    当x=4.75时，得L(x)_max=10.78125(万元).

    当x＞5时，L(x)＜12-1.25=10.75(万元).

    ∴生产475台时利润最大.

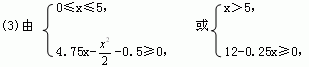
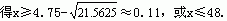
    ∴产品年产量在11台到4800台时，工厂不亏本.

    16．解：设矩形温室的左侧边长为am，后侧边长为bm，则

    ab=800，于是蔬菜的种植面积为

    答：当矩形温室的左侧边长为40m，后侧边长为20m时，蔬菜的种植面积最大，最大种植面积是648m².

    17．解：设每月煤矿气用量为xm³，支付费用为y元，根据题设条件，得

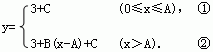
    由0≤C≤5，得3+C≤8.从表格中看出此家庭二、三月份的费用均大于8，故用气量25m³，35m³均大于最低限度Am³.所以，将x=25，x=35分别代入②，得

    再分析一月份的煤气用量是否超过最低限度，不妨设A＜4，将x=4代入②，得

    3+0.5[4-(2C+3)]+C=4，并由此得3.5=4，矛盾.

    所以A≥4，即一月份付费方式为①.

    所以3+C=4，即C=1.

    从而A=5，B=0.5，C=1.

    18．解：(1)当0＜x≤10时，

    f(x)=-0.1x²+2.6x+43=-0.1(x-13)²+59.9，

    故f(x)递增，最大值为

    f(10)=-0.1x²+2.6x+43

    显然，当16＜x≤30时，f(x)递减.

    f(x)＜-3×16+107=59.

    因此，开讲后10分钟，学生达到最强的接受能力(值为59)，并维持6分钟.

    (2)f(5)=-0.1×(5-13)²+59.9=59.9-6.4=53.5，

    f(20)=-3×20+107=47＜53.5，

    因此开讲后5分钟学生的接受能力比开讲后20分钟强一些.

    (3)当0＜x≤10时，令f(x)=55，则

    -0.1×(x-13)²=-4.9，(x-13)²=49，

    所以x=20或6，但0＜x≤10.故x=6.

    当16＜x≤30时，令f(x)=55，则
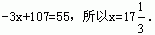
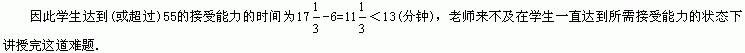