|
集合之间的关系
(一)重点知识理解与简单应用
知能点1 子集概念的理解自主迁移
1.下列问题中,正确的个数是( )
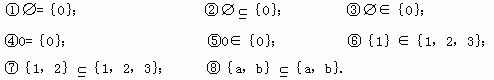
A.1 B.2 C.3 D.4
2.集合{0}与 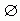 的关系是( ) 的关系是( )

知能点2 子集概念的简单应用
3.判断下列各组中两集合的关系:
(1)P={x|x=2n,n∈Z},Q={x|x=4n,n∈Z};
(2)P={x|x=2n,n∈Z},Q={x|x=2(n-1),n∈Z};
(3)P={x|x=2n-1,n∈N+},Q={x|x=2n+1,n∈N+};
(4)P={x|x= x2-x=0},

4.设集合A={x| x2+4x=0},B={x| x2+2(a+1)x+a2-1=0,a∈R},若B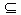 A,求实数a的值. A,求实数a的值.
5.若集合A={x2+x-6=0},B={x| mx+1=0},且B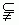 A,求m的值. A,求m的值.
知能点3子集个数的求法
6.写出集合A={p,q,r,s}的所有子集.
(二)学科内综合
综合1 利用集合与函数、不等式、方程的关系,求字母参数问题
7.已知A={x|x<3},B={x| x<a}.
(1)若B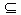 A,求a的取值范围; A,求a的取值范围;
(2)若A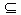 B,求a的取值范围. B,求a的取值范围.
8.若集合A={x|-2≤x≤5},B={x| m+1≤x≤2m-1},且B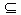 A,求由m的值组成的集合. A,求由m的值组成的集合.
9.(学科与生活)小明一家有爷爷、奶奶、爸爸、妈妈及小明五口人.
(1)写出小明家的人组成的集合A,爷爷、奶奶组成的集合B,小明和爸妈组成的集合C;
(2)试用韦恩图表示A与B,A与C,B与C之间的关系;
(3)写出A、B、C中的满足子集关系的所有情况.
综合3 多个集合的包含关系中的子集个数
10.已知集合M满足{1,2} M {1,2,3,4,5},写出集合M.
(三)创新拓展实践
11.(开放题)一位渔民非常喜欢数学,但它怎么也想不明白集合的意义,于是他请教数学家,“尊敬的先生,请你告诉我,集合是什么?”我们知道,集合是不定义的概念,数学家很难回答那位渔民,有一天,他来到渔民的船上,看到渔民撒下鱼网,轻轻一拉,许多鱼虾在网中跳动.
数学家非常激动,高兴地告诉渔民:“这就是集合.”
你能理解数学家的话吗?
新课标梯度评价
基础巩固
1.(知能点1)下列选项正确的是( )
A.{1,2}={2,1} B.0∈{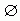 } C. } C.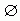 ={0} D. ={0} D.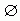  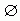
2.(知能点1)设M={0,1},N={x|x M},M与N的关系是( )
A.M∈N B.N∈M C.M N D.M=N
3.(知能点1)在以下六个写法中:
①{0}∈{0,1}; ②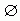 {0}; ③{0,1,-1} {-1,0,1}; {0}; ③{0,1,-1} {-1,0,1};
④0∈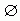 ; ⑤Z∈{全体整数}; ⑥{(0,0)}={0}. ; ⑤Z∈{全体整数}; ⑥{(0,0)}={0}.
错误写法的个数是 。
4.(知能点2)已知A={x|x<1或x>2},B={x|4x+a<0},当B A时,求实数a的取值范围.
5.(知能点2)设集合A={x,x2,xy},B={1,x,y},且A=B,求实数x,y的值.
6.(知能点3)已知集合A={x|x2=x,x∈R},满足条件B A的所有集合B的个数为( )
A.1 B.2 C.3 D.4
7.(知能点3)集合M={1,2,3,4,5}的子集个数为( )
A.32 B.31 C.16 D.15
能力培养
8.(综合1)已知A={x|x2+px+q=x},B={x|(x-1)2+p(x-1)+q= x+1},当A={2}时,求集合B.
9.(创新题)已知集合A={(x,y)|y=-x2+mx-1},B={(x,y)|x+y=3,0≤x≤3}若集合A与集合B有且只有一个公共元素,求实数m的取值范围.
10.(综合1)设集合A={x|x是菱形},B={x|x是平行四边形},C={x|x是正方形},指出A、B、C之间的关系?
11.(综合2)1-2-2中,A、B、C表示集合,说明他们之间的包含关系?
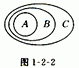
12.(综合1)集合{小明,小亮,小华}的子集共有( )
A.5个 B.6个 C.7个 D.8个
13.(新情景题)小明有2张卡片,小华有5张卡片,小亮想把小明的卡片全部拿来,并从小华的5张卡片中拿出部分(不全要,也不不要),问小亮有多少种不同的拿法(拿到不同的卡片记为不同情况)?
14.(探究题)填表:
|
集合 |
集合中元素的个数 |
子集的个数 |
|
{a} |
1 |
|
|
{a,b} |
2 |
|
|
{a,b,c} |
3 |
|
|
{a,b,c,d} |
4 |
|
|
{a,b,c,d,e} |
5 |
|
如果一个集合有n个元素,你能计算出它们所有子集的个数公式吗?

|