|
数学高考模拟试题(2)
第Ⅰ卷(选择题,共60分)
一、选择题:本大题共12小题;每小题5分,共60分.在每小题给出的四个选项中,有且只有一项是符合题目要求的.
(1)与向量 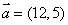 平行的单位向量为( )
平行的单位向量为( )
A. 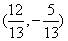 B.
B. 
C. 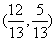 或
或  D.
D. 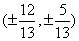
(2)函数 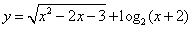 的定义域为( )
的定义域为( )
A.. 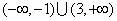 B.
B. 
C. 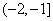 D.
D. 
(3)某地区高中分三类:A类校共有学生4000人,B类校共有学生2000人,C类校共有学生3000人。现欲抽样分析某次考试的情况,若抽取900份试卷进行分析,则从A类校抽取的试卷份数应为 ( )
A.450份 B.400份 C.300份 D.200份
(4)已知直线m、n和平面  ,则m∥n的一个必要条件是( )
,则m∥n的一个必要条件是( )
A.m∥  ,n∥
,n∥  B.m⊥
B.m⊥  ,n⊥
,n⊥ 
C.m∥  ,n
,n 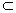
 D.m、n与
D.m、n与  成等角
成等角
(5)若正数 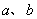 满足
满足 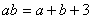 ,则
,则 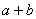 的取值范围是( )
的取值范围是( )
A. 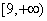 B.
B. 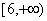 C.
C. 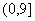 D.
D. 
(6)设双曲线 
 的实轴长、虚轴长、焦距成等比数列,则双曲线的离心率为( )
的实轴长、虚轴长、焦距成等比数列,则双曲线的离心率为( )
A. 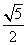 B.
B. 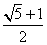 C.
C. 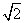 D.
D. 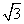
(7)若函数y=f(x) (xÎR)满足f(x 2)=f(x),且xÎ(-1,1]时,f(x)=|x|.则函数y=f(x)的图象与函数y=log4|x|的图象的交点的个数为( )
A.3 B.4 C.6 D.8
(8)已知点  是抛物线
是抛物线  上的动点,点
上的动点,点  在
在  轴上的射影是
轴上的射影是 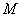 ,点
,点 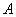 的坐标是
的坐标是  ,则
,则  的最小值是( )
的最小值是( )
A. 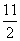 B.4
B.4  C.
C.  D.5
D.5
(9)已知函数 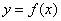 的图象与函数
的图象与函数 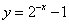 的图象关于
的图象关于
直线 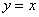 对称,则
对称,则 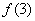 的值为 ( )
的值为 ( )
A.1 B. 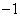 C.2 D.
C.2 D. 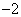
(10)能够使得圆  上恰有两个点到直线
上恰有两个点到直线 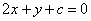 距离等于1的
距离等于1的  的一个值为( )
的一个值为( )
A.2 B. 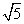 C.3 D.
C.3 D. 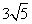
(11)关于x的不等式ax-b>0的解集是(1, ∞),则关于x的不等式  的解集是( )
的解集是( )
A.(-∞,-1)∪(2, ∞) B.(-1,2) C.(1,2) D.(-∞,1)∪(2, ∞)
(12)由0,1,2,…,9这十个数字组成的、无重复数字的四位数中,个位数字与百位数字之差的绝对值等于8的个数为( )
A.180 B.196 C.210 D.224
第Ⅱ卷(非选择题,共90分)
二、填空题:本大题共4小题;每小题4分,共16分.把答案填在题中横线上.
 (13)如图,已知点 (13)如图,已知点 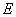 是棱长为2的正方体
是棱长为2的正方体  的棱
的棱 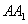 的中点,则点
的中点,则点 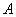 到平面
到平面 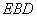 的距离等于_____________.
的距离等于_____________.
(14)若 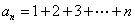 ,则数列
,则数列 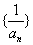 的前
的前  项和
项和  _____________.
_____________.
(15)已知 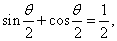 则
则 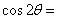 .
.
(16)有两个向量 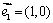 ,
,  ,今有动点
,今有动点  ,从
,从  开始沿着与向量
开始沿着与向量  相同的方向作匀速直线运动,速度为
相同的方向作匀速直线运动,速度为 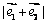 ;另一动点
;另一动点 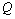 ,从
,从 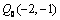 开始沿着与向量
开始沿着与向量 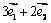 相同的方向作匀速直线运动,速度为
相同的方向作匀速直线运动,速度为 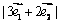 .设
.设  、
、 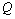 在时刻
在时刻  秒时分别在
秒时分别在  、
、 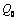 处,则当
处,则当  时,
时, 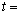 秒.
秒.
三、解答题:本大题6小题,共74分.解答应写出文字说明,证实过程或演算步骤.
(17)(本小题满分12分)
某厂生产的A产品按每盒10件进行包装,每盒产品均需检验合格后方可出厂.质检办法规定:从每盒10件A产品中任抽4件进行检验,若次品数不超过1件,就认为该盒产品合格;否则,就认为该盒产品不合格.已知某盒A产品中有2件次品.
(1)求该盒产品被检验合格的概率;
(2)若对该盒产品分别进行两次检验,求两次检验得出的结果不一致的概率.
(18)(本小题满分12分)
已知偶函数f(x)=cosqsinx-sin(x-q) (tanq-2)sinx-sinq的最小值是0,求f(x)的最大值及此时x的集合.
(19) (本小题满分12分)
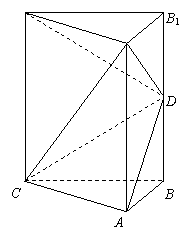
如图,直三棱柱 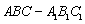 中,
中, 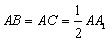 ,
, 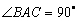 ,
, 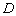 为棱
为棱 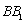 的中点.
的中点.
 (Ⅰ)求异面直线
(Ⅰ)求异面直线 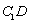 与
与  所成的角;
所成的角;
(Ⅱ)求证:平面  平面
平面 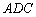 .
.
(20) (本小题满分12分)
已知二次函数f(x)满足:①在x=1时有极值; ②图象过点(0,-3),且在该点处的切线与直线2x y=0平行.
(I)求f(x)的解析式;
(II)求函数g(x)=f(x2)的单调递增区间。
(21) (本小题满分12分)
等差数列 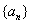 中,
中, 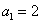 ,公差
,公差 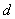 是自然数,等比数列
是自然数,等比数列 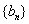 中,
中, 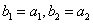 .
.
(1)试找出一个 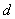 的值,使
的值,使 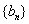 的所有项都是
的所有项都是 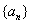 中的项;再找出一个
中的项;再找出一个 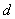 的值,使
的值,使 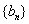 的项不都是
的项不都是 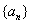 中的项(不必证实);
中的项(不必证实);
(Ⅱ)判定  时,是否
时,是否 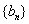 所有的项都是
所有的项都是 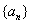 中的项, 并证实你的结论;
中的项, 并证实你的结论;
(Ⅲ)探索当且仅当 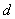 取怎样的自然数时,
取怎样的自然数时, 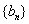 的所有项都是
的所有项都是 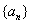 中的项,并说明理由.
中的项,并说明理由.
(22)(本小题满分14分)
如图,已知过点 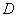
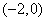 的直线
的直线 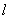 与椭圆
与椭圆  交于不同的两点
交于不同的两点 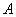 、
、 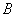 ,点
,点 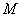 是
是  弦 弦 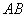 的中点.
的中点.
(Ⅰ)若  ,求点
,求点  的轨迹方程;
的轨迹方程;
(Ⅱ)求 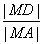 的取值范围.
的取值范围.
05年数学高考模拟试题(2)参考解答及点评
一、选择题:每小题5分,满分60分.(注重:选择与填空解析及点评见最后)
(1)C (2)D (3)B (4)D (5)B (6) B (7)C (8)C (9)D (10)C (11)A (12)C
二、填空题:每小题4分,满分16分.
(13) 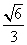 ; (14)
; (14) 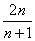 ; (15)
; (15) 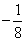 ; (16)2.
; (16)2.
三、解答题
(17)(本小题满分12分)
解析: (1)从该盒10件产品中任抽4件,有等可能的结果数为 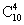 种,其中次品数不超过1件有
种,其中次品数不超过1件有 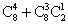 种,被检验认为是合格的概率为
种,被检验认为是合格的概率为 
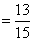 .
.
(2)两次检验是相互独立的,可视为独立重复试验,因两次检验得出该盒产品合格的概率均为  , 故“两次检验得出的结果不一致”即两次检验中恰有一次是合格的概率为
, 故“两次检验得出的结果不一致”即两次检验中恰有一次是合格的概率为
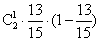
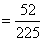 .
.
答:该盒产品被检验认为是合格的概率为  ;两次检验得出的结果不一致的概率为
;两次检验得出的结果不一致的概率为 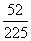 .
.
点评:本题考查了等可能性事件与独立重复事件的概率。
(18)(本小题满分12分)
解析:f(x)=cosqsinx-(sinxcosq-cosxsinq) (tanq-2)sinx-sinq
=sinqcosx (tanq-2)sinx-sinq.
因为f(x)是偶函数,所以对任意xÎR,都有f(-x)=f(x),
即sinqcos(-x) (tanq-2)sin(-x)-sinq=sinqcosx (tanq-2)sinx-sinq,
即(tanq-2)sinx=0,所以tanq=2.
由  解得
解得  或
或 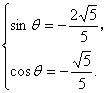
此时,f(x)=sinq(cosx-1).
当sinq=  时,f(x)=
时,f(x)=  (cosx-1)最大值为0,不合题意最小值为0,舍去;
(cosx-1)最大值为0,不合题意最小值为0,舍去;
当sinq= 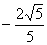 时,f(x)=
时,f(x)= 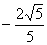 (cosx-1)最小值为0,
(cosx-1)最小值为0,
 当cosx=-1时,f(x)有最大值为 当cosx=-1时,f(x)有最大值为  ,自变量x的集合为{x|x=2kp p,kÎZ}.
,自变量x的集合为{x|x=2kp p,kÎZ}.
点评:本题将函数性质应用于三角函数中。
(19)(本小题满分12分)
解法一:
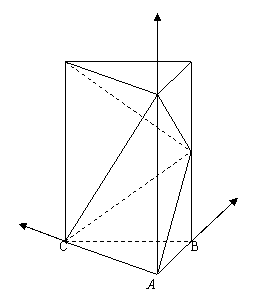
(Ⅰ)建立如图所示的空间直角坐标系.
设 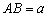 ,
,
则 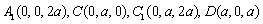 ,
,
于是 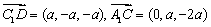 .
.
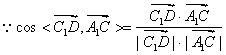
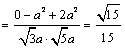 ,
,
 异面直线
异面直线 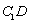 与
与  所成的角为
所成的角为 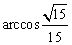 .
.
(Ⅱ) 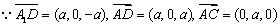 ,
,
 . 则
. 则 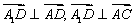 .
.
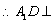 平面
平面  . 又
. 又  平面
平面  ,
,
 平面
平面  平面
平面 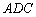 .
.
解法二:
(Ⅰ)连结 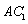 交
交  于点
于点 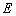 ,取
,取 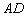 中点
中点 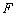 ,连结
,连结 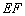 ,则
,则 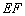 ∥
∥ 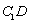 .
.
 ∴直线 ∴直线 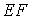 与
与 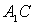 所成的角就是异面直线
所成的角就是异面直线 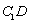 与
与  所成的角.
所成的角.
设 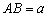 ,
,
则 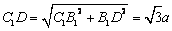 ,
,
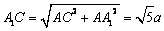 .
.
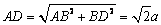 .
.
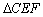 中,
中,  ,
, 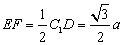 ,
,
直三棱柱中, 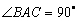 ,则
,则 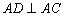 .
.
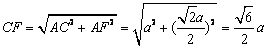 .
.
 ,
,
 异面直线
异面直线 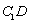 与
与  所成的角为
所成的角为 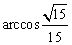 .
.
(Ⅱ)直三棱柱中, 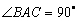 ,
, 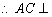 平面
平面  .
.
则  .
.
又 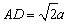 ,
, 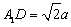 ,
, 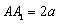 ,
,
则  ,
,  于是
于是 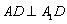 .
.
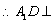 平面
平面  . 又
. 又  平面
平面  ,
,
 平面
平面  平面
平面 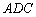 .
.
点评:两种思路,从两个不同角度研究了直三棱柱背景下线面位置关系与数量关系。
(20)(本小题满分12分)
解析:(I)设f(x)=ax2 bx c,则f ¢(x)=2ax b.
由题设可得:  即
即 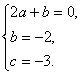
解得 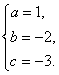 所以f(x)=x2-2x-3.
所以f(x)=x2-2x-3.
(II)g(x)=f(x2)=x4-2x2-3,g ¢(x)=4x3-4x=4x(x-1)(x 1).
列表: |
x |
(-∞,-1) |
-1 |
(-1,0) |
0 |
(0,1) |
1 |
(1, ∞) | |
f¢(x) |
- |
0 |
|
0 |
- |
0 |
| |
f(x) |
↘ |
|
↗ |
|
↘ |
|
↗ | |