|
高考文科数学第二次摸底考试试卷
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分, 满分150分,考试时间120分钟。
第Ⅰ卷(选择题,共60分)
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.下列函数中没有反函数的是 ( )
A.y=2x B.y=x2 C. 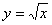 D.
D. 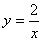
2.命题:“若 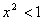 ,则
,则 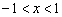 ”的逆否命题是 ( )
”的逆否命题是 ( )
A.若 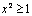 ,则
,则 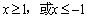 B.若
B.若 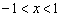 ,则
,则 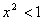
C.若 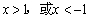 ,则
,则 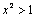 D.若
D.若 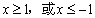 ,则
,则 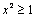
3.设M和N是两个集合,定义集合M-N= 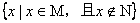 ,假如
,假如 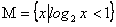 ,
,  那么M-N等于 ( )
那么M-N等于 ( )
A.{x|0<x<1} B.{x|0<x≤1} C.{x|1≤x<2} D.{x|2≤x<3}
4.采取简单随机抽样,从含有6个个体的总体中抽取一个容量为3的样本,个体a前两次未被抽到,第三次被抽到的概率为 ( )
A. 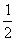 B.
B. 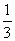 C.
C. 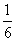 D.
D. 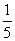
5.在等差数列{an}中,已知a1= 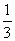 ,
,  ,那么a3等于 ( )
,那么a3等于 ( )
A.4 B.5 C.6 D.7
6.设函数f(x)= 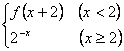 ,则f(-3)的值为 ( )
,则f(-3)的值为 ( )
A.2 B.8 C. 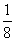 D.
D. 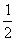
7.已知f(x)是定义在R上的奇函数,且为周期函数,若它的最小正周期为T,则f(- 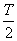 )= ( )
)= ( )
A.0 B. 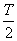 C.T D.
C.T D. 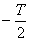
8.已知正三棱柱ABC-A1B1C1的侧棱长与底面边长相等,则AB1与侧面ACC1A1所成角的正弦等于 ( )
A. 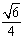 B.
B. 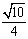 C.
C.  D.
D. 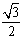
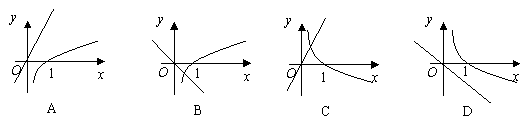 9.当a>1时,函数 9.当a>1时,函数 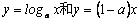 的图象只可能是 ( )
的图象只可能是 ( )
10.曲线f(x)=x3 x-2在其上一点P0处的切线平行于直线y=4x-1,则P0点的坐标是( )
A.(-1,-4) B.(1,0) C.(-1,0) D.(1,0)或(-1,-4)
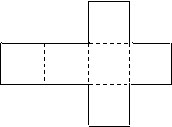 11.如图是一个正方体纸盒子的展开图,把1、-1、2、 11.如图是一个正方体纸盒子的展开图,把1、-1、2、
-2、3、-3分别填入六个正方形,使得按虚线折
成正方体后,相对面上的两个数的绝对值相等,求
不同填法的种数为 ( )
A.3 B.6
C.24 D.48
12.设函数f(x),对任意的实数x、y,有f(x y)=f(x) f(y),
且当x>0时,f(x)<0,则f(x)在区间 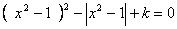 上 ( )
上 ( )
A.有最大值f(a) B.有最小值f(a)
C.有最大值 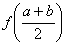 D.有最小值
D.有最小值 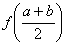
第Ⅱ卷(非选择题,共90分)
二、填空题(本大题共4小题,每小题4分,共16分.)
13.曲线 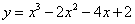 的单调递增区间是 .
的单调递增区间是 .
14. 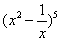 展开式中
展开式中 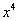 的系数是 .(用数字作答)
的系数是 .(用数字作答)
15.一个容量为20的样本,数据的分组及各组的频数如下: 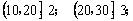
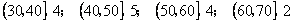 .则样本在区间
.则样本在区间 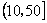 上的频率为 .
上的频率为 .
16.关于x的方程 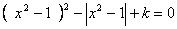 给出下列四个命题:
给出下列四个命题:
①存在实数k,使方程恰好有2个不同的实数根;
②存在实数k,使方程恰好有4个不同的实数根;
③存在实数k,使方程恰好有5个不同的实数根;
④存在实数k,使方程恰好有8个不同的实数根;
其中是真命题的有 .(填序号)
三、解答题(本大题共6小题,共74分.解答应写出必要的文字说明、证实过程或演算步骤.)
17.(12分)已知集合A= 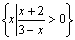 ,B=
,B= 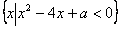 ,若AÇB=B,求a的取值范围.
,若AÇB=B,求a的取值范围.
18.(12分)某人居住在A处,预备开车到B处上班.若各路段发生堵车都是相互独立的,且
同一路段发生堵车最多只有一次,发生堵车的概率如图(例如: 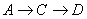 QUOTE
QUOTE  算作两段:路段AC发生堵车的概率为 算作两段:路段AC发生堵车的概率为 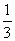 ,路段CD发生堵车的概率为
,路段CD发生堵车的概率为 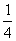 )。
)。
(1)请你为其选择一条由A到B的路线,使不堵车的概率最大;
(2)求路线  QUOTE
QUOTE 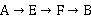 中堵车不多于2次的概率. 中堵车不多于2次的概率.
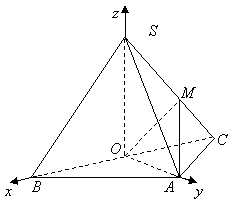
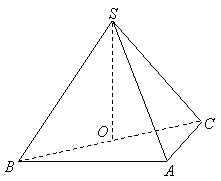 19.(12分) 如图,在三棱锥 19.(12分) 如图,在三棱锥 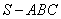 中,侧面
中,侧面 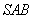 与侧面
与侧面 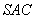 均为等边三角形,
均为等边三角形, 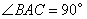 ,
, 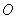 为
为 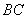 中点.
中点.
(Ⅰ)证实: 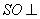 平面
平面 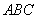 ;
;
(Ⅱ)求二面角 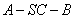 的余弦值.
的余弦值.
20.(12分)已知函数 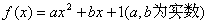 ,
, 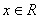 .
. 
(1)若 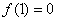 ,且函数
,且函数 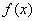 的值域为
的值域为 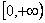 ,求
,求 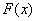 的表达式;
的表达式;
(2)在(1)的条件下,当 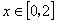 时,
时, 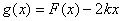 是单调函数,求实数
是单调函数,求实数 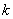 的取值范围.
的取值范围.
21.(12分)数列 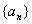 的前
的前 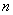 项和记作
项和记作  ,满足
,满足 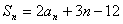 ,
, 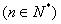 .
.
(1)证实数列 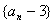 为等比数列;并求出数列
为等比数列;并求出数列 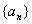 的通项公式.
的通项公式.
(2)记  ,数列
,数列 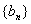 的前
的前 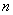 项和为
项和为 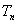 ,求
,求 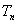 .
.
22.(14分)已知函数 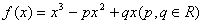 的图像与
的图像与 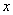 轴切于点
轴切于点 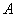 (1,0).
(1,0).
(1)求函数 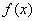 的解析式;
的解析式;
(2)若对于任意的 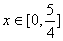 ,方程
,方程 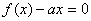 恰有三个不同的实根,求实数
恰有三个不同的实根,求实数 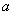 的范围.
的范围.
参考答案
1—5 BDBCA 6—10 CAABD 11—12 DA
13. 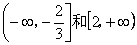 14.10 15.0.7 16. ①②③④
14.10 15.0.7 16. ①②③④
17.(12分)解: 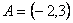 ,由题意知
,由题意知 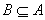 ,
,
(1)B=f时,  ;
;
(2)B≠f时,∵ 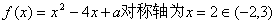 ,
,
∴只须满足 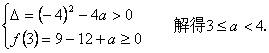
综上所述:a的取值范围是 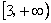 .
.
18.(12分)解:记AEFB表示  不堵车,其它类似.
不堵车,其它类似.
(1)P(AEFB)= 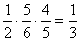 , P(ACDB)=
, P(ACDB)= 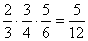 ,P(ACFB)=
,P(ACFB)= 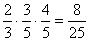 ,
,
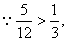
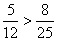 ,
, 
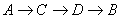 为最佳路线.
为最佳路线.
(2)堵车3次的概率 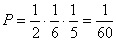 ,
,
堵车不多于2次的概率 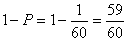 .
.
19.(12分)证实:(Ⅰ)由题设 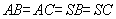
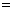
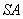 ,连结
,连结 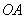 ,
,
所以, 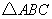 为等腰直角三角形,
为等腰直角三角形,
所以 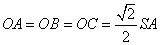 ,且
,且 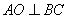 ,又
,又 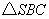 为等腰三角形,
为等腰三角形,
故 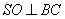 ,且
,且 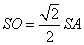 ,从而OA2 SO2=SA2.∴
,从而OA2 SO2=SA2.∴ 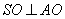 .
.
又 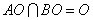 .
.
所以 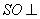 平面
平面 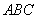 .
.
(Ⅱ)解法一:
取 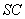 中点
中点  ,连结
,连结 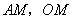 ,由(Ⅰ)知
,由(Ⅰ)知 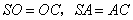 ,
,
得  .
. 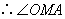 为二面角
为二面角 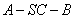 的平面角.
的平面角.
由 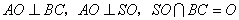 得
得 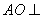 平面
平面 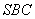 .
.
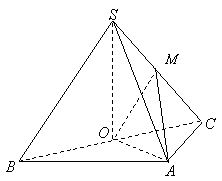 所以 所以 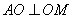 ,又
,又 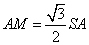 ,
,
故 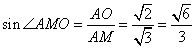 .
.
所以二面角 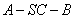 的余弦值为
的余弦值为 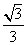 .
.
解法二:
以 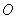 为坐标原点,射线
为坐标原点,射线 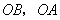 分别为
分别为 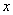 轴、
轴、  轴的正半轴,建立如图的空间直角坐标系
轴的正半轴,建立如图的空间直角坐标系  .设
.设  ,则
,则  .
.
 的中点
的中点 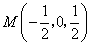 ,
,  .
.
 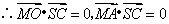 .
.
故 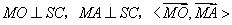 等于
等于
二面角 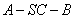 的平面角.
的平面角.
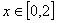 ,
,
所以二面角 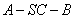 的余弦值为
的余弦值为 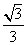 .
.
20.(12)解:(1)已知 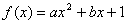 , 由
, 由 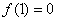 ,得
,得
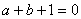 ,
, 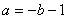 . ①
. ①
又 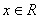 时,值域为
时,值域为 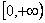 ,得
,得
 ②
②
①、②联立,解得 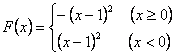 .
.
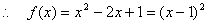 ,
,
∴ 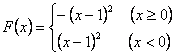
(2)由(1),当 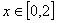 时,
时,
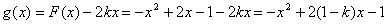
其对称轴为直线 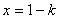 ,若
,若 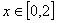 时
时 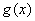 为单调函数,则
为单调函数,则
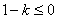 , 或
, 或 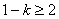 .
.
解得 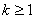 , 或
, 或 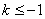 .
.
21.(12分)解:(1) 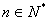 时,
时, 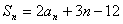 ………… = 1 \* GB3 ①
………… = 1 \* GB3 ①
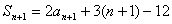 ,………… = 2 \* GB3 ②
,………… = 2 \* GB3 ②
= 2 \* GB3 ②— = 1 \* GB3 ①得: 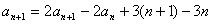 ,即
,即 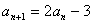 ,
,
可变形为 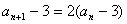 ,亦即
,亦即 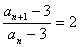 ………………………………3分
………………………………3分
所以数列 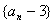 是以
是以 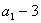 为首项,2为公比的等比数列. ……………………4分
为首项,2为公比的等比数列. ……………………4分
在 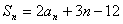 中,令
中,令 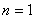 ,可求得
,可求得 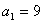 . ……………………5分
. ……………………5分
所以 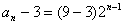 ,即
,即 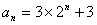 ,
, 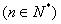 ……………………7分
……………………7分
(2)∵bn=nan=3n 3n×2n,
∴ 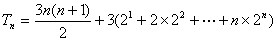 ,………………………………8分
,………………………………8分
令 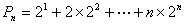 ,
,
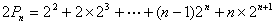 ,上二式作差,
,上二式作差,
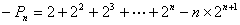
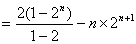 ,
,
所以 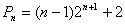 . ………………………………………………10分
. ………………………………………………10分
所以 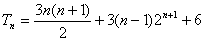 . ……………………………………………12分
. ……………………………………………12分
22.(14分)解:(1) 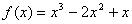 .
.
(2)解法(一):
由 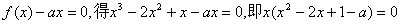 .
.
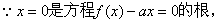
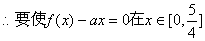 有三个不同的根,只需使
有三个不同的根,只需使  在
在 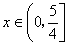 有不同的两个实根.
有不同的两个实根.
令 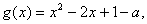 则只需
则只需 
解法(二)利用数形结合的思想;
解法(三) 由  得
得 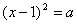 ,得
,得 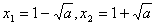 .
.
所以,只需 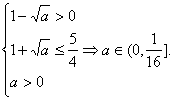
解法(四)分离系数法: 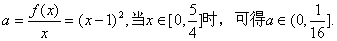
|