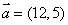推荐文章
- 08高考数学函数方程思想
- 08高考数学函数图象与图象变换复习
- 08高考数学二三轮复习技巧练习
- 08高考数学专题训练5
- 08高考数学专题训练13
- 08高考数学不等式的综合应用
- 08高考数学三角函数复习训练
- 08高考数学三个“二次”及关系试题
- 08高中毕业班文科数学第一次模拟考试
- 08汕头市高考文科数学模拟试题
- 08年高考理科教学第一次统一质量检测
- 08年高考文科数学模拟考试题卷
08届高考文科数学月考试题卷
08届高考文科数学月考试题卷(三)
数学(文科)试题卷
一、选择题(每题只有一个选择满足要求,每小题5分,共50分)
1.设集合 ![]()
A. ![]()
![]()
![]()
![]()
2.已知向量 ![]()
![]()
![]()
![]()
A. ![]()
![]()
![]()
3.函数 ![]()
![]()
A.2 B.
4.设 ![]()
![]()
![]()
![]()
![]()
![]()
![]()
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
5.已知函数 ![]()
![]()
![]()
A.关于点 ![]()
![]()
C.关于点 ![]()
![]()
6.一个四边形的四个内角成等差数列,最小角为 ![]()
A. ![]()
![]()
![]()
![]()
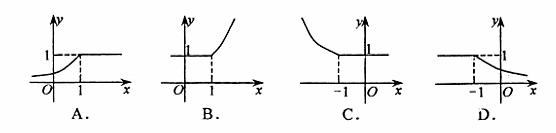
7.函数 ![]()
A. ![]()
![]()
![]()
![]()
8.函数 ![]()
A. ![]()
![]()
![]()
![]()
9.假如我们定义一种运算: ![]()
![]()
![]()
![]()
10.4只笔与5本书的价格之和小于22元,而6只笔与3本书的价格之和大于24元,则2只笔与3本书的价格比较( )
A.2只笔贵 B.3本书贵 C.二者相同 D.无法确定
二、填空题(每小题5分,共20分)
11.函数 ![]()
12.定义在R上的奇函数f(x)满足 ![]()
![]()
![]()
13.设 ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
 (从下列2题中选做一题,若全做的按前一题记分)
(从下列2题中选做一题,若全做的按前一题记分)
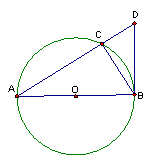
14.已知圆O直径为10,AB是圆O的直径,C为圆O上一点,且BC=6,过点B的圆O的切线交AC延长线于点D,则DA=_______________;
15.曲线 ![]()
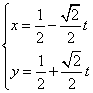
三、解答题(共80分)
16、(本题12分)已知数列 ![]()
![]()
![]()
![]()
![]()
( = 1 \* ROMAN I) 求数列 ![]()
![]()
![]()
![]()
( = 2 \* ROMAN II) 若数列 ![]()
![]()
![]()
![]()
![]()
![]()
![]()
17、(本题12分)在 ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
( = 1 \* ROMAN I)求 ![]()
( = 2 \* ROMAN II)求 ![]()
18、(本题14分)某公司要将一批不易存放的蔬菜从A地运到B 地,有汽车、火车两种运输工具可供选择,两种运输工具的主要参考数据如下表:
|
运输工具 |
途中速度 (km/h) |
途中费用 (元/km) |
装卸时间 (h) |
装卸费用 (元) |
|
汽车 |
50 |
8 |
2 |
1000 |
|
火车 |
100 |
4 |
4 |
2000 |
若这批蔬菜在运输过程(含装卸时间)中损耗为300元/h,设A、B 两地距离为 ![]()
( = 1 \* ROMAN I)设采用汽车与火车运输的总费用分别为 ![]()
![]()
![]()
![]()
( = 2 \* ROMAN II)试根据A、B两地距离大小比较采用哪种运输工具比较好(即运输总费用最小).
(注:总费用=途中费用+装卸费用+损耗费用)
19、(本题14分)已知函数 ![]()
( = 1 \* ROMAN I)若 ![]()
![]()
![]()
( = 2 \* ROMAN II)若 ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
20、(本题14分)已知 ![]()
![]()
( = 1 \* ROMAN I)求实数 ![]()
( = 2 \* ROMAN II)记实数 ![]()
![]()
![]()
![]()
= 1 \* GB3 ①求 ![]()
= 2 \* GB3 ②试问:是否存在实数m,使得不等式 ![]()
![]()
![]()
21、(本题14分)设 ![]()
![]()
![]()
![]()
![]()
![]()
![]()
( = 1 \* ROMAN I)在使得 ![]()
![]()
![]()
![]()
( = 2 \* ROMAN II)求 ![]()
![]()
( = 3 \* ROMAN III)记函数 ![]()
![]()
![]()
![]()
![]()
![]() 数学(文科)答题卷
数学(文科)答题卷
|
姓名:________________班级:________________学号:__________________ |
 第二部分 非选择题答题卷
第二部分 非选择题答题卷
二、填空题(每小题5分,共20分):
11.___________________;12.___________;13.___________________________________;
14.___________________;15.___________;
三、解答题:(共80分,要求写出解答过程)
 16.(本小题满分12分)
16.(本小题满分12分)
17.(本小题满分12分)

18.(本小题满分14分)

19.(本小题满分14分)

20.(本小题满分14分)
|
姓名:________________班级:________________学号:__________________ |


21.(本小题满分14分)

数学(文科)答案
一、选择题
1.B 2.A 3.C 4.A 5.B 6。A 7.B 8.D 9.B 10.A
10.设每支笔x元,每本书y元,有 ![]()
![]()
![]()
![]()
二、填空题:
11.(-1,1) 12. -1 13. ![]()
![]()
三、解答题:
16解:( = 1 \* ROMAN I)设数列 ![]()
![]()
由题意可知: 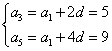
![]()
∴ ![]()
![]()
( = 2 \* ROMAN II) ![]()
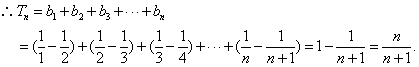
17解:( = 1 \* ROMAN I) ![]()
且 ![]()
∴ ![]()
![]()
![]()
( = 2 \* ROMAN II)由题意可知: ![]()
∴ ![]()
由余弦定理可得: ![]()
∴ ![]()
又 ![]()
![]()
18、解:由题意可知,用汽车运输的总支出为:
![]()
用火车运输的总支出为:
![]()
(1)由 ![]()
![]()
(2)由 ![]()
![]()
(3)由 ![]()
![]()
答:当A、B两地距离小于 ![]()
当A、B两地距离等于 ![]()
当A、B两地距离大于 ![]()
19、(14分)解:(1) ![]()
![]()
![]()
![]()
![]()
解得 ![]()
(2) ![]()
![]()
![]()
![]()
又 ![]()
![]()
而 ![]()
![]()
![]()
![]()
![]()
故 ![]()
![]()
20、解:(1) ![]()
![]()
![]()
![]()
![]()
![]()
设 ![]()
![]()
![]()
所以, ![]()
![]()
(2)由(1)可知 ![]()
由 ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
于是要使 ![]()
![]()
![]()
即 ![]()
![]()
![]()
设 ![]()

![]()
![]()
故存在实数 ![]()
21、解:(1)由 
![]()
![]()
![]()
![]()
![]()
又 ![]()
![]()
![]()
当 ![]()
![]()
![]()
当 ![]()
![]()
![]()
当 ![]()
![]()
![]()
(2)依题 ![]()
![]()
![]()

解得 ![]()
![]()
(3) ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
又 ![]()
![]()
![]()
![]()
![]()