| |
|
[组图]高考数学二轮复习综合试卷
|
| 查询数高三上末的详细结果
|
|
高考数学二轮复习综合试卷(一)
一、填空题:本大题共14小题,每小题5分,共70分.把答案填写在答题卡相应位置上.
1.设 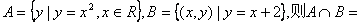 ▲
▲
2.复数 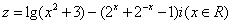 在复平面内对应的点位于第 ▲ 象限
在复平面内对应的点位于第 ▲ 象限
3.容量为100的样本数据,按从小到大的顺序为8组,如下表: |
组数 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 | |
频数 |
10 |
13 |
x |
14 |
15 |
13 |
12 |
9 | |
第3组的频率为 ▲
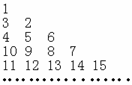 4.自然数列按如右图规律排列,若数 4.自然数列按如右图规律排列,若数 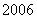 在第
在第 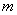 行第
行第 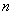 个数,
个数,
则 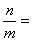 ▲
▲
5.把函数 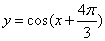 1的图象向左平移
1的图象向左平移 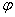 个单位,所得的图象对应的函数为偶函数,则
个单位,所得的图象对应的函数为偶函数,则 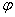 的最小正值为 ▲
的最小正值为 ▲
6.从编号为1、2、3、4、5、6的六名运动员中选四名运动员参加1500米中长跑比赛,其中3号运动员参加比赛的概率是 ▲
7.小聪预备购买一台价值6000元的电脑,但现款不够,商店答应分期付款,即在1年内分12次付款(购买时第一次付款,购买后每满1个月付款一次),每次付款数目相同,若月利率为0.8%,按复利计算,则每次应该付款 ▲
 8.椭圆 8.椭圆 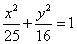 的左、右焦点分别为F1,F2 ,弦AB过F1 ,若△ABF2的内切圆周长为
的左、右焦点分别为F1,F2 ,弦AB过F1 ,若△ABF2的内切圆周长为 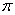 ,A,B两点的坐标分别为(x1,y1)和(x2,y2),则| y2-y1|的值为 ▲
,A,B两点的坐标分别为(x1,y1)和(x2,y2),则| y2-y1|的值为 ▲
9.如右图是函数 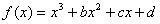 的大致图象,则
的大致图象,则
 等于 ▲
等于 ▲
10.用棱长为 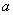 的正方体形纸箱放一棱长为
的正方体形纸箱放一棱长为  的正四面体形零件,使其能完全放入纸箱内,则此纸箱容积的最小值为 ▲
的正四面体形零件,使其能完全放入纸箱内,则此纸箱容积的最小值为 ▲
11.已知数列{  }的通项公式上
}的通项公式上  (
( 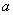 、
、 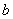 为常数),其前
为常数),其前 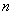 项和为
项和为 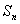 ,若平面上的三个不共线的向量
,若平面上的三个不共线的向量 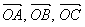 满足
满足 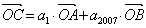 ,且A、B、C三点共线,则S2007= ▲
,且A、B、C三点共线,则S2007= ▲
|
S!0
I!1
While S<60

 S!S I
S!S I
I! I 1
End While
(12题图)
| | 12. 观察下列程序,该循环变量I共
循环了 ▲ 次
13.学号分别为1、2、3、4、5的五个学生在计算机机房操作编号分别为1、2、3、4、5的计算机。假如第 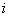 的学生操作第
的学生操作第 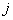 号的计算机,规定记作为
号的计算机,规定记作为 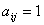 ,否则
,否则 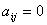 (一台计算机可以答应多个学生合作操作),现有等式
(一台计算机可以答应多个学生合作操作),现有等式 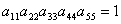 ,那么等式说明。
,那么等式说明。
▲ (用文字语言表述)
14.给出以下五个命题:① 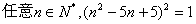 .
.
②已知x,y满足条件  y的最大值为8,则k=-6.
y的最大值为8,则k=-6.
③设全集U={1,2,3,4,5,6},集合 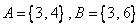 ,则
,则 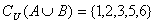 .
.
④定义在 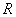 上的函数
上的函数 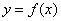 在区间
在区间 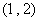 上存在唯一零点的充要条件是
上存在唯一零点的充要条件是 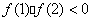 .
.
⑤已知 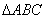 所在平面内一点
所在平面内一点 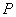 (
( 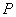 与
与 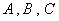 都不重合)满足
都不重合)满足 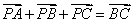 ,
,
则  与
与 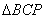 的面积之比为
的面积之比为 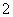 .
.
其中正确命题的序号是 ▲
二、解答题:本大题共6小题,共90分.请在答题卡指定区域内作答,解答时应写出文字说明、证实过程或演算步骤.
15.(本小题满分14分)已知 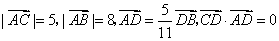 ,
,
(1)求 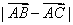 ;
;
(2)设 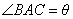 ,且已知
,且已知 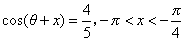 ,求
,求 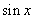 。
。
 16.(本小题满分14分)如图在正四棱柱ABCD-A1B1C1D1中,AB= 16.(本小题满分14分)如图在正四棱柱ABCD-A1B1C1D1中,AB= 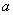 ,
,
AA1=2 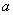 ,M、N分别是BB1、DD1的中点.
,M、N分别是BB1、DD1的中点.
(1)求证:平面A1MC1⊥平面B1NC1;
(2)若在正四棱柱ABCD-A1B1C1D1的体积为V,
三棱锥M-A1B1C1的体积为V1,求V1:V的值.
17.(本小题满分15分)已知圆 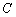 :
:  .
.
(1)直线 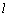 过点
过点 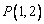 ,且与圆
,且与圆 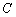 交于
交于 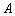 、
、 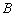 两点,若
两点,若 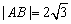 ,求直线
,求直线 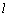 的方程;
的方程;
(2)过圆 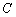 上一动点
上一动点 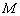 作平行于
作平行于 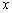 轴的直线
轴的直线 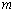 ,设
,设 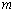 与
与 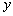 轴的交点为
轴的交点为 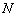 ,若向量
,若向量 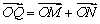 ,求动点
,求动点 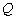 的轨迹方程,并说明此轨迹是什么曲线.
的轨迹方程,并说明此轨迹是什么曲线.
18.(本小题满分15分)我市现有从事第二产业人员100万人,平均每人每年创造产值 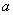 万元(
万元( 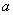 为正常数),现在决定从中分流
为正常数),现在决定从中分流  万人去加强第三产业。分流后,继续从事第二产业的人员平均每人每年创造产值可增加
万人去加强第三产业。分流后,继续从事第二产业的人员平均每人每年创造产值可增加 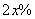 (
( 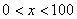 )。而分流出的从事第三产业的人员,平均每人每年可创造产值
)。而分流出的从事第三产业的人员,平均每人每年可创造产值 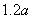 万元。
万元。
(1)若要保证第二产业的产值不减少,求  的取值范围;
的取值范围;
(2)在(1)的条件下,问应分流出多少人,才能使该市第二、三产业的总产值增加最多?
19.(本小题满分16分)已知函数 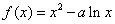 和
和 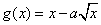 在
在 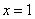 处的切线平行.⑴试求函数
处的切线平行.⑴试求函数  和
和 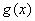 的单调增区间;
的单调增区间;
⑵设 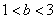 ,求证:
,求证:  .
.
20.(本小题满分16分)(Ⅰ)已知定义在 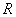 上的单调函数
上的单调函数  ,存在实数
,存在实数 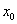 ,使得对于任意实数
,使得对于任意实数 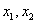 总有
总有 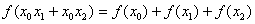 恒成立.
恒成立.
(1) 求 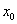 的值;
的值;
(2) 若 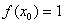 ,且任意正整数
,且任意正整数 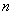 ,有
,有 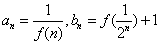 ,记
,记 
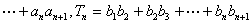 ,试比较
,试比较  与
与 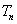 的大小关系,并给出证实.
的大小关系,并给出证实.
如东县中学2008届高三数学二轮复习综合试卷(一)参考答案
1. 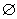 2.四 3.
2.四 3. 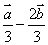 4.
4. 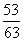 5.
5. 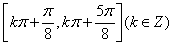 6.
6. 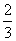 7.528 8.
7.528 8.  9.
9. 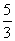 10.
10. 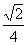 11.
11. 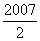 12.11 13.每个学生都在操作与之学号相同编号的计算机 14.②、⑤
12.11 13.每个学生都在操作与之学号相同编号的计算机 14.②、⑤
15.(1) 
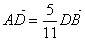 且
且 

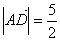

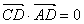

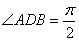
又 
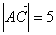

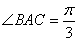
在 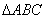 中,
中, 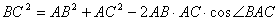

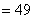

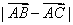 =7
=7
⑵由第一问得 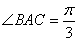

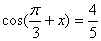

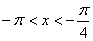

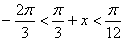
假设  ,则
,则 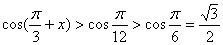
而 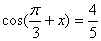
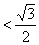
 假设不成立
假设不成立

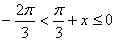

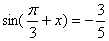

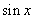
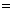
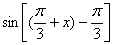
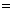

16.解:(1)取CC1的中点P,联结MP、NP、D1P
则A1MPD1为平行四边形 ∴ D1P∥A1M,∵A1B1C1D1是边长
为 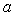 的正方形,又C1P=
的正方形,又C1P= 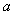 ,
,
∴C1PND1也是正方形,∴C1N⊥D1P.∴C1N⊥A1M.
又 C1B1⊥A1M,∴ A1M⊥平面B1NC1,又A1M  平面A1MC1,
平面A1MC1,
∴平面A1MC1⊥平面B1NC1;
(2)V= 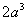 ,VM-A1B1C1=VC-MA1B1=
,VM-A1B1C1=VC-MA1B1= 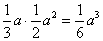 ,∴ V1:V =
,∴ V1:V = 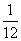
17.解(Ⅰ)①当直线 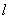 垂直于
垂直于  轴时,则此时直线方程为
轴时,则此时直线方程为 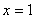 ,
, 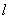 与圆的两个交点坐标为
与圆的两个交点坐标为 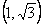 和
和 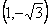 ,其距离为
,其距离为 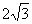 ,满足题意
,满足题意
②若直线 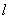 不垂直于
不垂直于  轴,设其方程为
轴,设其方程为 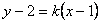 ,即
,即 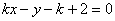
设圆心到此直线的距离为 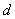 ,则
,则 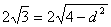 ,得
,得 
∴  ,
, 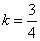 ,
,
故所求直线方程为 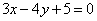
综上所述,所求直线为 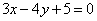 或
或 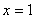
(Ⅱ)设点 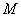 的坐标为
的坐标为 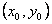 ,
,  点坐标为
点坐标为 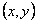
则  点坐标是
点坐标是 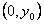
∵  ,
,
∴  即
即 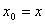 ,
, 
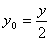
又∵ 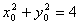 ,∴
,∴ 
由已知,直线m //ox轴,所以, 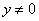 ,
,
∴  点的轨迹方程是
点的轨迹方程是 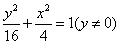 ,
,
轨迹是焦点坐标为 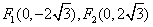 ,长轴为8的椭圆,并去掉
,长轴为8的椭圆,并去掉 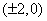 两点.
两点.
18.解:(1)由题意,得  。
。
(2)设该市第二、三产业的总产值增加 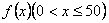 万元,则
万元,则
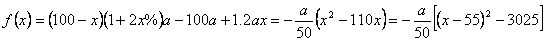 ∵
∵ 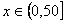 时,
时,  单调递增,∴
单调递增,∴ 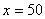 时,
时, 
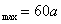 ,
,
即应分流出 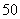 万人才能使该市第二、三产业的总产值增加最多。
万人才能使该市第二、三产业的总产值增加最多。
19.⑴∵  ,
, 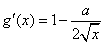 ,
,
由条件得  ,即
,即 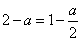 ,解得
,解得 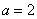 ,
,
令  ,解得
,解得 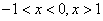 ,而
,而  ,
,
∴函数  的单调增区间为
的单调增区间为  ,
,
同理 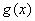 的单调增区间为
的单调增区间为  ;
;
⑵∵函数  在
在  上是增函数,且
上是增函数,且  ,
,
∴  ,
,
同理 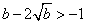 ,
,
∴ 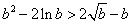 ,
,
∵ 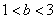 ,∴
,∴ 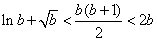 ,即
,即  .
.
20.解:(1)令 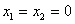 ,得
,得  . ①
. ①
令 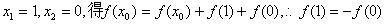 . ②
. ②
由①,②得: 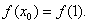
 为单调函数,
为单调函数, 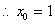
(2)由(1)得 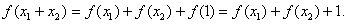
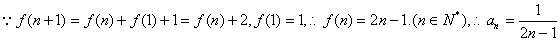 .
.
又 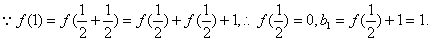
又 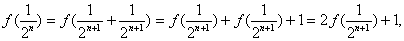
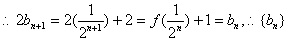 是等比数列,则
是等比数列,则 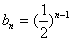 .
.
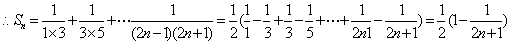
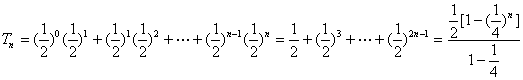 =
=
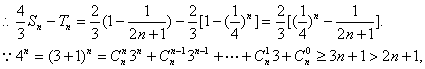
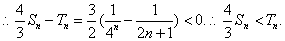
|
 8.椭圆
8.椭圆  16.(本小题满分14分)如图在正四棱柱ABCD-A1B
16.(本小题满分14分)如图在正四棱柱ABCD-A1B