| |
|
[组图]高考数学(文理科)模拟卷
|
| 查询数高三上末的详细结果
|
|
高考数学(文理科)模拟卷(一)
命题人:徐唐藩 校对:蒋李萍 方肇飞 编审:高三数学组
第(Ⅰ)卷 (选择题 共60分)
一.选择题(本大题12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项符合要求)
1.已知非空集合  、
、 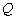 、
、 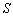 都是全集
都是全集  的子集,且
的子集,且 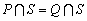 ,则( ).
,则( ).
A. 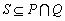 B.
B. 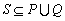 C.
C.  D.
D. 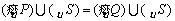
2.(文)在检查产品尺寸过程中,将其尺寸分成若干组, 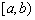 是其中一组,抽查出的个体在该组上频率
是其中一组,抽查出的个体在该组上频率
为 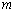 ,该组上的直方图的高为
,该组上的直方图的高为  ,则
,则  ( ).
( ).
A.  B.
B. 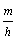 \* MERGEFORMAT
C.
\* MERGEFORMAT
C. 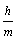 \* MERGEFORMAT
D.
\* MERGEFORMAT
D. 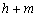
(理)在某学校举行的数学竞赛中,全体参赛学生的成绩近似服从正态分布 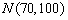 .已知成绩在
.已知成绩在
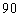 分以上(含
分以上(含 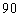 分)的学生有
分)的学生有 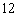 名,则此次竞赛的学生总人数约( )人.
名,则此次竞赛的学生总人数约( )人.
(参考数据: 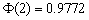 )
)
A.  B.
B. 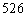 C.
C. 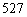 D.
D. 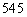
3.“ 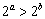 ”是 “
”是 “ 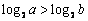 ”的( ).
”的( ).
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
4.等比数列中, 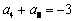 ,则
,则 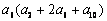 的值为( ).
的值为( ).
A. 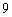 B.
B. 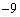 C.
C. 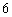 D.
D. 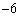
5.已知 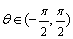 ,且
,且  ,其中
,其中  ,则关于
,则关于 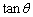 的值,以下四个答案中,可能正确
的值,以下四个答案中,可能正确
的是( ).
A. 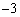 B.
B. 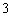 或
或 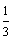 C.
C. 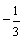 D.
D. 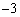 或
或 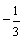
6.(文)若 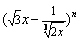 的展开式中含有常数项,则这样的正整数
的展开式中含有常数项,则这样的正整数  的最小值是( ).
的最小值是( ).
A. 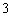 B.
B. 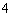 C.
C. 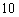 D.
D. 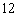
(理)函数 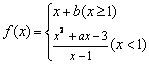 在
在 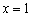 处连续,则
处连续,则 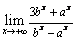 的值为( ).
的值为( ).
A. 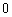 B.
B. 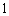 C.
C.  D.
D. 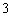
 7.下面四图都是同一坐标系中某三次函数及其导函数的图象,其中一定不正确的个数为( ). 7.下面四图都是同一坐标系中某三次函数及其导函数的图象,其中一定不正确的个数为( ).
A. 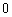 B.
B. 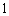 C.
C.  D.多于
D.多于  个
个
8.已知实数 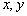 满足不等式组
满足不等式组  ,且
,且 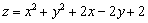 的最小值为
的最小值为  ,则实常数
,则实常数 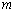 的
的
取值范围是( ).
A. 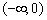 B.
B. 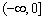 C.
C. 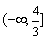 D.
D. 
9.在正方体  中,
中, 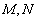 分别为
分别为 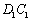 和
和 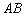 的中点,则
的中点,则 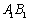 与平面
与平面  所成的角
所成的角
为( ).
A.  B.
B. 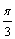 C.
C. 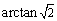 D.
D. 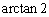
10.(文)设双曲线  的右准线与两条渐近线交于
的右准线与两条渐近线交于 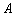 、
、 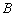 两点,右焦点为
两点,右焦点为 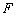 ,且
,且
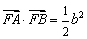 ,则双曲线的离心率为( ).
,则双曲线的离心率为( ).
A. 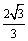 B.
B. 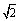 C.
C. 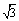 D.
D. 
(理)设双曲线 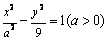 的左、右焦点为
的左、右焦点为 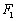 、
、 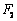 ,若该双曲线上有一点
,若该双曲线上有一点 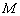 到点
到点 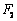 的距离为
的距离为
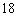 ,且
,且 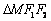 的内切圆圆心
的内切圆圆心 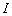 的横坐标为
的横坐标为 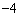 ,则该双曲线的离心率为( ).
,则该双曲线的离心率为( ).
A. 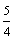 B.
B. 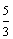 C.
C. 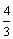 D.
D. 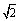
11.设  为
为 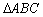 的内心,当
的内心,当 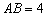 ,
, 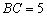 ,
, 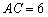 时,
时, 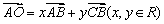 ,则
,则  ( ).
( ).
A. 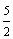 B.
B. 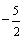 C.
C.  D.
D. 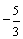
12.(文)已知二次函数 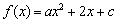 的值域是
的值域是 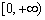 ,那么
,那么 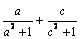 的最大值是( ).
的最大值是( ).
A. 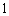 B.
B.  C.
C. 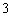 D.
D. 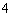
(理)已知二次函数 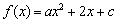 的值域是
的值域是 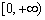 ,那么
,那么  的最小值是( ).
的最小值是( ).
A. 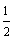 B.
B. 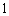 C.
C.  D.
D. 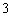
第(Ⅱ)卷 (非选择题 共90分)
二.填空题(本大题4个小题,每小题4分,共16分,把答案填在题中横线上)
13.已知函数  ,且
,且  ,则函数
,则函数  的值域为
的值域为  .
.
14.(文)已知抛物线 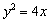 ,过点
,过点  的直线与抛物线交于两点
的直线与抛物线交于两点 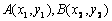 ,则
,则  的
的
最小值为  .
.
(理)已知抛物线 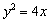 上的点
上的点  到抛物线的准线距离为
到抛物线的准线距离为  ,到直线
,到直线  的距离为
的距离为 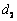 ,
,
则 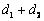 的最小值为
的最小值为  .
.
15.假如一个三位数 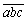 满足
满足 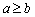 且
且 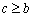 ,则称这样的三位数为“非凸数”(如
,则称这样的三位数为“非凸数”(如 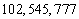 等),
等),
那么所有非凸数的个数是  .
.
 16.有两个相同的直三棱柱,高为 16.有两个相同的直三棱柱,高为  ,底面三角形的三边长
,底面三角形的三边长
分别为 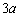 、
、 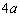 、
、  .用它们拼成一个三棱柱
.用它们拼成一个三棱柱
或四棱柱,在所有可能的情况中,全面积最小的是一个
四棱柱,则  的取值范围是
的取值范围是  .
.
三.解答题(本大题6个小题,共74分,解答题应写出文字说明、证实过程或演算步骤)
17.(本小题满分12分)
已知 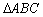 三内角
三内角 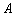 、
、 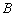 、
、 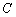 成等差数列,
成等差数列,  ,
,  .
.
(Ⅰ)若 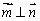 ,判定
,判定 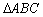 外形;
外形;
(Ⅱ)求 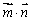 取得最大值时
取得最大值时 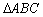 三内角的大小.
三内角的大小.
18.(本小题满分12分)(文)已知函数 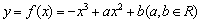 .
.
(Ⅰ)当 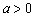 时,若
时,若  满足
满足 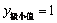 ,
, 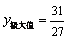 ,试求
,试求  的解析式;
的解析式;
(Ⅱ)当 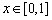 时,
时, 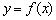 图象上的任意一点处的切线斜率
图象上的任意一点处的切线斜率 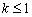 恒成立,求
恒成立,求  的取值范围.
的取值范围.
(理)已知函数 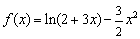 .
.
(Ⅰ)求  在
在  上的极值;
上的极值;
(Ⅱ)若对任意 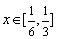 ,不等式
,不等式 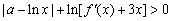 成立,求实数
成立,求实数  的取值范围.
的取值范围.
19.(本小题满分12分)(文)在中国红歌会的全国十强歌手中,有男歌手 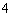 人,女歌手
人,女歌手 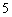 人,另一名为三
人,另一名为三
人组合歌手.现从中任选 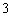 名歌手参加某专场演出.
名歌手参加某专场演出.
(Ⅰ)求三人组合歌手参加演出的概率;
(Ⅱ)求至多有  名男歌手参加演出的概率.
名男歌手参加演出的概率.
(理)盒中有 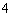 张卡片,其中
张卡片,其中 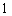 张写有字母
张写有字母 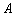 ,
, 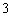 张写有字母
张写有字母 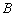 ,每次从中任取
,每次从中任取 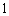 张卡片,直到取出卡
张卡片,直到取出卡
片 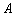 为止.
为止.
(Ⅰ)若不放回抽取卡片,求取卡片次数的期望和方差;
(Ⅱ)若有放回抽取卡片,求取卡片次数的分布列和期望值.
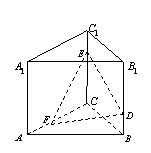 20.(本小题满分12分)如图,已知正三棱柱 20.(本小题满分12分)如图,已知正三棱柱 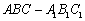 中,
中, 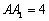 ,
,  ,点
,点  、
、 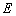 、
、 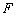 分别在
分别在
棱  、
、 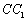 、
、 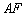 上,且
上,且 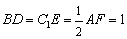 .
.
(Ⅰ)求平面  与平面
与平面  所成锐二面角的大小;
所成锐二面角的大小;
(Ⅱ)求点  到平面
到平面  的距离..
的距离..
21.(本小题满分12分)(文)已知数列 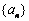 是首项
是首项  ,公比
,公比 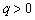 的等比数列.设
的等比数列.设
 ,且
,且 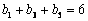 ,
, 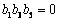 .
.
(Ⅰ)求数列 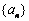 的通项公式;
的通项公式;
(Ⅱ)设  的前
的前  项和为
项和为 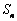 ,求当
,求当  最大时
最大时  的值.
的值.
(理)已知数列 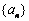 与
与  有如下关系:
有如下关系:  ,
, 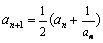 ,
, 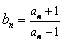 .
.
(Ⅰ)求数列  \* MERGEFORMAT
的通项公式;
\* MERGEFORMAT
的通项公式;
(Ⅱ)令  \* MERGEFORMAT
求数列
\* MERGEFORMAT
求数列 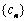 \* MERGEFORMAT
的通项公式;
\* MERGEFORMAT
的通项公式;
(Ⅲ)设 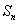 \* MERGEFORMAT
是数列
\* MERGEFORMAT
是数列 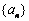 的前
的前  项和,当
项和,当  时,求证
时,求证 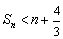 \* MERGEFORMAT
.
\* MERGEFORMAT
.
22.(本小题满分14分)(文)椭圆 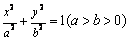 左、右焦点分别为
左、右焦点分别为 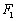 、
、 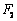 ,
,  是椭圆上一点,
是椭圆上一点,
 ,设
,设 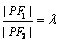 .
.
(Ⅰ)求椭圆离心率 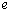 和
和 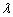 的关系式;
的关系式;
(Ⅱ)设 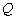 是离心率最小的椭圆上的动点,若
是离心率最小的椭圆上的动点,若 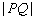 的最大值为
的最大值为  ,求椭圆的方程.
,求椭圆的方程.
(理)椭圆 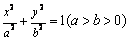 左、右焦点分别为
左、右焦点分别为 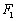 、
、 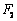 ,
,  是椭圆上一点,
是椭圆上一点,  ,
,
设 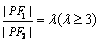 .
.
(Ⅰ)求椭圆离心率 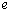 和
和 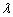 的关系式;
的关系式;
(Ⅱ)过  点离心率最小的椭圆的切线,交
点离心率最小的椭圆的切线,交  轴于
轴于 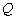 点,求证:
点,求证:  .
.
参考答案
命题人:徐唐藩 校对:涂彩琴 方肇飞 编审:高三数学组
一.选择题(本大题12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项符合要求) |
题号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 | |
答案 |
D |
文B
理B |
B |
A |
C |
文B 理D |
C |
B |
C |
文D 理A |
B |
文A 理B | |
提示:(文)
12.(文)由二次函数 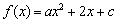 的值域是
的值域是 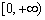 ,得
,得 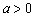 且
且 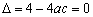 ,∴
,∴ 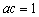 且
且
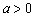 ,
, 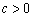 .∴
.∴  .当
.当 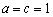 时取等号.
时取等号.
(理)提示:由二次函数 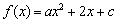 的值域是
的值域是 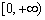 ,得
,得 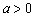 且
且 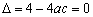 ,∴
,∴ 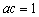 且
且
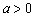 ,
, 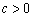 .∴
.∴ 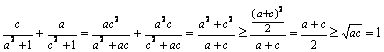 .
.
当 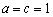 时取等号.
时取等号.
二.填空题(本大题4个小题,每小题4分,共16分,把答案填在题中横线上)
13.  14.(文)
14.(文) 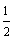 (理)
(理) 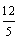 15.
15. 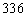 16.
16. 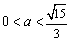
三.解答题(本大题6个小题,共74分,解答题应写出文字说明、证实过程或演算步骤)
17.(本小题满分12分)解:(Ⅰ)由 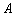 、
、 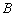 、
、 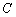 成等差数列及
成等差数列及  ,知
,知  .
.
∵ 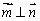 ,∴
,∴ 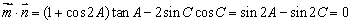 .由
.由 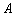 、
、 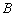 、
、 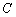 为三角形
为三角形
内角,且 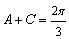 ,∴
,∴ 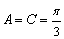 ,故
,故 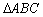 为等边三角形.
为等边三角形.
(Ⅱ)  ,
,
∴当  时,
时, 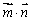 取得最大值
取得最大值 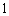 ,此时,
,此时,  ,
,  .
.
18.(本小题满分12分)(文) 解:(Ⅰ)由 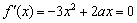 ,得
,得 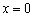 或
或 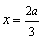 .
.
当 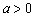 ,
,  变化时,
变化时, 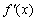 、
、  的变化如下表:
的变化如下表:
∴  ,
,  ,解得
,解得 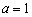 ,
, 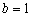 .∴
.∴ 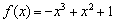 .
.
(Ⅱ)由题意, 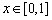 时,恒有
时,恒有 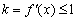 ,即
,即 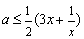 恒成立.∵
恒成立.∵  ,当且仅当
,当且仅当
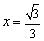 时取等号,∴
时取等号,∴  ,故
,故  的取值范围为
的取值范围为 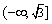 .
.
(理)解:(Ⅰ) 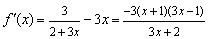 ,令
,令 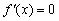 得
得  或
或 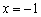 (舍去)
(舍去)
∴当 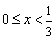 时,
时,  单调递增;当
单调递增;当 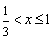 时,
时, 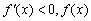 单调递减.
单调递减.
∴ 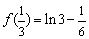 为函数
为函数  在
在  上的极大值.
上的极大值.
(Ⅱ)由 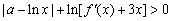 得,
得,  或
或  .
.
设 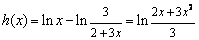 ,
, 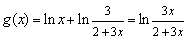 ,依题意知
,依题意知 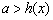 或
或
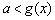 在
在 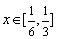 上恒成立, ∵
上恒成立, ∵  ,
,
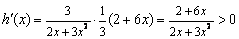 ,∴
,∴  与
与 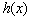 都在
都在  上单增,要使不等式①
上单增,要使不等式①
成立,当且仅当 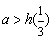 或
或 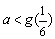 ,即
,即 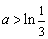 或
或 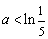 .
.
19.(本小题满分12分)(文)解:(Ⅰ) 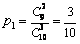 .
.
(Ⅱ) 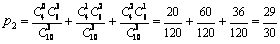 或
或 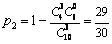 .
.
(理)解:(Ⅰ)取卡片次数 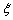 的可能值为
的可能值为  .∴
.∴  .
. 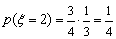 ,
,
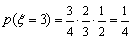 ,
,  .故
.故 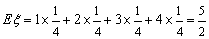 .
.
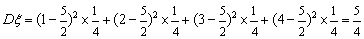 .
.
(Ⅱ)设有放回抽取卡片时,取卡片次数为 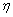 ,则
,则 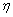 的可能值为
的可能值为  .
.
∵ 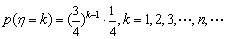 ,
,
∴ 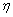 的分布列为:
的分布列为:
∴ 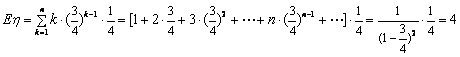 .
.
20.(本小题满分12分)解:(Ⅰ)延长  、
、 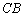 相交于点
相交于点 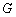 ,连结
,连结  ,则二面角
,则二面角 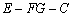
的大小为所求.作 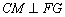 于点
于点 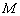 ,连结
,连结 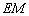 ,由三垂线定理知
,由三垂线定理知
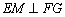 .∴
.∴ 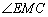 为所求二面角的大小.由已知
为所求二面角的大小.由已知  ,
, 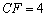 ,
,
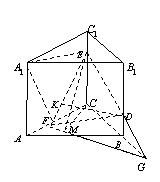  .由余弦定理得,
.由余弦定理得, 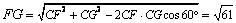 .
.
∴ 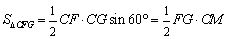 ,可得
,可得 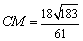 .
.
在  中,
中, 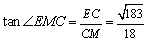 ,则所求角为
,则所求角为 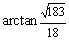 .
.
(Ⅱ)由已知矩形 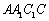 的面积为
的面积为 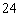 ,
,  ,
, 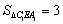 ,
,  ,
,
∴ 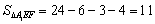 .取
.取 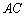 的中点
的中点  ,则
,则 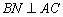 .
.
作 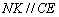 交
交  于点
于点 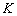 ,可得
,可得 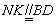 ,∴
,∴ 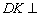 平面
平面  ,
, 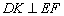 .由
.由  ,
,
 ,得
,得 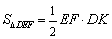
 .设所求距离为
.设所求距离为 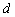 ,则由
,则由  得,
得,
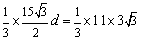 ,∴
,∴ 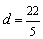 为所求.
为所求.
21.(本小题满分12分)
(文)解:(Ⅰ) 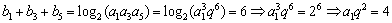 .∵
.∵  ,
,
∴  .又
.又 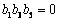 ,若
,若  ,则
,则 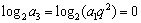 ,即
,即 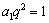 ,这与
,这与 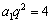
矛盾,故 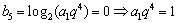 .∴
.∴ 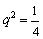 ,
, 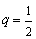 ,
, 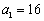 .∴
.∴  .
.
(Ⅱ)∵ 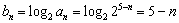 ,∴
,∴  是首项为
是首项为 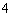 ,公差为
,公差为 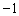 的等差数列,∴
的等差数列,∴ 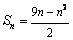 ,
,
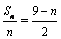 .故
.故 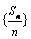 是首项为
是首项为 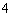 ,公差为
,公差为 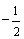 的等差数列.∵
的等差数列.∵ 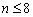 时,
时, 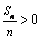 ;
; 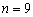 时,
时,  ;
;
 时,
时, 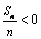 .故当
.故当 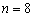 或
或 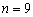 时,
时,  最大.
最大.
(理)解:(Ⅰ)∵  \* MERGEFORMAT
,∴
\* MERGEFORMAT
,∴  .
.
∴ 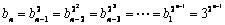 \* MERGEFORMAT
.
\* MERGEFORMAT
.
(Ⅱ)由(Ⅰ)知 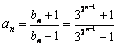 ,∴
,∴ 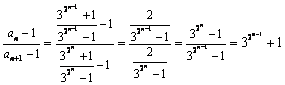 \* MERGEFORMAT
.
\* MERGEFORMAT
.
∴  .
.
(Ⅲ)∵当  时,
时, 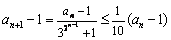 ,当且仅当
,当且仅当 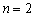 \* MERGEFORMAT
时取等号.且
\* MERGEFORMAT
时取等号.且 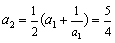 ,
,
故 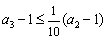 ,
, 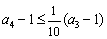 ,……,
,……, 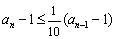 . 以上
. 以上 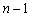 个式子相加,
个式子相加,
得 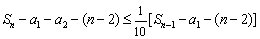 ,∴
,∴  ,
,
∴  ,∴
,∴ 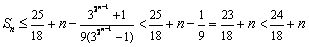 .
.
故 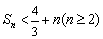 得证.
得证.
22.(本小题满分14分)(文)解:(Ⅰ) 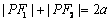 ,
, 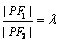 ,∴
,∴ 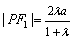 ,
, 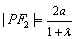 .
.
由余弦定理, 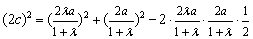 ,得
,得  .
.
(Ⅱ)由(Ⅰ)知 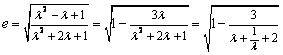 ,
, 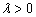 ,
, 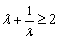 ,∴
,∴ 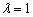 时,
时,
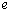 的最小值为
的最小值为 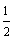 .当
.当 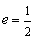 时,
时, 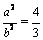 .可设椭圆的方程
.可设椭圆的方程 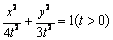 此时由
此时由 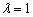 得,
得,
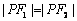 ,∴
,∴ 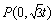 .设
.设  ,则
,则 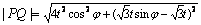
 .当
.当 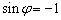 时,
时, 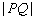 的最大值为
的最大值为 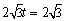 ,
,
∴ 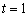 ,故椭圆的方程
,故椭圆的方程 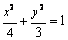 .
.
(理)解:(Ⅰ) 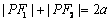 ,
, 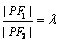 ,∴
,∴ 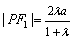 ,
, 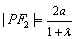 .由余弦定理,
.由余弦定理,
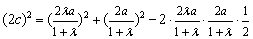 ,得
,得  .
.
(Ⅱ)由(Ⅰ)知 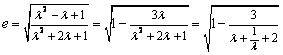 .设
.设 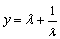 ,知
,知 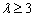 时,
时, 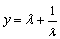 在
在
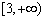 上单调递增,∴
上单调递增,∴ 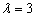 时,
时, 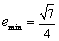 ,得
,得 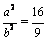 .设
.设 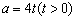 ,则
,则 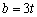 ,
, 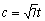 .不妨设
.不妨设
点  在第一象限.由
在第一象限.由  ,
, 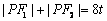 得,
得,  ,∴
,∴ 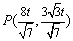 .
.
设  是椭圆上动点,则
是椭圆上动点,则 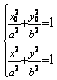 ,相减得
,相减得 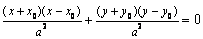 ,
,
即  .则
.则 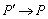 时,
时, 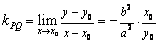 .设切线
.设切线 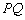 的方程为:
的方程为:
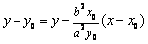 ①, 又
①, 又  ②. 将②代入①整理得,
②. 将②代入①整理得, 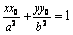 .
.
令 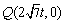 得,
得, 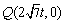 ,∴
,∴  .又
.又  ,故
,故  .
.
|
