|
高考数学文科第一次联考
数学文科
本试卷分第I卷(选择题)和第II卷(非选择题)两部分。满分150分。考试用时120分钟。
第I卷(选择题 共60分)
一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的.
1.若 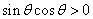 ,则
,则 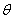 在( )
在( )
A.第一象限 B.第一、二象限 C.第一、三象限 D.第二、四象限
2. “ 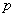 或
或 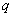 是假命题”是“非
是假命题”是“非 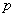 为真命题”的 ( )
为真命题”的 ( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
3.已知全集U=R,设函数 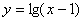 的定义域为集合A,函数
的定义域为集合A,函数 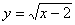 的定义域为集合B,则
的定义域为集合B,则 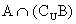 = ( )
= ( )
A.[1,2] B.[1,2 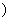 C.
C. 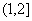 D.(1,2)
D.(1,2)
4.若点 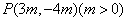 在角
在角 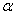 的终边上,则
的终边上,则 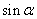 的值是( )
的值是( )
A、 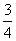 B、
B、 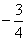 C、
C、 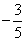 D、
D、 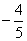
5.设集合A和集合B都是实数集R,映射f: 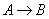 把集合A中的元素x映射到集合B中元素x3-x+2,则在映射f下,象2的原象所成的集合是( ) 把集合A中的元素x映射到集合B中元素x3-x+2,则在映射f下,象2的原象所成的集合是( )
A .{1} B.{0,1,-1} C.{0 } D.{0,-1,-2}
6. 等差数列{an}的前n项和为Sn,若a3 a7 a11=6,则S13=( )
A.24 B.25 C.26 D.27
7.要得到函数 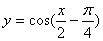 的图象,只需将
的图象,只需将 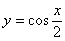 的图象( )
的图象( )
A.向左平移 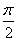 B.向右平移
B.向右平移 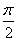 C.向左平移
C.向左平移 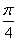 D.向右平移
D.向右平移 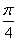
8.已知向量 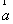 、
、 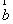 满足|
满足| 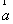 |=1,|
|=1,| 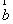 |=4,且
|=4,且 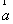 ·
· 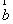 =2,则
=2,则 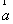 与
与 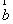 的夹角为 ( )
的夹角为 ( )
(A) 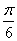 (B)
(B) 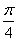 (C)
(C)  (D)
(D) 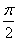
9.下列命题中:(1)向量  与
与 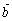 是两个单位向量,则
是两个单位向量,则  与
与 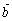 相等;(2)在
相等;(2)在 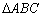 中,必有
中,必有  ;(3)若
;(3)若  ,
, 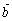 均为非零向量,则
均为非零向量,则 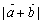 与
与 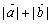 一定相等;(4)向量
一定相等;(4)向量 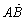 与
与  是共线向量,则点A、B、C、D必在同一条直线上;(5)若向量
是共线向量,则点A、B、C、D必在同一条直线上;(5)若向量  与
与 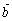 同向,且
同向,且 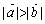 ,则
,则 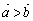 .其中假命题的个数为( )
.其中假命题的个数为( )
A.2 B. 3 C.4 D.5
10.函数y=2sin(2x 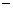 \* MERGEFORMAT
\* MERGEFORMAT
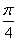 \* MERGEFORMAT
)的一个单调递减区间是( )
\* MERGEFORMAT
)的一个单调递减区间是( )
A、 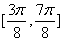 \* MERGEFORMAT
B、
\* MERGEFORMAT
B、 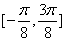 \* MERGEFORMAT
C、
\* MERGEFORMAT
C、 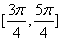 \* MERGEFORMAT
D、
\* MERGEFORMAT
D、 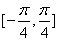 \* MERGEFORMAT
\* MERGEFORMAT
11.设 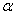 、
、 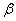 为钝角且
为钝角且 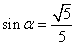 ,
, 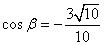 ,则
,则 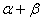 的值为( )
的值为( )
A、 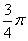 B、
B、 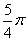 C、
C、 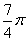 D、
D、 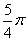 或
或 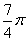
12.已知 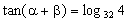 ,
, 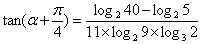 ,则
,则  ( )
( )
A. 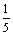 B.
B. 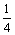 C.
C. 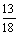 D.
D. 
第II卷(非选择题 共90分)
13.已知函数 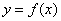 的反函数为
的反函数为 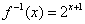 ,则
,则 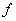 (1)=
(1)=
14.在直角坐标系中,始边为x轴的正半轴, 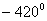 的终边与单位圆所构成的扇形的劣弧长等于 。
的终边与单位圆所构成的扇形的劣弧长等于 。
15.在数列{an}中,已知 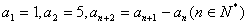 ,则a2007等于 ____
,则a2007等于 ____
16.给出下列命题:
①存在实数 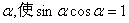 ;②存在实数
;②存在实数 
③ 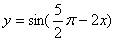 是偶函数;④
是偶函数;④ 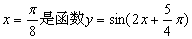 的一条对称轴方程;
的一条对称轴方程;
⑤若 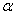 、
、 
其中正确命题的序号是 .(注:把所有正确命题的序号都填上)
17.(本小题满分12分)
已知 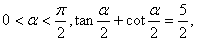 \* MERGEFORMAT
\* MERGEFORMAT
求(1)sinα,cosα的值;
(2)求 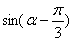 \* MERGEFORMAT
的值
\* MERGEFORMAT
的值
18.(本小题满分12分)
已知平面向量a 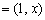 ,b
,b 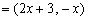
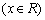 .
.
(Ⅰ)若a⊥b ,求x的值;
(Ⅱ)若a∥b ,求|a-b|.
19(本小题共12分)
已知函数 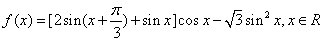
(Ⅰ)求函数 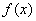 的最小正周期;
的最小正周期;
(Ⅱ)若 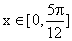 ,求函数
,求函数 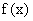 的最大值和最小值.
的最大值和最小值.
20.已知函数 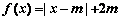 .
.
(Ⅰ)若函数 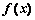 为偶函数,求
为偶函数,求 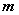 的值;
的值;
(Ⅱ)若 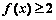 对一切
对一切 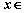 R恒成立,试求
R恒成立,试求 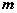 的取值范围.
的取值范围.
21.已知 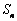 是数列
是数列 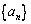 的前
的前 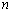 项和,
项和, 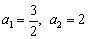 ,且
,且 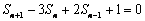 ,其中
,其中 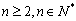 .
.
22.(本小题满分12分)
已知函数 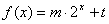 的图象经过点A(1,1)、B(2,3)及C(
的图象经过点A(1,1)、B(2,3)及C( 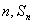 ),Sn为数列{
),Sn为数列{ 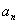 }的前n项和,
}的前n项和,  .
.
(1)求Sn及an;
(2)若数列 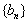 满足
满足 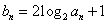 ,记
,记 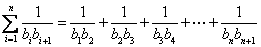
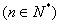 , 求证:
, 求证: 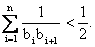
参考答案
1.C 2.A 3.D 4.D 5.B 6.C 7.B 8.C 9.B 10.A 11.C 12.B
13. 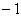 14.
14. 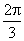 15.4 16. ③④
15.4 16. ③④
17.(1) 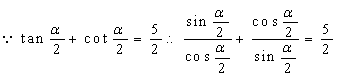 \* MERGEFORMAT
\* MERGEFORMAT
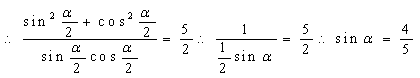 \* MERGEFORMAT
………6分
\* MERGEFORMAT
………6分
又 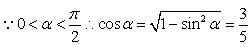 \* MERGEFORMAT
………8分
\* MERGEFORMAT
………8分
(2) 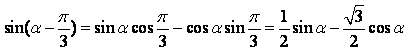 \* MERGEFORMAT
……11分
\* MERGEFORMAT
……11分
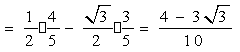 \* MERGEFORMAT
………13分
\* MERGEFORMAT
………13分
18.解:(Ⅰ)若a⊥b ,则a·b 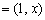 ·
· 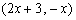
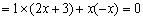 .
.
整理得 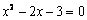 ,解得:
,解得: 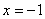 或
或 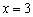 .………………………4分
.………………………4分
(Ⅱ)若a∥b ,则有 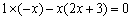 ,即
,即 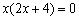 .
.
解得: 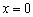 或
或 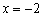 .………………………………………………8分
.………………………………………………8分
当 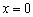 时,a
时,a  ,b
,b  ;
;
∴|a-b|=| 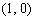
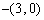 |=|
|=|  |
| 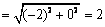 .………………10分
.………………10分
当 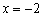 时,a
时,a 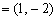 ,b
,b 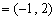 ;
;
∴|a-b|=| 
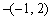 |=|
|=| 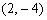 |
|  . ……13分
. ……13分
19解: 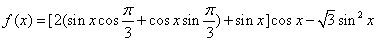
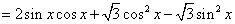
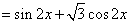
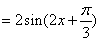 ………………………………6分
………………………………6分
(Ⅰ)函数 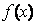 的最小正周期
的最小正周期 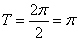 …………………8分
…………………8分
(Ⅱ)当 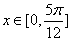 时,
时, 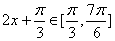 ………………9分
………………9分
当 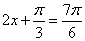 ,即
,即 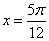 时,
时, 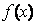 取最小值
取最小值 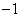 .………11分
.………11分
当 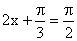 ,即
,即 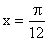 时,
时, 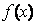 取最大值2…………………13分
取最大值2…………………13分
20.解.(Ⅰ) ∵ 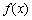 为偶函数,∴对于
为偶函数,∴对于 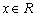 ,有
,有 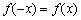 ,..............3分
,..............3分
∴  ,∴
,∴ 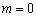 ...............6分
...............6分
(Ⅱ) ∵ 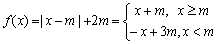 ,..............8分
,..............8分
∴ 函数 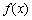 在
在 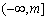 上递减,在
上递减,在 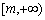 上递增,..............10分
上递增,..............10分
∴ 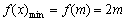 ,..............11分
,..............11分
要 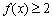 对一切
对一切 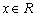 恒成立,只要
恒成立,只要 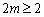 ,即
,即 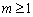 ...............13分
...............13分
21. 解:① 
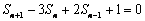



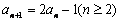 ........................................3分
........................................3分
又 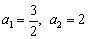 也满足上式,
也满足上式, 
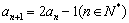

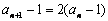 (
(  )
)
 数列
数列 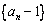 是公比为2,首项为
是公比为2,首项为 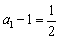 的等比数列.......................6分
的等比数列.......................6分
②由①, 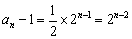
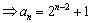 ................................8分
................................8分
于是 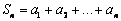
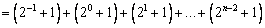
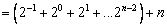
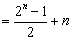 .................................................12分
.................................................12分
22.(1)由 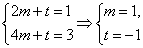 ∴
∴ 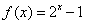
∴ 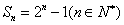 …………3分
…………3分
∴当 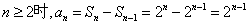 ,
, 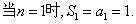
∴ 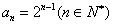 . …………6分
. …………6分
(2) 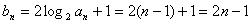 …………7分
…………7分
则 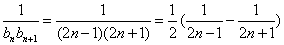 …………8分
…………8分
∴ 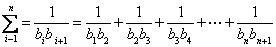
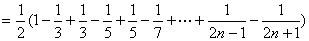
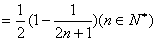 ……11分
……11分
综上可得:  …………12分
…………12分
|