|
高中毕业生文科数学二月调研测试试题
参考公式:
假如事件 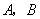 \* MERGEFORMAT
互斥,那么
\* MERGEFORMAT
互斥,那么 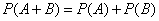 \* MERGEFORMAT
\* MERGEFORMAT
假如事件 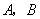 \* MERGEFORMAT
相互独立,那么
\* MERGEFORMAT
相互独立,那么 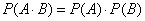 \* MERGEFORMAT
\* MERGEFORMAT
假如事件 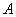 \* MERGEFORMAT
在一次试验中发生的概率是
\* MERGEFORMAT
在一次试验中发生的概率是 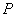 \* MERGEFORMAT
,那么
\* MERGEFORMAT
,那么  \* MERGEFORMAT
次独立重复试验中恰好发生
\* MERGEFORMAT
次独立重复试验中恰好发生 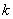 \* MERGEFORMAT
次的概率
\* MERGEFORMAT
次的概率 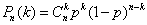 \* MERGEFORMAT
\* MERGEFORMAT
球的表面积公式 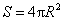 其中R表示球的半径
其中R表示球的半径
球的体积公式 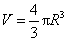 \* MERGEFORMAT
其中R表示球的半径
\* MERGEFORMAT
其中R表示球的半径
一.选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的
1、 数 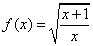 \* MERGEFORMAT
的定义域是
\* MERGEFORMAT
的定义域是
A、 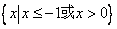 B、
B、 
C、 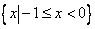 D、
D、 
2、在等差数列 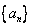 中,
中, 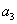 =9,
=9, 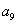 =3,则
=3,则 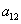 =
=
A、-3 B、0 C、3 D、6
3、已知实数 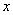 、
、 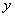 满足
满足 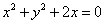 ,则
,则 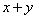 的最小值为
的最小值为
A、 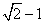 B、
B、 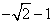 C、
C、 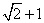 D、
D、 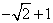
4、下面给出四个命题:
①直线 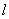 与平面
与平面 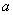 内两直线都垂直,则
内两直线都垂直,则  。②经过直线
。②经过直线 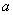 有且仅有一个平面垂直于直线
有且仅有一个平面垂直于直线 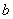 ③过平面
③过平面 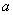 外两点,有且只有一个平面与
外两点,有且只有一个平面与 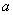 垂直。④直线
垂直。④直线 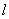 同时垂直于平面
同时垂直于平面 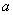 、
、  ,则
,则 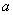 ∥
∥  。其中正确的命题个数为
。其中正确的命题个数为
A、3 B、2 C、1 D、0
5、二项式 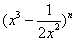 的展开式中含有非零常数项,则正整数n的最小值为
的展开式中含有非零常数项,则正整数n的最小值为
A、10 B、3 C、7 D、5
6、函数 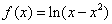 的单调递增区间为
的单调递增区间为
A、  B、(-0,1) C、
B、(-0,1) C、  D、
D、 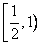
7、将长为15的木棒截成长为整数的三段,使它们构成一个三角形的三边,则得到的不同三角形的个数为
A、8 B、7 C、6 D、5
8.在(0, 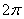 )内,使
)内,使 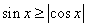 成立的
成立的 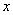 的取值范围为
的取值范围为
A、[ 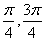 ] B、[
] B、[ 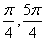 ] C、[
] C、[ 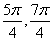 ] D、[
] D、[ 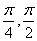 ]
]
9.设平面内有△ABC及点O,若满足关系式:  ,那么△ABC一定是
,那么△ABC一定是
A、直角三角形 B、等腰直角三角形 C、等腰三角形 D、等边三角形
10.在正四棱锥S-ABCD中,侧面与底面所成角为 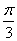 ,则它的外接球的半径R与内径球半径r的比值为
,则它的外接球的半径R与内径球半径r的比值为
A、5 B、 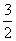 C、10 D、
C、10 D、 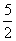
二.填空题:本大题共5小题,每小题5分,共25分,把答案填在题在横线上。
11、  ,则
,则  。
。
12、函数 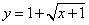 的反函数为 。
的反函数为 。
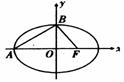 13、如图,已知A、B两点分别是椭圆C: 13、如图,已知A、B两点分别是椭圆C: 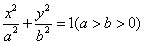 的左顶点和上顶点,而F是椭圆C的右焦点,若
的左顶点和上顶点,而F是椭圆C的右焦点,若 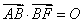 ,则椭圆C的离心率e= .
,则椭圆C的离心率e= .
14、假如变量 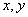 满足
满足 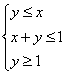 ,则
,则 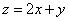 的最大值为 。
的最大值为 。
15.已知圆C: 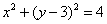 ,一动直线l过A (-1,O)与圆C相交于P、Q两点,M是PQ中点,l与直线
,一动直线l过A (-1,O)与圆C相交于P、Q两点,M是PQ中点,l与直线 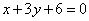 相交于N,则
相交于N,则 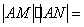 。
。
三.解答题:本大题共6小题,共75分,解答应写出文字说明、证实过程或演算步骤。
16.(本小题满分12分)
已知函数 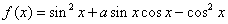 ,且
,且 
(1)求常数a的值及 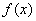 的最小值;
的最小值;
(2)当 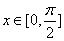 时,求
时,求 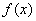 的单调增区间。
的单调增区间。
17.(本小题满分12分)
如图,在棱长为l的正方体ABCD-A1B1C1D1中,M为CC1中点。
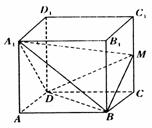 (1)求二面角A1-BD-M的大小; (1)求二面角A1-BD-M的大小;
(2)求四面体A1-BDM的体积;
18.(本小题满分12分)
一袋中放着写有1号至5号的5张纸牌,A、B两人按A、B、A、B,…的次序轮流从袋中不放回的取出1张纸牌,规定先取到5号纸牌者获胜。
(1)求B第一欠取牌就获胜的概率;
(2)求B获胜的概率。
19.(本小题满分12分)
设数列 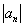 的前n项和
的前n项和  ,
, 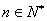 。
。
(1)求数列 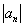 的通项公式
的通项公式 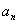 ;
;
(2)记  ,求数列
,求数列 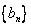 前n项和
前n项和 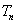
20.(本小题满分13分)
过双曲线C: 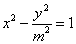 的右顶点A作两条斜率分别为k1、k2的直线AM、AN交双曲线C于M、N两点,其k1、k2满足关系式k1·k2=-m2且k1 k2
的右顶点A作两条斜率分别为k1、k2的直线AM、AN交双曲线C于M、N两点,其k1、k2满足关系式k1·k2=-m2且k1 k2 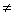 0,k1
0,k1 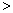 k2
k2
(1) 求直线MN的斜率;
(2) 当m2= 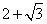 时,若
时,若 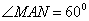 ,求直线MA、NA的方程;
,求直线MA、NA的方程;
21.(本小题满分14分)
函数 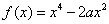 ,
, 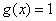 。
。
(1)求证:函数 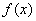 与
与 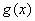 的图象恒有公共点;
的图象恒有公共点;
(2)当 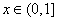 时,若函数
时,若函数 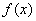 图象上任一点处切线斜率均小于1,求实数
图象上任一点处切线斜率均小于1,求实数 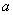 的取值范围;
的取值范围;
(3)当 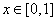 时,关于
时,关于 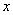 的不等式
的不等式 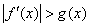 的解集为空集,求所有满足条件的实数
的解集为空集,求所有满足条件的实数 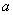 的值。
的值。
参考答案及评分细则
一.选择题 |
题号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 | |
答案 |
A |
B |
B |
C |
D |
C |
C |
A |
C |
D | |