|
高三文科数学第一学期期末教学质量检测
数学试题(文科)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分。考试时间120分钟。
第Ⅰ卷(选择题 共60分)
注重事项:
1.答第Ⅰ卷前,考生务必将自己的姓名、考号、学校、考试科目用铅笔涂写在答题卡上。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂连云港,如需改动,用橡皮擦干净后,再选涂其它答案,不能答在试卷上。
3.考试结束后,监考人员将本试卷和答题卡一并交回。
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知集合M是函数 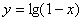 的定义域,集合
的定义域,集合 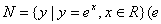 为自然对数的底数),则
为自然对数的底数),则 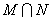 = ( )
= ( )
A. 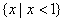 B.
B. 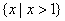 C.
C. 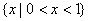 D.
D. 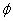
2. 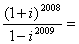 ( )
( )
A.22009i B.21004 C.21003(1 i) D.22008(1-i)
3.已知函数 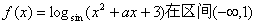 上递增,则实数a的取值范围是( )
上递增,则实数a的取值范围是( )
A.  B.[-4,-2] C.(-4,
B.[-4,-2] C.(-4,  ) D.(-
) D.(-  ,-2)
,-2)
4.设 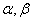 为两个不重合的平面,l,m,n为两两不重合的直线,给出下列四个命题:
为两个不重合的平面,l,m,n为两两不重合的直线,给出下列四个命题:
①若  ②若
②若 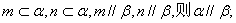
③若  ④
④ 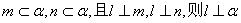 其中真命题的序号是 ( )
其中真命题的序号是 ( )
A.①③④ B.①②③ C.①③ D.②④
5.一个几何体的三视图如图所示,其中正视图中△ABC的边长为2的正三角形,俯视图为
正六边形,那么该几何体的侧视图的面积为 ( )
A. 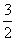 B.
B. 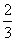 C.12 D.6
C.12 D.6
6.若方程  属于以下区间 ( )
属于以下区间 ( )
A. 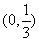 B.
B. 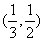 C.
C. 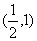 D.(1,2)
D.(1,2)
7.已知函数 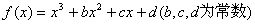 ,当
,当 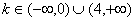 时,
时,  只有一个实数根;当
只有一个实数根;当 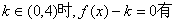 3个相异实根,现给出下列4个命题:
3个相异实根,现给出下列4个命题:
①函数  有2个极值点; ②函数
有2个极值点; ②函数  有3个极值点;
有3个极值点;
③  =4,
=4,  =0有一个相同的实根 ④
=0有一个相同的实根 ④  =0和
=0和  =0有一个相同的实根
=0有一个相同的实根
其中正确命题的个数是 ( )
A.1 B.2 C.3 D.4
8.将函数 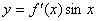 的图象向左平移
的图象向左平移  个单位,得到函数
个单位,得到函数 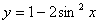 的图象,则
的图象,则  是 ( )
是 ( )
A. 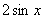 B.cosx C.sinx D.2cosx
B.cosx C.sinx D.2cosx
9.设 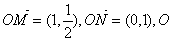 为坐标原点,动点
为坐标原点,动点 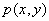 满足
满足
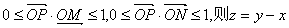 的最小值是 ( )
的最小值是 ( )
A.-1 B. 1 C.-2 D.1.5
10.如图,它们都表示的是输入所有立方小于1000的正整数的和的程序框图,那么判定框内应分别补充的条件是 ( )
A. 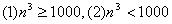
B. 
C. 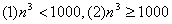
D. 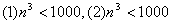
11.甲、乙两人各写一张贺年卡随意送给丙、
丁两人中的一人,则甲、乙将贺年卡送
给同一人的概率是 ( )
A.  B.
B. 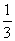
C. 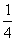 D.
D. 
12.已知点P(-3,1)在直线  ,过点P且方向向量为a=(2,-5)的入射光线,经y=-2反射后过椭圆的左焦点,则椭圆的离心率为 ( )
,过点P且方向向量为a=(2,-5)的入射光线,经y=-2反射后过椭圆的左焦点,则椭圆的离心率为 ( )
A.  B.
B. 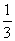 C.
C. 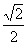 D.
D. 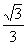
第Ⅱ卷(非选择题)
二、填空题
13.为了解学生答卷情况,寿光市教育部门在高三某
次测试后抽取了n名同学的第Ⅱ卷进行调查,并
根据所得数据画出了样本的频率分布直方图如图,
已知从左到右第一小组的频数是50,则
n= 。
14.设命题  对任意
对任意 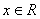 ,都有
,都有  成立,命题P且Q为假,P或Q为真,则实数a的取值范围是 。
成立,命题P且Q为假,P或Q为真,则实数a的取值范围是 。
15.已知a、b都是正实数,且满足 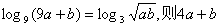 的最小值为 。
的最小值为 。
16.设函数  上的奇函数,且满足
上的奇函数,且满足  都成立,又当
都成立,又当 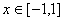 时,
时, 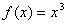 ,则下列四个命题:
,则下列四个命题:
①函数 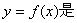 以4为周期的周期函数; ②当
以4为周期的周期函数; ②当 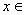 [1,3]时,
[1,3]时, 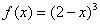 ;
;
③函数 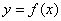 的图象关于x=1对称; ④函数
的图象关于x=1对称; ④函数 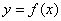 的图象关于点(2,0)对称,
的图象关于点(2,0)对称,
其中正确的命题序号是 。
三、解答题
17.(本小题满分12分)若向量 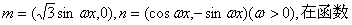
 的图象中,对称中心到对称轴的最小距离为
的图象中,对称中心到对称轴的最小距离为 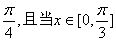 时,
时,  的最大值为1。
的最大值为1。
(1)求函数  的解析式;
的解析式;
(2)求函数  的单调递增区间。
的单调递增区间。
18.(本小题满分12分)数列 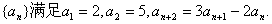
(1)求证:数列 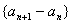 是等比数列;
是等比数列;
(2)求数列{ 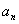 }的通项公式;
}的通项公式;
(3) 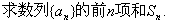
19.(本题满分2分)为了支持其贫困山区学校的教学工作,某市决定从5位优秀教师(二位女教师,三位男教师)中选派3位教师去该山区学校担任支教教师。设选派的3名老师中恰有2位女教师的概率为P(A);选派3名教师中至少有一位女教师的概率为P(B)。
(1)求P(A);
(2)求P(B);
(3)设函数 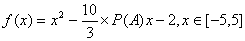 ,记“在函数定义域内任取一点x0,则
,记“在函数定义域内任取一点x0,则 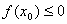 ”为事件C,求事件C的概率。
”为事件C,求事件C的概率。
20.(本小题满分12分)如图是一个几何体的三视图,请认真读图。
(1)有人说该几何体的侧棱PA垂直于底面ABCD,有人说四边形ABCD为矩形,也有人说PA不垂直于底面,请根据你的判定画出几何体的直观图;
(2)设AB的中点为M,PC中点为N,求证:MN//平面PAD;
(3)当AB=BC时,求证:平面PAC⊥平面BND。
21.(本小题满分12分)已知,椭圆 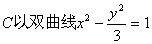 的焦点为顶点,以双曲线的顶点为焦点。
的焦点为顶点,以双曲线的顶点为焦点。
(1)求椭圆C的方程;
(2)若直线 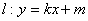 与椭圆C相交于M、N两点(M、N不是左右顶点),且以线段MN为直径的圆过点A,求证:直线l过定点,并求出该定点的坐标。
与椭圆C相交于M、N两点(M、N不是左右顶点),且以线段MN为直径的圆过点A,求证:直线l过定点,并求出该定点的坐标。
22.(本小题满分12分)设 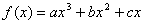 的极小值为-8,其导函数
的极小值为-8,其导函数 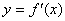 的图象经过点
的图象经过点 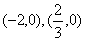 ,如图所示。
,如图所示。
(1)求  的解析式;
的解析式;
(2)若对 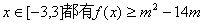 恒成立,求实数m的取值范围。
恒成立,求实数m的取值范围。
参考答案
一、选择题
1—12 C C A C A B C A A C A D
二、填空题
13.500 14.  15.25 16.①②③④
15.25 16.①②③④
三、解答题
17.解:由题意得 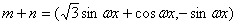

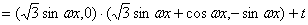
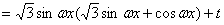

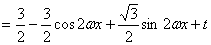
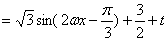 (4分)
(4分)
(1)∵对称中心到对称轴的最小距离为 
∴  的最小正周期T=
的最小正周期T= 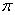
∴ 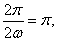
∴ 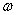 =1(6分)
=1(6分)
∴ 
当 

∴ 
∵ 
∴3 t=1
∴t=-2
∴  (8分)
(8分)
(2) 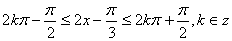 (10分)
(10分)
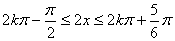
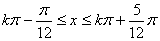
∴函数  的单调递增区间为
的单调递增区间为 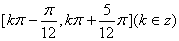 (12分)
(12分)
18.解(1)由题意知: 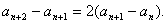
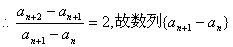 是等比数列(2分)
是等比数列(2分)
(2)由(1)知数列 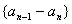 以是a2-a1=3为首项,
以是a2-a1=3为首项,
以2为公比的等比数列,所以 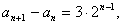
故a2-a1=3·20,所以a3-a2=3·21,a4-a3=3·22,…, 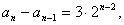
所以 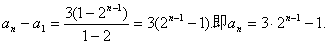 (8分)
(8分)
(3) 
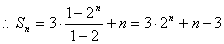 (12分)
(12分)
19.略
20.略
21.解:(1)椭圆方程为  (4分)
(4分)
(2)设M 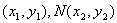 ,将
,将 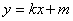 代入椭圆方程得
代入椭圆方程得
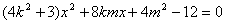
∴ 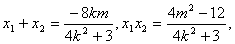 (6分)
(6分)
∵ 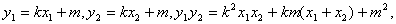
又以MN为直径的圆过点A(2,0),
∴ 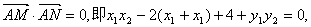
∴ 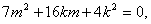
∴ 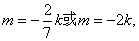 且满足
且满足 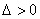 ,(9分)
,(9分)
若  ,直线l恒过定点(2,0)不合题意舍去,
,直线l恒过定点(2,0)不合题意舍去,
若 
22.解:(1) 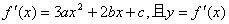 的图象过点
的图象过点 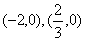
∴ 
∴ 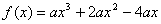 (2分)
(2分)
由图象知, 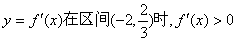 恒成立,
恒成立,
∴  上单调递增,
上单调递增,
同理可知,  上单调递减,
上单调递减,
∴  时,取得极小值,即
时,取得极小值,即 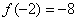 (4分)
(4分)

解得a=-1,
∴ 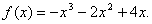 (6分)
(6分)
(2)要使对  都有
都有 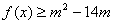 恒成立,
恒成立,
只需  即可(8分)
即可(8分)
由(1)可知,函数 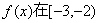 上单调递减,
上单调递减,
在 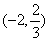 上单调递增,在
上单调递增,在  上单调递减,
上单调递减,
且 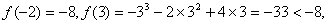
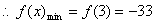 (10分)
(10分)
则-33 
故所求实数m的取值范围为[3,11](12分)
|