|
高考数学理科第一次联考
本试卷分第I卷(选择题)和第II卷(非选择题)两部分。满分150分。考试用时120分钟。
第I卷(选择题 共50分)
一、选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合题目要求的.
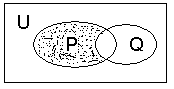 1.右图中阴影部分表示的集合是( ) 1.右图中阴影部分表示的集合是( )
A. 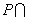
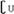 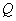 B.
B. 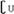 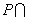
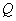
C. 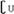 ( ( 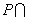
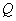 ) D.
) D. 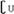 ( ( 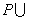
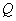 )
)
2.用反证法证实命题:若P则q ,其第一步是反设命题的结论不成立,这个命题正确的反设是( )
A.若P则非q B.若非P则q C.非P D.非q
3、已知点 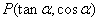 在第三象限, 则角
在第三象限, 则角 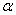 的终边在( ).
的终边在( ).
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
4.已知 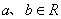 ,集合
,集合  表示把集合M中的元素x映射到集合N中仍为x,则a b的值为( )
表示把集合M中的元素x映射到集合N中仍为x,则a b的值为( )
A.-1 B.0 C.1 D. 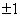
5.设a<0,角α的终边经过点P(-3a,4a),那么 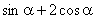 的值等于( )
的值等于( )
A. 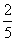 B. -
B. - 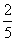 C.
C.  D. -
D. - 
6. 若关于x的方程4cos x-cos 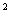 \* MERGEFORMAT
x m-3=0恒有实数解,则实数m的取值范围是( )
\* MERGEFORMAT
x m-3=0恒有实数解,则实数m的取值范围是( )
A.[-1, 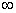 \* MERGEFORMAT
] B.[-1,8] C. [0,5] D. [0,8]
\* MERGEFORMAT
] B.[-1,8] C. [0,5] D. [0,8]
7、将函数y= 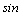 (
( 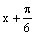 )(
)( 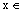 R)的图象上所有的点向左平行移动
R)的图象上所有的点向左平行移动 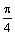 个单位长度,再把图像上各点的横坐标扩大到原来的2倍(纵坐标不变),则所得到的图象的解析式为( )
个单位长度,再把图像上各点的横坐标扩大到原来的2倍(纵坐标不变),则所得到的图象的解析式为( )
A.  (
( 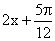 )(
)( 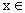 R) B.
R) B.  (
(  )(
)( 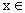 R)
R)
C.  (
( 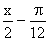 )(
)( 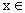 R) D.
R) D.  (
( 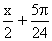 )(
)( 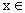 R)
R)
8.数列 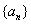 中,已知对任意正整数
中,已知对任意正整数 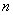 ,
,  ,则
,则 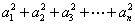 等于( )
等于( )
A.(2n-1)2 B. 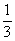 (2n-1) C.
(2n-1) C. 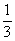 (4n-1) D.4n-1
(4n-1) D.4n-1
9.2002年8月在北京召开的国际数学家大会,会标是我国以古代数学家赵爽的弦图为基础设计的.弦图是由四个全等直角三角形与一个小正方形拼成的一个大正方形(如图).假如小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为  ,
, 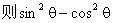 的值等于( )
的值等于( )
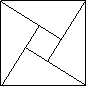 A.1 B. A.1 B. 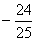
C. 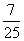 D.-
D.- 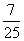
10.对于函数 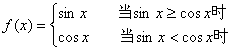 给出下列四个命题:( )
给出下列四个命题:( )
①该函数的值域为[-1,1]
②当且仅当 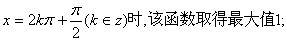
③该函数是以π为最小正周期的周期函数;
④当且仅当 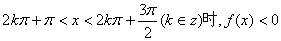
上述命题中错误命题的个数为
A.1 B.2 C.3 D.4
第II卷(非选择题 共50分)
11.半径为2,弦长也为2的扇形的面积为 。
12. 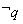 的值是
的值是
13.等差数列{an}中,若S10=15,则a1+a4+a7+a10=
14.已知tanα、tanβ是方程x2 3 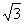 x 4=0的两个根,且α、β∈(-
x 4=0的两个根,且α、β∈(- 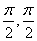 ),则α β的值是
),则α β的值是
15读下列命题,请把正确命题的序号都填在横线上 .
①已知命题 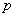 与命题
与命题 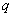 ,若
,若 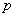 是
是 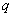 的充分不必要条件,则
的充分不必要条件,则 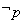 是
是 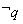 的充分不必要条件;
的充分不必要条件;
②若函数 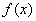 对定义域中的
对定义域中的 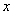 总有
总有 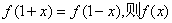 是奇函数;
是奇函数;
③函数  的图象关于点(-1,-2)成中心对称;
的图象关于点(-1,-2)成中心对称;
④已知f(x)是R上的函数,且满足f(x 2)= f(x),当x 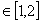 时,f(x)=
时,f(x)= 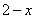 ,
,
则 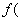 2007.5)的值为0.5.
2007.5)的值为0.5.
|
1
2 2
3 4 3
4 7 7 4
5 11 14 11 5 | | 16.如右图,它满足
①第n行首尾两数均为n
②表中的递推关系如杨辉三角,
则第n行(n≥2)的第二个数是
17已知A 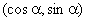 ,
, 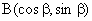 是单位圆上的两点,且
是单位圆上的两点,且 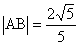 ,
,
(1) 求 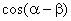 的值
的值
(2) (2)设 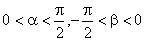 ,且
,且 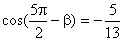 ,
,
求 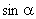 的值
的值
18.(本小题满分12分)
.设数列{an}的前n项和为Sn=n2,{bn}为等比数列,且a1=b1,b2(a2-a1)=b1
(1)求数列{an},{bn}的通项公式;
(2)设 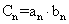 ,求数列
,求数列 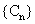 的前n项和Tn
的前n项和Tn
19.已知函数f(x)=acos2x-asinxcosx(a∈R)
(Ⅰ)若 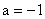 ,求f(x)在R上的单调递增区间;
,求f(x)在R上的单调递增区间;
(Ⅱ)若x∈[0, 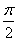 \* MERGEFORMAT
],f(x)的最小值为1-
\* MERGEFORMAT
],f(x)的最小值为1- 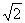 \* MERGEFORMAT
,试确定a的值.
\* MERGEFORMAT
,试确定a的值.
20(本小题满分13分) 已知二次函数f(x)=x2+bx+1(b∈R)满足f(-1)=f(3)
(1)求b的值;
(2)当x>1时,求f(x)的反函数f-1(x);
(3)对于(2)中的f-1(x),假如f-1(x)>m(m- EQ \r(x))在[ EQ \f(1,4), EQ \f(1,2)]上恒成立,求实数m的取值范围.
21、(本小题满分12分)
已知二次函数 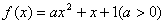 的图象与
的图象与 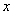 轴交点的横坐标分别为
轴交点的横坐标分别为 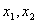 。
。
(1) 证实 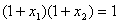 ;
; 
(2) 证实  ;
;
(3) 若 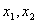 满足不等式
满足不等式 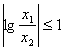 ,试求
,试求 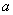 的取值范围。
的取值范围。
22.(本小题满分12分)
已知函数 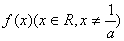 满足
满足  ,
, 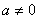 ,
, 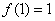 ;且使
;且使 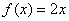 成立的实数
成立的实数 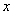 只有一个。
只有一个。
(Ⅰ)求函数 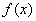 的表达式;
的表达式;
(Ⅱ)若数列 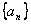 满足
满足 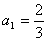 ,
, 
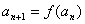 ,
, 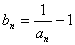 ,
, 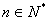 ,证实数列
,证实数列  是等比数列,并求出
是等比数列,并求出  的通项公式;
的通项公式;
(Ⅲ)在(Ⅱ)的条件下,证实: 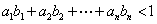 ,
, 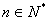 。
。
参考答案
1.A 2.D 3.B 4.C 5.A 6.D 7.B 8.C 9.D 10.C
11.  12.-
12.- 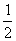 13. 6 14.
13. 6 14. 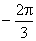 15.③④ 16.
15.③④ 16. 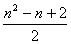
17解:(1)由题知 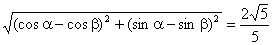 …………..2分
…………..2分
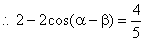 ,所以
,所以  …………..4分
…………..4分
(2) 
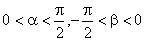 ,
, 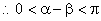 ,又
,又  ,
, 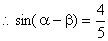 ………….7分
………….7分
而 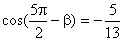 则
则  ,
, 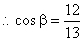 …………..10分
…………..10分
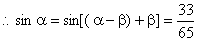 …………..13分
…………..13分
18.解:( = 1 \* ROMAN I) 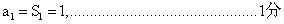
当 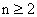 时,
时, 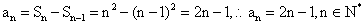 ……..3分
……..3分
∵ 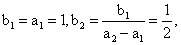 又
又 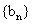 为等比数列,
为等比数列, 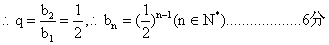
( = 2 \* ROMAN II) 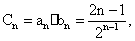 ①
①
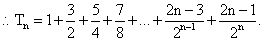 ②…………………..9分
②…………………..9分
①-②得, 
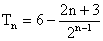 ……………13分
……………13分
19.解(Ⅰ)f(x)= 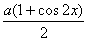 \* MERGEFORMAT
-
\* MERGEFORMAT
- 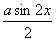 \* MERGEFORMAT
…………2分
\* MERGEFORMAT
…………2分
= 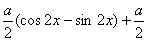 \* MERGEFORMAT
,∵
\* MERGEFORMAT
,∵ 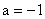 ,∴f(x)=
,∴f(x)= 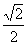 \* MERGEFORMAT
sin(2x-
\* MERGEFORMAT
sin(2x- 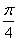 \* MERGEFORMAT
)-
\* MERGEFORMAT
)- 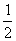 \* MERGEFORMAT
…………4分
\* MERGEFORMAT
…………4分
当2kπ- 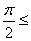 \* MERGEFORMAT
2x-
\* MERGEFORMAT
2x- 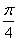 \* MERGEFORMAT
≤2kπ
\* MERGEFORMAT
≤2kπ 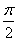 \* MERGEFORMAT
(k∈Z),即x∈[kπ-
\* MERGEFORMAT
(k∈Z),即x∈[kπ- 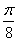 \* MERGEFORMAT
,kπ
\* MERGEFORMAT
,kπ 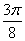 \* MERGEFORMAT
](k∈Z)时,函数单调递增。 ……6分 (没写区间或k∈Z扣1分)
\* MERGEFORMAT
](k∈Z)时,函数单调递增。 ……6分 (没写区间或k∈Z扣1分)
(Ⅱ)f(x)= 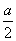 \* MERGEFORMAT
(cos2x-sin2x)
\* MERGEFORMAT
(cos2x-sin2x) 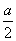 \* MERGEFORMAT
=
\* MERGEFORMAT
= 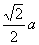 \* MERGEFORMAT
cos(2x
\* MERGEFORMAT
cos(2x 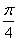 \* MERGEFORMAT
)
\* MERGEFORMAT
) 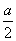 \* MERGEFORMAT
…………7分
\* MERGEFORMAT
…………7分
∵x∈[0, 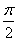 \* MERGEFORMAT
],∴
\* MERGEFORMAT
],∴ 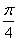 \* MERGEFORMAT
≤2x≤
\* MERGEFORMAT
≤2x≤ 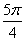 \* MERGEFORMAT
,得-1≤cos(2x
\* MERGEFORMAT
,得-1≤cos(2x 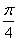 \* MERGEFORMAT
)≤
\* MERGEFORMAT
)≤ 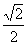 \* MERGEFORMAT
…………9
\* MERGEFORMAT
…………9
当a=0时,f(x)=0,不合题意
当a>0时,f(x) 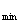 \* MERGEFORMAT
=-
\* MERGEFORMAT
=-  \* MERGEFORMAT
,得a=2…………11分
\* MERGEFORMAT
,得a=2…………11分
当a<0时,f(x) 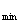 \* MERGEFORMAT
=
\* MERGEFORMAT
= 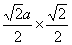 \* MERGEFORMAT
\* MERGEFORMAT
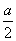 \* MERGEFORMAT
=1-
\* MERGEFORMAT
=1- 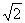 \* MERGEFORMAT
,得a=1-
\* MERGEFORMAT
,得a=1- 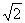 \* MERGEFORMAT
∴a=2或a=1-
\* MERGEFORMAT
∴a=2或a=1- 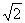 \* MERGEFORMAT
…………13分
\* MERGEFORMAT
…………13分
20、解:(1)∵f(-1)=f(3),∴1-b+1=9+3b+1
解得b=-2.(或利用对称性求解) ……3分
(2)由(1),记y=f(x)=x2-2x+1 ∵当x>1时,y=(x-1)2(y>0)∴x-1= EQ \r(y),即x=1+ EQ \r(y)
∴y=f-1(x)=1+ EQ \r(x) ……7'分
(3)∵f-1(x)>m(m- EQ \r(x)),x∈[ EQ \f(1,4), EQ \f(1,2)]∴1+ EQ \r(x)>m(m- EQ \r(x))上式对一切 EQ \f(1,4)≤x≤ EQ \f(1,2)的x的值恒成立
设t= EQ \r(x),则 EQ \f(1,2)≤t≤ EQ \f(\r(2),2)且g(t)=(1+m)(t-m+1)=(1+m)t-(m-1)(m+1),t∈[ EQ \f(1,2), EQ \f(\r(2),2)] ……9分
则g(t)为t的一次函数∵g(t)>0在t∈[ EQ \f(1,2), EQ \f(\r(2),2)]上恒成立
只需 EQ \b\lc\{(\a\al(g(\f(1,2))=(1+m)(\f(1,2)-m+1)>0,g(\f(\r(2),2))=(1+m)(\f(\r(2),2)-m+1)>0))解得-1<m< EQ \f(3,2) ……12分
∴m的取值范围是-1<m< EQ \f(3,2) ……13分
21、解(1)由题意知, 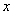 1`
1` 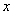 2是关于
2是关于 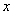 的一元二次方程
的一元二次方程 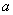
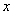
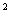
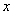 1=0有实数根,
1=0有实数根,
∴ 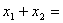 -
- 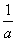 ,
, 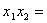
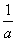 .∴
.∴ 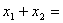
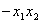
∴ 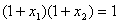 。。。。。。。。。。①…………3分
。。。。。。。。。。①…………3分
(2)证实:由于关于 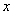 一元二次方程
一元二次方程 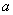
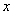
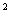
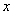 1=0有实数根
1=0有实数根 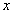 1,
1, 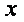 2,故有
2,故有
a﹥0且△=1-4a≥0. …………4分
∴0<a≤ 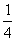 . ∴
. ∴ 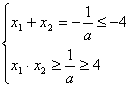 …………5分
…………5分
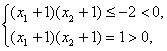
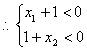 即
即  得证。…………7分
得证。…………7分
(4) 解:由 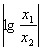 ≤1
≤1 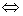 -1≤
-1≤ 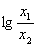 ≤1
≤1 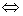
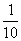 ≤
≤ 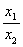 ≤10,由①得
≤10,由①得 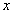 1=
1= 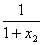
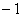 =
= 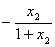 。∴
。∴ 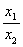 =-
=- 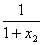 。
。
∴ 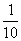 ≤-
≤- 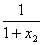 ≤10,
≤10,  ≤-
≤- 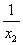 ≤
≤  。∴a=
。∴a= 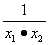 =-
=-  =-
=- 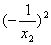 (
( 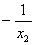 )=
)= 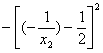
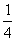 ,
,
当 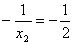 时,a取最大值为
时,a取最大值为 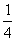 。
。
当 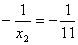 或
或 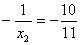 时,a取最小值
时,a取最小值 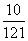 。
。
故a的取值范围是[ 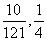 ]。…………12分
]。…………12分
22.(解:(Ⅰ)由  ,
, 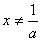 ,
, 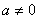 ,得
,得 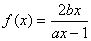 .………1分
.………1分
由 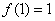 ,得
,得 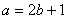 .……………………………………………………………2分
.……………………………………………………………2分
由 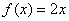 只有一解,即
只有一解,即  ,也就是
,也就是 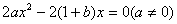 只有一解,
只有一解,
∴ 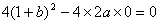
∴ 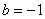 .…………………………………………………………………………………3分
.…………………………………………………………………………………3分
∴ 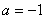 .故
.故 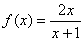 .……………………………………………………………4分
.……………………………………………………………4分
(Ⅱ)∵  ,
, 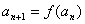 ,∴
,∴ 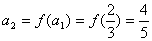 ,
,
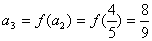 ,
, 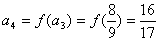 ,……………………………5分
,……………………………5分
猜想, 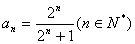 .……………………………………………………………6分
.……………………………………………………………6分
下面用数学归纳法证实:
10 当n=1时,左边= 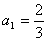 ,右边=
,右边= 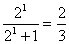 ,∴命题成立. ……………………7分
,∴命题成立. ……………………7分
20 假设n=k时,命题成立,即 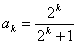 ;当 n=k 1时,
;当 n=k 1时, 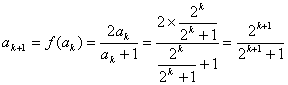 ,
,
∴当 n=k 1时,命题成立. ……………………………………………………………8分
由10,20可得,当 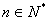 时,有
时,有 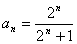 .∵
.∵ 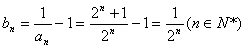 ,∴
,∴ 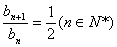
∴  是首项为
是首项为 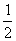 ,公比为
,公比为 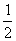 的等比数列,其通项公式为
的等比数列,其通项公式为 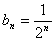 .……………9分
.……………9分
(Ⅲ)∵ 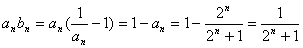 ,
,
∴ 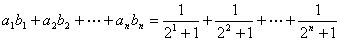 …………………………10分
…………………………10分
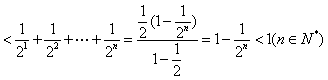 .……………………………12分
.……………………………12分
|